Compilers Questions and Answers – Minimization of DFA – 2

This set of Compilers Multiple Choice Questions & Answers (MCQs) focuses on “Minimization of DFA – 2”.

1. The language accepted by this DFA is?

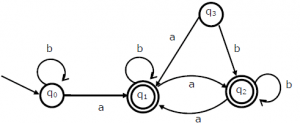
a) b*ab*ab*ab*
b) (a+b)*
c) b*a(a+b)*
d) b*ab*ab*
View Answer

2. The minimum state automation equivalent to the below FSA has the following number of states?

a) 1
b) 2
c) 3
d) 4
View Answer

Answer: b
Explanation: State q0 can be omitted because it takes the same input as state q1 hence by removing q0 nothing changes.

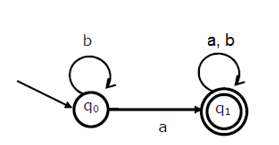
Following is equivalent FSA with 2 states.

3. Which one of the following is TRUE?
a) The language L={a^n b^n |n>0 } is regular
b) The language L={a^n |n is prime } is regular
c) The language L={w|w has 3k+1 b’s for some k } is regular
d) None of the mentioned
View Answer

4.
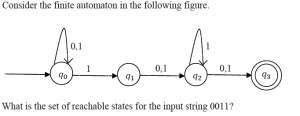
a) q0, q1,q2
b) q0,q1
c) q0,q1,q2,q3
d) q3
View Answer

5. Which of the regular expressions given below represent the following DFA?

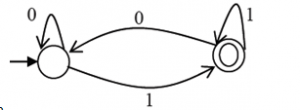
I) 0*1(1+00*1)*
II) 0*1*1+11*0*1
III) (0+1)*1
a) I and II only
b) I and III only
c) II and III only
d) I II III
View Answer

6. Let L1 = {w ∈ {0,1}∗ | w has at least as many occurrences of (110)’s as (011)’s}.
Let L2 = { ∈ {0,1}∗ | w has at least as many occurrences of (000)’s as (111)’s}.
Which one of the following is TRUE?
a) L1 is regular but not L2
b) L2 is regular
c) L1 and L2 are regular
d) Neither of them are regular
View Answer

7. The length of the shortest string NOT in the language (over Σ = {a, b}) of the following regular expression is _____________
a*b*(ba)*a*
a) 2
b) 3
c) 4
d) 5
View Answer

8. Consider the machine M: The language recognized by M is :

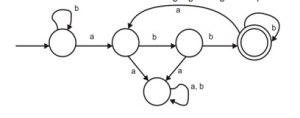
a) {w ∈ {a, b}* / every a in w is followed by ex¬actly two b’s}
b) {w ∈ {a, b}* every a in w is followed by at least two b’}
c) {w ∈ {a, b}* w contains the substring ‘abb’}
d) {w ∈ {a, b}* w does not contain ‘aa’ as a substring}
View Answer

9. Consider the following deterministic finite state automaton M.

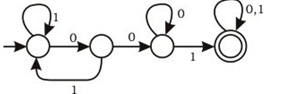
S denotes the set of seven bit in which the 1st ,4th and last bits are 1. The number of strings that are accepted by M is
a) 1
b) 5
c) 7
d) 8
View Answer

Sanfoundry Global Education & Learning Series – Compilers.

To practice all areas of Compilers, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]