Compilers Questions and Answers – Minimization of DFA – 1

This set of Compilers Multiple Choice Questions & Answers (MCQs) focuses on “Minimization of DFA – 1”.

1. Consider the languages L1 = and L2 = {a}. Which one of the following represents L1 L2* U L1*?
a) €
b) a*
c) All of the mentioned
d) None of the mentioned
View Answer

2. Choose the correct statement for the following daigram.

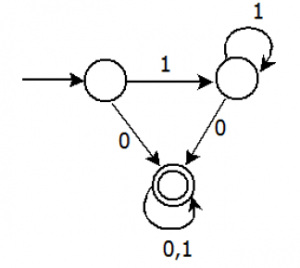
a) For the language accepted by A which is also a minimal DFA
b) A accepts all strings over {0,1} of length at least 2
c) All of the mentioned
d) None of the mentioned
View Answer

3. Given the language L = {ab, aa, baa}, which of the following strings are in L*?

1) abaabaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa 

a) 1, 2, 3
b) 2, 3, 4
c) 1, 2, 4
d) 1, 3, 4
View Answer

4. W hat is the complement of the language accepted by the NFA shown below?

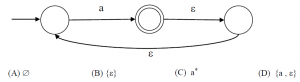
a) A,B
b) B
c) C
d) D,C
View Answer

5. A deterministic finite automation (DFA)D with alphabet {a,b} is given below Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?

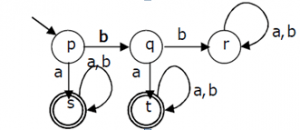
a)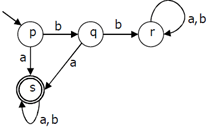
b)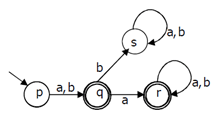
c)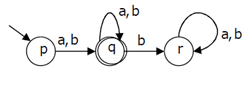
d)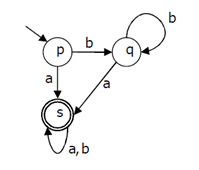
View Answer

6. Let w be any string of length n is {0,1}*. Let L be the set of all substring of w.
State the minimum number of states in a NDFA that accepts L?

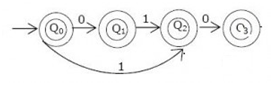
a) n – 1
b) n
c) n + 1
d) 2n – 1
View Answer

7. Which one of the following languages over the alphabet {0,1} is described by the regular expression?

(0+1)*0(0+1)*0(0+1)*

a) String with substring 00
b) String with at most two 0’s
c) String containg at least two 0’s
d) None of the mentioned
View Answer

8. Which one of the following is FALSE?
a) Every NFA can be converted to DFA
b) Every subset of a recursively enumerable set is recursive
c) All of the mentioned
d) None of the mentioned
View Answer

9. Match the following NFAs with the regular expressions.

 1. ϵ + 0(01*1 + 00) * 01*
 2. ϵ + 0(10 *1 + 00) * 0
 3. ϵ + 0(10 *1 + 10) *1
 4. ϵ + 0(10 *1 + 10) *10 *

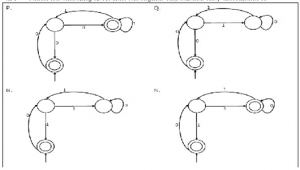
a) P-2, Q-1, R-3, S-4
b) P-1, Q-3, R-2, S-4
c) P-1, Q-2, R-3, S-4
d) P-3, Q-2, R-1, S-4
View Answer

10. Which of the following are regular sets?

I. { an b2m | n>=0, m>=0}
II. {an bm |n=2m}
III. {an bm | n!= m}
IV {xcy |x,y€{a,b)*}

a) I and IV
b) I and III
c) I and only
d) IV
View Answer

Sanfoundry Global Education & Learning Series – Compilers.

To practice all areas of Compilers, here is complete set of 1000+ Multiple Choice Questions and Answers.