Physical Chemistry Questions and Answers – Quantum Theory – Rigid Rotor

This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Quantum Theory – Rigid Rotor”.

1. What is the moment of inertia I of a body mass m rotating about a radius r?
a) I = mr²
b) I = mr
c) I = m² r
d) I = \(\frac{m}{r^2}\)
View Answer

2. What is the mathematical definition of angular momentum L for a classical particle in terms of moment of inertia I and angular frequency ω?
a) L = I²ω
b) L = Iω²
c) L = \(\frac{I}{\omega}\)
d) L = Iω
View Answer

3. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{3}{4\pi}}\) e^iΦ – \(\frac{i}{\sqrt {4\pi}}\) e^-2iΦ. Normalized eigenfunctions for a particle on a ring are given by φ(Φ) = \(\frac{1}{\sqrt {2\pi}}\) e^imΦ; m = 0, 1, 2… What should this wavefunction be divided by for normalization?
a) 2
b) √2
c) \(\frac{1}{2\pi}\)
d) \(\frac{1}{\sqrt 2}\)
View Answer

4. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{3}{4\pi}}\) e^iΦ – \(\frac{i}{\sqrt {4\pi}}\) e^-2iΦ. Normalized eigenfunctions for a particle on a ring are given by φ(Φ) = \(\frac{1}{\sqrt {2\pi}}\) e^imΦ; m = 0, 1, 2… What is the expectation value of energy for this system?
a) < E > = \(\frac{\hbar^2}{2\mu r^2}\)
b) < E > = \(\frac{7\hbar^2}{8\mu r^2}\)
c) < E > = 0
d) < E > = \(\frac{\hbar^2}{4\pi\mu r^2}\)
View Answer

5. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{3}{4\pi}}\) e^iΦ – \(\frac{i}{\sqrt {4\pi}}\) e^-2iΦ. Is this wavefunction an eigenfunction of the angular momentum operator L_z = -iη\(\frac{\partial}{\partial\varphi}\)?
a) Yes, with eigenvalue \(\frac{4\pi}{3}\)
b) Yes, with eigenvalue \(\frac{2\pi}{3}\)
c) Yes, with eigenvalue \(\sqrt{4\pi/3}\)
d) No, it is not an eigenfunction of the given operator
View Answer

6. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{3}{4\pi}}\) e^iΦ – \(\frac{i}{\sqrt {4\pi}}\) e^-2iΦ. What is the expectation value of angular momentum in the z-direction for this state?
a) < L_z > = \(\frac{\hbar}{4}\)
b) < L_z > = \(\frac{\hbar}{4\pi^2}\)
c) < L_z > = \(\frac{7\hbar}{8}\)
d) < L_z > = \(\frac{\hbar^2}{4}\)
View Answer

7. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{1}{8\pi}}\) e^iΦ – \(\frac{i}{2\sqrt{\pi}}\) e^-3iΦ + \(\frac{1}{2\sqrt {2\pi}}\) e^i5Φ. Normalized eigenfunctions for a particle on a ring are given by φ(Φ) = \(\frac{1}{\sqrt {2\pi}}\) e^imΦ; m = 0, 1, 2… What should this function be divided by for normalization?
a) 1
b) √2
c) 2√2
d) √3
View Answer

8. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{1}{8\pi}}\) e^iΦ – \(\frac{i}{2\sqrt \pi}\) e^-3iΦ + \(\frac{1}{2\sqrt {2\pi}}\) e^i5Φ. What is the expectation of energy in this superposition state?
a) < E > = \(\frac{\hbar^2}{2\mu r^2}\)
b) < E > = \(\frac{\hbar^2}{\mu r^2}\)
c) < E > = \(\frac{5\hbar^2}{2\mu r^2}\)
d) < E > = \(\frac{11\hbar^2}{2\mu r^2}\)
View Answer

9. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{1}{8\pi}}\) e^iΦ – \(\frac{i}{2\sqrt \pi}\) e^-3iΦ + \(\frac{1}{2\sqrt {2\pi}}\) e^i5Φ. Is this wavefunction an eigenfunction of the angular momentum operator L_z = -iη\(\frac{\partial}{\partial\varphi}\)?
a) Yes, with eigenvalue \(\frac{4\pi}{3}\)
b) Yes, with eigenvalue \(\frac{2\pi}{3}\)
c) Yes, with eigenvalue \(\sqrt{4\pi/3}\)
d) No, it is not an eigenfunction of the given operator
View Answer

10. A particle on a ring exists in a superposition state: φ(Φ) = \(\sqrt{\frac{1}{8\pi}}\) e^iΦ – \(\frac{i}{2\sqrt \pi}\) e^-3iΦ + \(\frac{1}{2\sqrt {2\pi}}\) e^i5Φ. What is the expectation of energy in this superposition state?
a) < L_z > = \(\frac{\hbar}{4}\)
b) < L_z > = \(\frac{\hbar}{4\pi^2}\)
c) < L_z > = \(\frac{7\hbar}{8}\)
d) < L_z > = 0
View Answer

11. A wavefunction is given by φ(x) = \((\frac{4\alpha^3}{\pi})^{1/4} xe^{\frac{-\alpha x^2}{2}}\). Is this function odd or even?
a) Odd, because φ(-x) = -φ(x)
b) Odd, because φ(x) = -φ(x)
c) Even, because φ(-x) = -φ(x)
d) Even, because φ(-x) = φ(x)
View Answer

12. A wavefunction is given by φ(x) = \((\frac{4\alpha^3}{\pi})^{1/4} xe^{\frac{-\alpha x^2}{2}}\). Is this function acceptable according to the Born conditions?
a) Yes, because the function and its derivatives are continuous and finite everywhere
b) No, because the function and its derivatives are continuous and finite everywhere
c) Yes, because the function and its derivatives are neither continuous nor finite everywhere
d) No, because the function and its derivatives are neither continuous nor finite everywhere
View Answer

Answer: a
Explanation: The given wavefunction is continuous and finite and so are its derivatives. A plot of the function is included below:

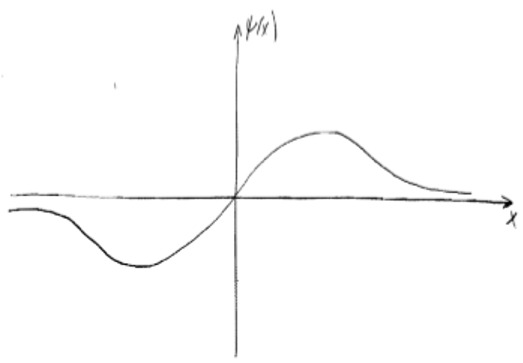
13. A wavefunction is given by φ(x) = \((\frac{4\alpha^3}{\pi})\)^1/4 \(xe^{\frac{-\alpha x^2}{2}}\). Which stationary state does this function describe?
a) Ground state
b) First excited state
c) Second excited state
d) Third excited state
View Answer

14. What is an element of differential volume dv in spherical coordinates?
a) dv = r² sin ⁡θ drd⁡θ
b) dv = drd⁡θdΦ
c) dv = r² drd⁡θdΦ
d) dv = r² sin⁡θ drd⁡θdΦ
What is an element of differential volume dv in spherical coordinates?
View Answer

15. By what factor does the energy of a rigid rotor change if the moment of inertia of a particle on a sphere is increased by a factor of 2?
a) Decreases by a factor of 2
b) Increases by a factor of 2
c) Stays the same
d) Increases by a factor of 4
What is an element of differential volume dv in spherical coordinates?
View Answer

Sanfoundry Global Education & Learning Series – Physical Chemistry.

To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]