This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Particle in a One-Dimension Box”.
1. What is the potential energy term in the Schrodinger equation for a particle outside the boundaries of a confined one-dimensional box?
a) V(x) = ∞
b) V(x) = 0
c) V(x) = -∞
d) V(x) = 1
View Answer
Explanation: Potential energy outside the boundaries of a box is infinite because the potential has no limits. This goes from 0 inside the box to infinite outside. The mere definition of a particle in a box makes the potential energy outside a box to be infinite because it is boundless.
2. What is the solution to the Schrodinger equation for a particle lying outside the boundaries of a confined one – dimensional box?
a) φ = ∞
b) φ = 0
c) φ = -∞
d) φ = 1
View Answer
Explanation: Since potential outside the box is infinite, the only way to satisfy the Schrodinger’s equation would be if the wavefunction is zero. This would satisfy the boundary conditions as well as the equation. Hence, the wavefunction does not exist outside the confines of the box.
3. What is the boundary condition for the wavefunction at x=0 and x=a to avoid a discontinuity of the wavefunction?
a) φ = ∞
b) φ = 0
c) φ = -∞
d) φ = 1
View Answer
Explanation: Since the potential outside the box is infinite, the only way to satisfy the Schrodinger’s equation would be if the wavefunction outside the box is zero. Since this is the case, the wavefunction on the boundary must be zero as well to satisfy the boundary conditions and avoid discontinuity.
4. What is the nature of the energy dependence on position in the box once the boundary conditions are satisfied?
a) Energy is neither continuous or quantized, its value is arbitrary
b) Energy is continuous
c) Energy is quantized
d) Quantized or discreet nature of energy depends on the medium of the box
View Answer
Explanation: Boundary conditions can only be satisfied if the energy levels are quantized, i.e. discrete. This gives separates states, or energy levels, rather than a band.
5. The Schrodinger equation for a particle within the box simplifies to: \(\frac{-\hbar^2}{2m} \frac{d^2\varphi}{dx^2}\) = Eφ. What form of the wavefunction satisfies this equation and all other conditions for a particle in a box?
a) φ(x) = A cos(kx)
b) φ(x) = ekx
c) φ(x) = 0
d) φ(x) = A cos (kx) + B sin(kx)
View Answer
Explanation: Alternating sin and cosine functions satisfy the above differential equation. Having either one of sin or cosine is incorrect because differentiation several times does not account for changes in sign. Although φ(x) = 0 satisfies this equation, the wavefunction inside the box is well defined and thus cannot be zero.
6. What is the mathematical outcome of the boundary condition at x = a?
a) ka = nπ
b) k = eiπa
c) k = A cos(kx) + B sin(kx)
d) k = A cos(sin(kx))
View Answer
Explanation: The boundary condition at x = a forces the wavefunction at this boundary to be φ(x) = 0. This gives sin ka = 0 — → ka = nπ since the sin function is has a period of π.
7. Given ka = nπ and k = \(\frac{\sqrt{2mE}}{\hbar}\), what is the quantized energy for a particle in the box?
a) En = \(\frac{h^2}{16ma^2}\)
b) En = \(\frac{1}{8ma^2}\)
c) En = \(\frac{h^2 n^2}{5m}\)
d) En = \(\frac{h^2 n^2}{8ma^2}\)
View Answer
Explanation: Equating the two k’s gives: \(\frac{n\pi}{a}=\frac{\sqrt{2mE}}{\hbar}\) — → writing ħ as \(\frac{h}{2\pi}\) and solving for E gives En = \(\frac{h^2 n^2}{8ma^2}\).
9. A particle in a box exists in a superposition state: ψ(x, t) = ψ1(x, t) + √3 ψ2(x, t), where ψ1(x, t) and ψ2(x, t) are stationary states with quantum numbers n=1 and n=2 respectively. By what number should the overall wavefunction ψ(x, t) be divided by for normalization?
a) 2
b) 1
c) 4
d) ½
View Answer
Explanation: A wavefunction is considered normalized if the sum of the square of individual wavefunction coefficients equals to one. In this case, Σn|cn|2 = 12 + (√3)2 = 2. Hence the wavefunction is not normalized. To normalize the overall wavefunction, ψ(x, t) should be divided by 2 to make sure the sum of coefficients equals to one. Dividing the wavefunction by one means it is already normalized (which is not in this case) and dividing it by 4 or ½ does not satisfy the normalization criteria.
Overall normalized wavefunction: ψ(x, t) = \(\frac{\psi_1}{2}\)(x, t) + \(\frac{\sqrt{3}}{2}\) ψ2(x, t).
10. If the size of the box increases by a factor of 2, how does it affect the energy?
a) Increases by a factor of 2
b) Decreases by a factor of 2
c) Increases by a factor of 4
d) Decreases by a factor of 4
View Answer
Explanation: Since En = \(\frac{h^2 n^2}{8ma^2}\), increasing the size of the box by 2 will decrease the energy by 4 because of inverse square proportionality. This implies that a bigger box drastically lowers the energy of the system and vice versa.
11. A quantum particle moving from left to right approaches a step barrier with energy E < |V0| (shown below). What is the wavefunction form for this particle traveling inside the barrier?
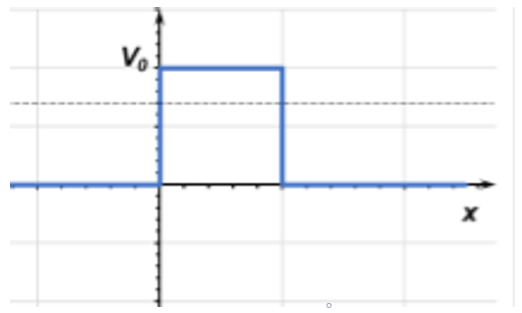
a) φ(x) = Ae-kIIx, where kII = \(\frac{\sqrt{2m(V_0-E)}}{\hbar}\)
b) φ(x) = AekIx + Be-kIx, where kI = \(\frac{\sqrt{2mE}}{\hbar}\)
c) φ(x) = Ae-kIx, where kI = \(\frac{\sqrt{2mV_0}}{\hbar}\)
d) φ(x) = AekIIx, where kII = \(\frac{\sqrt{2mV_0}}{\hbar}\)
View Answer
Explanation: Since the energy is lower than the step barrier, the wavefunction will decay exponentially in proportion to the difference in energy between the particle and the step. This phenomenon is known as quantum tunneling and is a property that only occurs in quantum mechanics. Classical mechanics forbids tunneling in any form.
12. A quantum particle moving from left to right approaches a well with energy E < |V0| (shown below). What is the wavefunction form for this particle traveling inside the barrier?
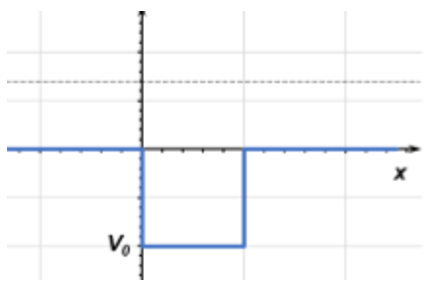
a) φ(x) = Ae-kIIx, where kII = \(\frac{\sqrt{2m(V_0+E)}}{\hbar}\)
b) φ(x) = AekIx + Be-kIx, where kI = \(\frac{\sqrt{2m(E+V_0)}}{\hbar}\)
c) φ(x) = Ae-kIx, where kI = \(\frac{\sqrt{2mV_o}}{\hbar}\)
d) φ(x) = AekIIx, where kII = \(\frac{\sqrt{2mV_o}}{\hbar}\)
View Answer
Explanation: Since the energy of the particle is greater than the well, it will continue moving as a wave with an addition to the energy term. This is the reverse of quantum tunneling and behaves the same way in the opposite direction.
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
