This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Quantum Theory – Tunneling and Reflection”.
1. What is the quantum mechanical phenomenon in which a wavefunction can be nonzero in a classically forbidden region?
a) Refraction
b) Reflection
c) Tunneling
d) Radiation
View Answer
Explanation: Tunneling is the phenomenon in which a wavefunction can be non-zero in a classically forbidden region. A particle has a finite probability to cross an energy barrier even if it does not possess that much energy. In classical mechanics, there is no way by which a particle possessing 20 Joules of kinetic energy can cross a potential barrier of 25 Joules.
2. Amidst crossing a barrier of energy V > E (energy of the particle), what is the wavefunction solution of this particle?
a) φ = Aekx + Be-kx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
b) φ = Aekx + Be-kx, k = \(\sqrt{\frac{2mV}{\hbar^2}}\)
c) φ = Aekx + Be-kx, k = \(\sqrt{\frac{2m(V+E)}{\hbar^2}}\)
d) φ = A sin kx + B cos kx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
View Answer
Explanation: The Schrodinger equation is written as –\(\frac{\hbar^2}{2m} \frac{d^2}{dx^2}\) φ + Vφ = Eφ. Moving all variables to one end gives \(\frac{2m(V-E)}{\hbar^2}\) φ = k2 = \(\frac{d^2}{dx^2}\) φ. This has an exponential solution and is written as φ = Aekx + Be-kx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\).
3. What is the wavefunction form after the particle crosses the potential barrier?
a) φ = Fekx + Ge-kx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
b) φ = Fekx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
c) φ = Fe-ikx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
d) φ = Feikx, k = \(\sqrt{\frac{2m(V-E)}{\hbar^2}}\)
View Answer
Explanation: After crossing the barrier, the wavefunction oscillates, but with a smaller amplitude. This is true since the particle is incident from the left, hence no reflected wave.
4. A quantum particle moving from left to right approaches a step barrier with energy E < |V0| (shown below). What is the wavefunction form for this particle traveling inside the barrier?
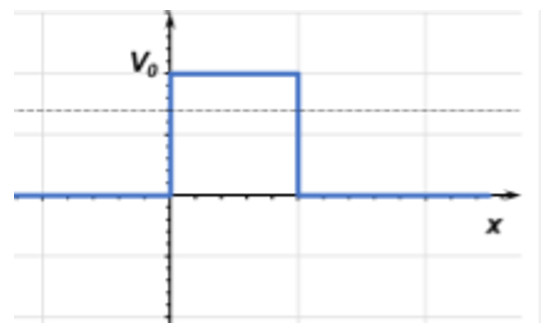
a) φ(x) = Ae-kIIx, where kII = \(\frac{\sqrt{2m(V_0 – E)}}{\hbar}\)
b) φ(x) = AekIx + Be-kIx, where kI = \(\frac{\sqrt{2mE}}{\hbar}\)
c) φ(x) = Ae-kIx, where kI = \(\frac{\sqrt{2mV_0}}{\hbar}\)
d) φ(x) = AekIIx, where kII = \(\frac{\sqrt{2mV_0}}{\hbar}\)
View Answer
Explanation: Since the energy is lower than the step barrier, the wavefunction will decay exponentially in proportion to the difference in energy between the particle and the step. This phenomenon is known as quantum tunneling and is a property that only occurs in quantum mechanics. Classical mechanics forbids tunneling in any form.
5. A quantum particle moving from left to right approaches a well with energy E < |V0| (shown below). What is the wavefunction form for this particle traveling inside the barrier?
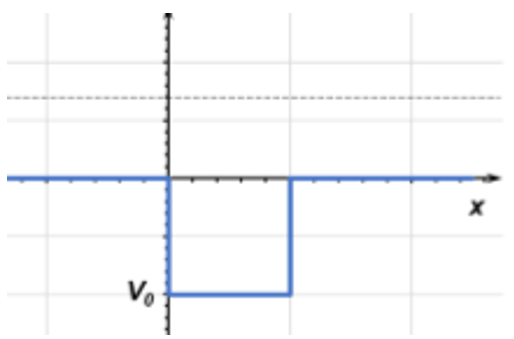
a) φ(x) = Ae-kIIx, where kII = \(\frac{\sqrt{2m(V_0 + E)}}{\hbar}\)
b) φ(x) = AekIx + Be-kIx, where kI = \(\frac{\sqrt{2m(E+V_0)}}{\hbar}\)
c) φ(x) = Ae-kIx, where kI = \(\frac{\sqrt{2mV_0}}{\hbar}\)
d) φ(x) = AekIIx, where kII = \(\frac{\sqrt{2mV_0}}{\hbar}\)
View Answer
Explanation: Since the energy of the particle is greater than the well, it will continue moving as a wave with an addition to the energy term. This is the reverse of quantum tunneling and behaves the same way in the opposite direction.
6. A particle of mass m is moving in the following potential (diagram shown below). What is the Schrodinger equation in the left most region?
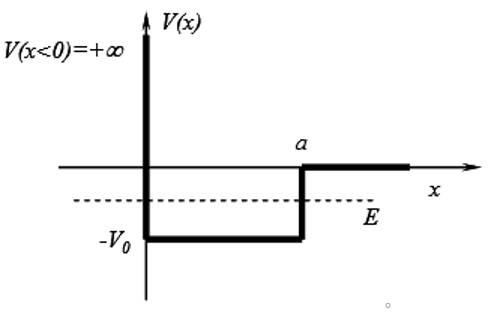
a) φ(x) = Aekx + Be-kx, where k = \(\sqrt{\frac{2m(V_0 + E)}{\hbar^2}}\)
b) φ(x) = Aekx + Be-kx, where k = \(\sqrt{\frac{2mV}{\hbar^2}}\)
c) φ(x) = Aekx + Be-kx, where k = \(\sqrt{\frac{2m(V + E)}{\hbar^2}}\)
d) φ = 0
View Answer
Explanation: The potential energy is infinite, hence the wavefunction must be zero to satisfy the Schrodinger equation. The wavefunction cannot exist in this region as it would have to go through an infinite potential.
7. A particle of mass m is moving in the following potential (diagram shown below). What is the Schrodinger equation in the middle region?

a) φ = A sin kx + B cos kx, k = \(\sqrt{\frac{2m(V_0 + E)}{\hbar^2}}\)
b) φ(x) = Aekx + Be-kx, where k = \(\sqrt{\frac{2mV}{\hbar^2}}\)
c) φ(x) = Aekx + Be-kx, where k = \(\sqrt{\frac{2m(V_0 + E)}{\hbar^2}}\)
d) φ = 0
View Answer
Explanation: The Schrodinger equation is written as –\(\frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)φ – V0φ = Eφ. Moving all variables to one end gives \(\frac{2m(V_0 + E)}{\hbar^2}\)φ = k2 = \(\frac{d^2}{dx^2}\)φ. This has a trigonometric solution and is written as φ = A sin kx + B cos kx, k = \(\sqrt{\frac{2m(V_0 + E)}{\hbar^2}}\).
8. A particle of mass m is moving in the following potential (diagram shown below). What is the Schrodinger equation in the right most region?

a) φ = A sin kx + B cos kx, k = \(\sqrt{\frac{2m(V_0 + E)}{\hbar^2}}\)
b) φ(x) = Aekx, k = \(\sqrt{\frac{2mV}{\hbar^2}}\)
c) φ(x) = Be-kx, k = \(\sqrt{\frac{-2mE}{\hbar^2}}\)
d) φ = 0
View Answer
Explanation: After the particle exits the potential well, its wavefunction decays exponentially. AT this point, the particle has zero energy and the wavefunction is asymptotic to the x axis.
9. A particle of mass m is moving in the following potential (diagram shown below). What is the boundary condition at x = 0?

a) φ(∞) = 0
b) φ(0) = ∞
c) φ(0) = 0
d) φ(∞) = ∞
View Answer
Explanation: at x = 0, the wavefunction must be 0 for the overall wavefunction to be continuous. This is because the wavefunction is 0 at values of x lesser than 0; to remain continuous this must remain true at x = 0 as well.
11. A particle of mass m is moving in the following potential (diagram shown below). What is the outcome of the boundary condition at x = 0?

a) Coefficient of cos(kx) = 0
b) Coefficient of sin(kx) = 0
c) The entire wavefunction equals to zero
d) The entire wavefunctions equals to infinity
View Answer
Explanation: Plugging x=0 in the equation φ = A sin kx + B cos kx and setting the wavefunction as 0 gives B = 0 as only the sin term can exist for the wavefunction being x at this point. This is true as cos(0) is not equal to zero.
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
