This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Variational Method – Set 2”.
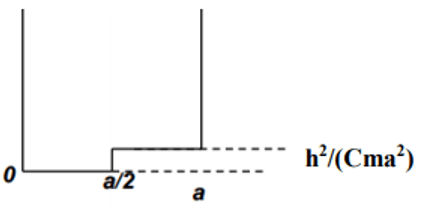
1. A particle of mass m in an infinite potential well is perturbed as shown in the figure below (C is an arbitrary constant). What is the unperturbed ground state energy?
a) E0 = 0
b) E0 = \(\frac{n^2 h^2}{2ma^2}\)
c) E0 = \(\frac{nh^2}{4\pi ma^2}\)
d) E0 = \(\frac{n^2 h}{4ma^2}\)
View Answer
Explanation: The ground state energy for the unperturbed box will be same as the ground state energy for a particle in a box. Although the perturbation will cause a change in energy states, the ground state will be same before this disturbance occurs. Hence, E0 = \(\frac{n^2 h^2}{2ma^2}\)
2. A particle of mass m in an infinite potential well is perturbed as shown in the figure below (C is an arbitrary constant). What is the first order energy shift (\(E_n^{(1)}\)) of the n state due to perturbation?

a) \(\frac{h^2}{2Cma^2}\)
b) \(\frac{n^2 h^2}{2ma^2}\)
c) 0
d) \(\frac{2C\pi^2 h^2}{ma^2}\)
View Answer
Explanation: Ground state wavefunction for a particle in a box is φ = \(\sqrt{\frac{2}{a}}sin \frac{n\pi x}{a}. E_n^{(1)}\) = \( \lt \varphi_{n}^{o}\)|H‘|\( \varphi_{n}^{0} \gt \) = \(\frac{2}{a} \frac{h^2}{Cma^2}\int_{\frac{a}{2}}^a\) sin2 \(\frac{n\pi x}{a}\) dx = \(\frac{h^2}{Cma^3}\)(\(\frac{a}{2} – \frac{a}{2n\pi}\)sin \(\frac{n\pi x}{a}\) (insert boundaries)) = \(\frac{h^2}{2Cma^2}\). Hence the shift in energy is given by this expression.
3. A particle of mass m in an infinite potential well is perturbed as shown in the figure below (C is an arbitrary constant). What is the range of C values for the perturbation validity?

a) C >> \(\frac{1}{n}\)
b) C >> n
c) C >> n2
d) C >> \(\frac{1}{n^2}\)
View Answer
Explanation: Ground state wavefunction for a particle in a box is φ = \(\sqrt{\frac{2}{a}}sin \frac{n\pi x}{a}. E_n^{(1)}\) = \( \lt \varphi_{n}^{o}\)|H‘|\(\varphi_{n}^{0} \gt\) = \(\frac{2}{a} \frac{h^2}{Cma^2}\int_{\frac{a}{2}}^a\) sin2 \(\frac{n\pi x}{a}\) dx = \(\frac{h^2}{Cma^3}\)(\(\frac{a}{2} – \frac{a}{2n\pi}\)sin \(\frac{n\pi x}{a}\) (insert boundaries)) = \(\frac{h^2}{2Cma^2}\). Perturbation is applicable for \(E_n^{(1)} \lt\lt E_n^{(0)} -\rightarrow \frac{h^2}{2Cma^2} \lt\lt \frac{n^2 h^2}{2Cma^2} -\rightarrow C \gt\gt \frac{1}{n^2}\).
4. What is the applicability for perturbation theory as an extension of the variational method?
a) \(E_{n-1}^{(1)} \gt\gt E_n^{(0)}\)
b) \(E_{n-1}^{(1)} \lt\lt E_{n+1}^{(0)}\)
c) \(E_{n}^{(1)} \gt\gt E_n^{(0)}\)
d) \(E_{n}^{(1)} \lt\lt E_n^{(0)}\)
View Answer
Explanation: Perturbation theory is only applicable for a small shift in energy. Hence, the n-order shift in energy must be much lesser than the ground state energy chosen.
5. What is an an-harmonic oscillator?
a) A harmonic oscillator in which radius tends to infinity as potential energy becomes infinite
b) A harmonic oscillator moving in the opposite direction
c) A harmonic oscillator with non-discreet energy levels
d) A harmonic oscillator with a perturbed potential energy
View Answer
Explanation: An an-harmonic oscillator has a disturbance energy which increases the Hamiltonian and its subsequent energy levels. This is different from the harmonic oscillator in the sense that the potential energy tends to zero (not infinity) as the radius tends to infinity. The potential thus converges at large values of radius.
6. An an-harmonic perturbation is given by V(x) = cx3 + dx4. What is the Hamiltonian for this system?
a) H = –\(\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac{1}{2}\)mω2x2 + cx3 + dx4
b) H = cx3 + dx4
c) H = 0
d) H = –\(\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac{1}{2}\)mω2x2
View Answer
Explanation: The Hamiltonian is the sum of all kinetic and potential energies. Here, the perturbation is included as it contributes to the energy of this system. This is the total Hamiltonian to be plugged into the Schrodinger equation to find energy eigenvalues for this system.
7. What are the eigenvalues to the unperturbed harmonic oscillator?
a) \(E_n^{(0)}\) = 0
b) \(E_n^{(0)}\) = \(\frac{n^2 h^2}{2ma^2}\)
c) \(E_n^{(0)}\) = (\(\frac{n+1}{2}\))ħω
d) \(E_n^{(0)}\) = (2πn)2ħω
View Answer
Explanation: The unperturbed harmonic oscillator has no disturbances hence the ground state energy will be same for a regular harmonic oscillator. The Hamiltonian for this is given by H = –\(\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac{1}{2}\)mω2x2. Plugging this into the Schrodinger equation will yield eigenvalues of \(E_n^{(0)}\) = (n + \(\frac{1}{2}\))ħω
8. How do interacting energy levels behave with respect to each other?
a) They attract each other
b) They repel each other
c) They split into smaller energy spacings
d) They increase degeneracy of respective states
View Answer
Explanation: Energy levels repel each other and cause a shift in spacing and different levels. In perturbation, the relative shift in energy caused by perturbation affects energy spacings too. Energy levels naturally repel each other.
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
