This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Particle in a One-Dimension Box – Set 2”.
1. What is the average value of position for a particle in a one-dimensional box of length a?
a) a
b) 0
c) a/2
d) a/3
View Answer
Explanation: By the mathematical definition of average, < x > = \(\frac{2}{a} \int_0^a x(sin^2(\frac{n\pi x}{a}))\)dx; from table of integrals, the part inside the integral = \(\frac{a^2}{4}\). This gives < x > = a/2. The value makes physical sense as well, because on average, the particle would be lying in the middle of this one-dimensional box.
2. What is the standard deviation of position for a particle in a box?
a) Δx = \((\frac{a}{2\pi n})(4\frac{\pi^2n^2}{3}-2)^{1/2}\)
b) Δx = \((\frac{a}{2\pi n})\)
c) Δx = \(\frac{a}{2}\)
d) Δx = \((4\frac{\pi^2n^2}{3})^{1/2}\)
View Answer
Explanation: Δx = \(\sqrt{\lt x^2\gt – \lt x \gt^2}\) = \(\sqrt{\frac{2}{a} \int_0^a x^2(sin^2(\frac{n\pi x}{a}))dx-(\frac{2}{a} \int_0^a x(sin^2(\frac{n\pi x}{a}))dx)^2}\). Simplifying the math and integrals gives Δx = \((\frac{a}{2\pi n})(4\frac{\pi^2 n^2}{3}-2)^{1/2}\).
3. What is the average momentum for a particle in a box?
a) < px > = (a/2πn)2
b) < px > = \((\frac{a}{2\pi n})^2 (\frac{n^2 \pi^2}{3m})\)
c) 0
d) < px > = \(\frac{2\pi n}{a}\)
View Answer
Explanation: The momentum operator is -iħ\(\frac{d}{dx}\rightarrow \int_0^a[(\frac{2}{a})^{\frac{1}{2}} sin \frac{n \pi x}{a}]\)(-iħ \(\frac{d}{dx} ((\frac{2}{a})^{\frac{1}{2}} sin \frac{n \pi x}{a})\)dx = -iħ \(\frac{2\pi n}{a} \int_0^a sin \frac{n \pi x}{a} cos \frac{n \pi x}{a}\)dx. Since cosine is an even function, and sine is an odd function, their product is an odd function, and the subsequent integral over all space in that particle in a box will be 0; hence causing average momentum to be 0. This makes sense because a particle cannot continue to travel in one direction.
4. What is the value of < px >2 for a particle in a box?
a) \(\frac{n^2 π^2 \hbar^2}{a^2}\)
b) \(\frac{n π \hbar}{a}\)
c) \(\frac{n^2 \hbar^2}{a^2}\)
d) 0
View Answer
Explanation: The momentum operator is -iħ\(\frac{d}{dx}\rightarrow \lt p_x^2 \gt = \int_0^a[(\frac{2}{a})^{\frac{1}{2}}\) sin \(\frac{n \pi x}{a}] \int_0^a[(\frac{2}{a})^{\frac{1}{2}}\) sin \(\frac{n \pi x}{a}]\)(-iħ\(\frac{d}{dx})^2 ((\frac{2}{a})^{\frac{1}{2}}\) sin \(\frac{n \pi x}{a})\)dx – → The double derivative gives back the sin term, which after simplification yields \(\lt p_x^2 \gt = \frac{n^2 π^2 \hbar^2}{a^2}\).
5. What is the standard deviation in momentum for a particle in a one-dimension box?
a) \(\frac{n^2 π^2 \hbar^2}{a^2}\)
b) \(\frac{n π \hbar}{a}\)
c) 0
d) \(\frac{n^2 \hbar^2}{a^2}\)
View Answer
Explanation: Δpx = \(\sqrt{(\lt p_x^2 \gt – \lt p_x \gt^2)^\frac{1}{2}} = \sqrt{\frac{n^2 π^2 \hbar^2}{a^2}-0} = \frac{n \pi h}{a}\)
6. What is the ground state energy (in Joules) for an electron that is confined to a potential well of width 0.4nm?
a) 1.506 × 10-18 J
b) 3.765 × 10-19 J
c) 1.506 × 1018 J
d) 7.534 × 10-20 J
View Answer
Explanation: Plugging into the energy equation En = \(\frac{h^2 n^2}{8ma^2}\) for n = 1 gives En = \(\frac{(6.626×10^{-34} Js)^2(1)^2}{8×(9.109×10^{-31} kg)×(0.2×10^{-9} m)^2}\) = 1.506×10-18 J
7. For a particle in aa box with wavefunction φ(x) = B sin \(\frac{nπx}{a}\), what is the constant B?
a) \((\frac{2}{a})^\frac{1}{2}\)
b) \((\frac{1}{a})\)
c) 1
d) (2πa)1/2
View Answer
Explanation: For a normalized wavefunction, \(\int_0^a\) φ*(x)φ(x)dx = |B|2 \(\int_0^a\)(sin2\((\frac{n\pi x}{a}))\)dx — → Using double angle formula this is broken up and integrated to give |B|2 \(\frac{a}{2}\) = 1—→ B = \((\frac{2}{a})^{\frac{1}{2}} \)
8. An electron moves freely with kinetic energy E = 100 eV in region 1, where the potential energy is 0. It suddenly encounters an increasing potential until V = 75 eV in region 2, which slows it down. In region 3, it continues to move with the same total energy and constant potential of V = 75 eV. What is the wavefunction form in region 1?
a) φ(x) = Aeik1x ; where k1 = \(\frac{\sqrt{2mE}}{\hbar}\)
b) φ(x) = Aeik1x + Be-ik1x; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\)
c) φ(x) = Be-ik1x; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\)
d) φ(x) = Aeik1x + Be-ik1x; where k1 = \(\frac{\sqrt{2mE}}{\hbar}\)
View Answer
Explanation: Since there is no potential barrier in region 1, the wavefunction assumes the normal form of φ(x) = Aeik1x + Be-ik1x; where k1 = \(\frac{\sqrt{2mE}}{\hbar}\). This is the regular solution obtained to the differential equation for a particle in a one-dimensional box.
9. An electron moves freely with kinetic energy E = 100 eV in region 1, where the potential energy is 0. It suddenly encounters an increasing potential until V = 75 eV in region 2, which slows it down. In region 3, it continues to move with the same total energy and constant potential of V = 75 eV. What is the wavefunction form in region 2?
a) φ(x) = Aeik1x ; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\)
b) φ(x) = Aeik1x + Be-ik1x; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\)
c) φ(x) = Be-ik1x; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\)
d) φ(x) = Aeik1x + Be-ik1x; where k1 = \(\frac{\sqrt{2mE}}{\hbar}\)
View Answer
Explanation: Since there is a constant potential barrier, the wavefunction at any point in time for this system will be given by φ(x) = Aeik1x ; where k1 = \(\frac{\sqrt{2m(E-V)}}{\hbar}\). This corresponds to the solution obtained for a particle in a box moving in a potential step well lower than the kinetic energy of the particle.
10. An electron moves freely with kinetic energy E = 100 eV in region 1, where the potential energy is 0. It suddenly encounters an increasing potential until V = 75 eV in region 2, which slows it down. In region 3, it continues to move with the same total energy and constant potential of V = 75 eV. What is the ratio of De Broglie wavelengths in region 2 VS region 1?
a) 1
b) 2
c) 1.5
d) ∞
View Answer
Explanation: De Broglie wavelength λDB = \(\frac{h}{p}\), p = ħk; Region 1: λ1 = \(\frac{h}{\sqrt{2mE}}\);
Region 2: λ2 = \(\frac{h}{\sqrt{2m(E-V)}}\); \(\frac{\lambda_2}{\lambda_1}=\frac{\sqrt{E}}{\sqrt{E-V}}=\frac{\sqrt{100}}{\sqrt{100-75}}=\frac{10}{5}\) = 2
11. A particle in a one-dimensional box is showed in the image below. The coordinates for the same are shifted from the original treatment of the particle in a box. What are the boundary conditions for this wavefunction?
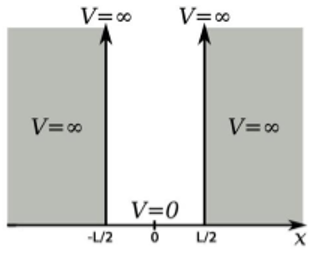
a) φ\((\frac{L}{2})\) = φ\((-\frac{L}{2})\) = ∞
b) φ\((\frac{L}{2})\) = φ\((-\frac{L}{2})\) = -∞
c) φ\((\frac{L}{2})\) = φ\((-\frac{L}{2})\) = 0
d) φ\((\frac{L}{2})\) = φ\((-\frac{L}{2})\) = 1
View Answer
Explanation: The boundary conditions remain same regardless of changes in coordinates. Since the wavefunction is non-existent outside the box, it must be 0 on the boundary as well for it to be continuous.
12. A particle in a one-dimensional box is showed in the image below. The coordinates for the same are shifted from the original treatment of the particle in a box. What is the time independent Schrodinger equation for |x|≤L/2?

a) \(\frac{-\hbar^2}{2m} \frac{d^2 \varphi}{dx^2}\) = Eφ
b) \(\frac{-\hbar^2}{2m} \frac{d^2 \varphi}{dx^2}\) + V(x)φ(x) = Eφ
c) \(\frac{-\hbar^2}{2m} \frac{d^2 \varphi}{dx^2}\) + V(x)\(\frac{d\varphi}{dx}\) = Eφ
d) \(\frac{-\hbar^2}{2m} \frac{d^2 \varphi}{dx^2}\) = E \(\frac{d\varphi}{dx}\)
View Answer
Explanation: From the regular Schrodinger equation, the potential term is equal to 0 which reduces the left-hand side of the equation to one term. This makes it an ordinary differential equation with the total energy term on the right-hand side. This is no change as compared to the equation for a particle in a box which is not shifted.
13. A particle in a one-dimensional box is showed in the image below. The coordinates for the same are shifted from the original treatment of the particle in a box. Using the boundary conditions, what is a value of k?

a) k = \(\frac{2\pi n}{L}\)
b) k = πnL
c) k = \(\frac{(2n+1)\pi}{L}\)
d) k = 2πnL
View Answer
Explanation: Solution to the differential equation is φ(x) = A sin kx + B cos kx. At the boundary conditions of x = L/2 and x = -L/2, the wavefunction is 0. This gives A sin \(\frac{kL}{2}\) + B cos \(\frac{kL}{2}\) = 0 and –A sin \(\frac{kL}{2}\) + B cos \(\frac{kL}{2}\) = 0. Summing these two up gives 2B cos\(\frac{kL}{2}\) = 0—→\(\frac{kL}{2}\) = \(\frac{\pi}{2}\) + πn — → k = \(\frac{(2n+1)\pi}{L}\) .
14. The eigenfunctions for a particle in a 1-D box are φ(x) = \(\sqrt{\frac{2}{L}} cos \frac{\pi nx}{L}\). What is the probability that a particle in the ground state will be found between x = -0.01L and x = 0.01L?
a) 0
b) 1
c) 0.02
d) 0.04
View Answer
Explanation: Probability is given by P = |φ(x)|2 dx = \(\frac{2}{L}\int_{-0.01L}^{0.01L}\) (cos2 \(\frac{\pi nx}{L})\)dx. The part inside the integral can be approximated as the area of a rectangle as the bounds are very small in comparison to the size of the box. Hence, P = \(\frac{2}{L}\) × 0.02L = 0.04.
15. The eigenfunctions for a particle in a 1-D box are φ(x) = \(\sqrt{\frac{2}{L}}\) cos \(\frac{\pi nx}{L}\). What is the expectation value of linear momentum p for a particle in its ground state?
a) 0
b) 1
c) 0.5
d) 0.33
View Answer
Explanation: < p > = \(\int_{-\infty}^\infty\) φ1(x) (-iħ \(\frac{\partial \varphi_1(x)}{\partial x})\)dx = iħ \(\int_{-\infty}^\infty\) cos \(\frac{\pi x}{L}\) sin \(\frac{\pi x}{L}\)dx = 0. Since cosine is an even function and sine is an odd function, the overall right-hand side function inside the integral is odd. This is equal to 0 as the integral of an odd function over all space is 0 (positive and negative parts cancel out).
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
