This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Heisenberg Uncertainty Principle”.
1. What is the main difference between the determination of position and momentum of a particle in classical and quantum mechanics?
a) The position and momentum of a particle can be known exactly in quantum mechanics, whereas they are known with uncertainty in classical mechanics
b) The position and momentum of a particle can be known exactly in classical mechanics, whereas they are known with uncertainty in quantum mechanics
c) Neither field limits the accuracy or precision of position and momentum of a particle
d) Position and momentum only exist in classical mechanics
View Answer
Explanation: Classical mechanics has no uncertainty bounds for measuring position and momentum, whereas this uncertainty arises in quantum mechanics. Position and momentum are variables existing in classical as well as quantum mechanics. Quantum mechanics specifically states this uncertainty for the product of specific variable pairs.
2. Which other variable pairs (other than momentum and position) are important observables in Heisenberg’s uncertainty principle?
a) Momentum and velocity
b) Time and position
c) Energy and momentum
d) Energy and time
View Answer
Explanation: Substituting E = hv in Heisenberg’s uncertainty principle for position and momentum gives an expression in terms of energy and time as another variable pair that appears in this uncertainty principle. Momentum and velocity, time and position, and energy and momentum are not complementary pairs in this regard.
3. Heisenberg’s principle involving position and momentum is given by: ΔpxΔx > \(\frac{h}{4\pi}\), where ‘h’ is Plank’s constant What is the minimum uncertainty in momentum of an electron if uncertainty in its position is 50 pm (picometers)?
a) 5.27 × 10-25 kgms-1
b) 5.27 × 10-25 gms-1
c) 1.054 × 10-25 kgms-1
d) 1.054 × 10-25 gms-1
View Answer
Explanation: Re-arranging the given expression for Heisenberg’s uncertainty principle, Δpx > \(\frac{h}{4\pi\Delta x}\), giving Δpx > \(\frac{6.626×10^{-34}Js}{4×\pi×50×10^{-12}m}\) = 1.054 × 10-24 kgms-1.
4. What is the minimum uncertainty in velocity of an electron if uncertainty in its position is 50 pm (picometers)?
a) 1.16 × 106 ms-1
b) 2.32 × 105 ms-1
c) 5.8 × 105 ms-1
d) 1.16 × 105 ms-1
View Answer
Explanation: Re-arranging the expression for Heisenberg’s uncertainty principle, Δpx > \(\frac{h}{4\pi\Delta x}\), giving Δpx > \(\frac{6.626×10^{-34}Js}{4×\pi×50×10^{-12}m}\) = 1.054 × 10-24 kgms-1. Δvx = \(\frac{\Delta p_x}{m}\), where ‘m’ is mass of an electron, which is known. Δvx = \(\frac{\Delta p_x}{m}\) = \(\frac{1.054×10^{-24}kgms^{-1}}{9.1094×10^{-31}kg}\) = 1.16 × 106ms-1
5. The image below is that of a superposition of waves (Made using sin function generator on fx-CG19 calculator). Assuming the horizontal to be the x-axis, hence position, what can be said about the particle’s uncertainty in position?
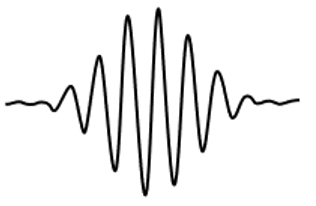
a) The waves are weakly localized, hence uncertainty in position is small
b) The waves are strongly localized, hence uncertainty in position is large
c) The waves are weakly localized, hence uncertainty in position is large
d) The waves are strongly localized, hence uncertainty in position is small
View Answer
Explanation: Since there are multiple waves in this given superposition state, it is weakly localized. A single wave would otherwise imply strong localization. Uncertainty in position is large because the waves are highly scattered. A small uncertainty would result from single, less scattered waves
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
