This set of Physical Chemistry Multiple Choice Questions & Answers (MCQs) focuses on “Quantum Mechanical Harmonic Oscillator”.
1. What is the expression for reduced mass, μ for two particles in a system of mass m1 and m2?
a) μ = m1m2
b) μ = \(\frac{m1×m2}{m1+m2}\)
c) μ = m1+m2
d) μ = \(\frac{m1+m2}{m1×m2}\)
View Answer
Explanation: Reduced mass is a weighted equivalent mass of two or more bodies in a system. It is not the same as center of mass or center of gravity as it does not specify the point in which mass is concentrated. Reduced mass is defined in this way to avoid ambiguity and simplify problems on harmonic motion.
2. What is the one-dimensional classical Hamiltonian for a body in harmonic motion with frequency ω, reduced mass μ, displacement x. and momentum p?
a) H = \(\frac{p_x^2}{2\mu} + \frac{1}{2}\) ω2 μx2
b) H = \(\frac{p_x^2}{2\mu} + \) ω2 μx2
c) H = \(\frac{1}{2}\) ω2 μx2
d) H = \(\frac{-\hbar^2}{2\mu} \frac{d^2}{dx^2} + \frac{1}{2}\) ω2 μx2
View Answer
Explanation: Hamiltonian consists of potential and kinetic energy of a body. Reduced mass is treated as the equivalent of mass in this case. The kinetic energy written in terms of momentum is T = \(\frac{p_x^2}{2\mu}\) and potential energy is V = \(\frac{1}{2}\)kx2; ω = \(\sqrt{\frac{k}{\mu}}\) —→ k = μω2 —→ V = \(\frac{1}{2}\) μω2 x2. Adding these two gives the classical Hamiltonian for a body in harmonic motion.
3. What is the one-dimensional quantum mechanical Hamiltonian for a body in harmonic motion with frequency ω, reduced mass μ, and position operator x?
a) H = \(\frac{p_x^2}{2\mu} + \frac{1}{2}\) ω2 μx2
b) H = \(\frac{p_x^2}{2\mu} + \) ω2 μx2
c) H = \(\frac{1}{2}\) ω2 μx2
d) H = \(\frac{-\hbar^2}{2\mu} \frac{d^2}{dx^2} + \frac{1}{2}\) ω2 μx2
View Answer
Explanation: Hamiltonian consists of potential and kinetic energy of a body. Reduced mass is treated as the equivalent of mass in this case. The kinetic energy written in terms of momentum (operator, which is p = -iħ\(\frac{\partial}{\partial x}\)) is T = \(\frac{-\hbar^2}{2\mu} \frac{d^2}{dx^2}\) and potential energy is V = \(\frac{1}{2}\)kx2; ω = \(\sqrt{\frac{k}{\mu}}\) —→ k = μω2 —→ V = \(\frac{1}{2}\) μω2 x2. Adding these two gives the quantum mechanical Hamiltonian for a body in harmonic motion.
4. What are the energy levels for a quantum mechanical harmonic oscillator in terms of h, and v = \((\frac{1}{2\pi}) (\frac{k}{\mu})^{\frac{1}{2}}\)?
a) E = hv
b) E = hv2
c) E = (n + \(\frac{1}{2}\)) hv
d) E = (n + \(\frac{1}{2}\)) v
View Answer
Explanation: Substituting the Hamiltonian H = \(\frac{-\hbar^2}{2\mu} \frac{d^2}{dx^2} + \frac{1}{2}\) ω2 μx2 into the Schrodinger equation for quantum mechanical harmonic oscillator yields energy levels of E = (n + \(\frac{1}{2}\)) hv, with n = 0,1,2… This further shows that the energy levels are discrete. They are equally spaced with a separation of hv.
5. What is the ground state energy of the quantum mechanical harmonic oscillator?
a) E0 = \(\frac{hv}{2}\)
b) E0 = 0
c) E0 = hv
d) E0 = \(\frac{v}{2}\)
View Answer
Explanation: Unlike the classical harmonic oscillator, the quantum mechanical oscillator has a non-zero ground state energy. Plugging n=0 for the energy levels E = (n + \(\frac{1}{2}\)) hv yields E0 = \(\frac{hv}{2}\). This is in accordance with the Heisenberg uncertainty principle.
6. What is the shape of the wavefunction for the ground state quantum mechanical harmonic oscillator?
a) Gaussian
b) Quadratic
c) Hermitian
d) Poisson
View Answer
Explanation: The ground state wavefunction is given by φ0 = \((\frac{\alpha}{\pi})^{1/4} e^{- \frac{\alpha x^2}{2}}\). This is like the bell-shaped Gaussian distribution which is asymptotic to the x-axis at ±∞. The wavefunctions in themselves contain Hermite polynomials, but the overall shape does not turn out to be that.
7. What is the expression for kinetic energy T in terms of raising and lowering operators? lowering operator: a^|φv > = √v|φ(v-1); raising operator: a✝|φv = \(\sqrt{v+1}\)|φv+1. x = \(\sqrt{\frac{\hbar}{2m \omega}}\)(a∧ + a∔); p = -i\(\sqrt{\frac{\hbar m \omega}{2}}\)(a∧ – a∔)
a) T = \(\frac{-\hbar \omega}{4}\)
b) T = (a∧ – a∔)2
c) T = \(\frac{-\hbar \omega}{4\pi}\)(a∧ + a∔)
d) T = \(\frac{-\hbar \omega}{4}\)(a∧ – a∔)2
View Answer
Explanation: T = \(\frac{p^2}{2m}\) —→ plugging the operator expressions into this equation gives T = \(\frac{-\hbar \omega}{4}\)(a∧ – a∔)2
8. What is the reduced mass μHF of an HF molecule in atomic mass units (amu)? (atomic masses: H = 1 amu, F = 19 amu)
a) 0.5
b) 1.9
c) 0.95
d) 1.75
View Answer
Explanation: μHF = \(\frac{m_H m_F}{m_H+m_F} = \frac{19×1}{19+1} = \frac{19}{20}\) = 0.95 amu
9. What is the reduced mass μDF of a DF molecule in atomic mass units (amu)? (atomic masses: D = 2 amu, F = 19 amu)
a) 1.81
b) 0.95
c) 1
d) 1.25
View Answer
Explanation: μDF = \(\frac{m_D m_F}{m_D+m_F} = \frac{19×2}{19+2} = \frac{38}{21}\) ≈ 1.81 amu
10. Vibrations of HF are described by the harmonic oscillator model. What happens to the spacing between adjacent vibration levels when hydrogen is replaced by deuterium, i.e. \(\frac{\Delta E_{DF}^{vib}}{\Delta E_{HF}^{vib}}\) = ? (atomic masses: D = 2 amu, F = 19 amu)
a) 1.353
b) 0.707
c) 1.579
d) 1
View Answer
Explanation: \(\frac{\Delta E_{DF}^{vib}}{\Delta E_{HF}^{vib}}\) = \(\sqrt{\frac{\mu_{HF}}{\mu_{DF}}} = \sqrt{\frac{19/20}{38/21}} = \sqrt{\frac{21}{40}}\) ≈ 0.707
11. The diagram below is that of a semi-harmonic oscillator with potential as shown in the diagram. What are the boundary conditions for this wavefunction?
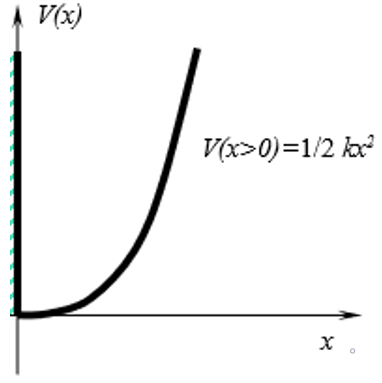
a) φ(0) = 0
b) φ(0) = ∞
c) φ(0) = -∞
d) φ(0) = 0
View Answer
Explanation: Since the wavefunction begins from x = 0, and the potential for negative values of x is infinite, the wavefunction must be zero at this point. The wavefunction can only exist if this boundary condition is satisfied.
12. The diagram below is that of a semi-harmonic oscillator with potential as shown in the diagram. The energy levels of a full harmonic oscillator are given by Ev = ħω(v + \(\frac{1}{2})\). For what values of v does the wavefunction satisfy the boundary condition φ(0) = 0?

a) For all values of v
b) For all odd number values of v
c) For all even number values of v
d) For no values of v, i.e. the wavefunction cannot satisfy quantum mechanical conditions
View Answer
Explanation: φ(0) = 0 applies only for odd values of v. This is because all odd values of energy levels have a wavefunction form that has an x dependence in them, for ex: φ1 = \((\frac{4\alpha^3}{\pi})^{1/4}\) xexp \((\frac{-\alpha x^2}{2})\) and so on. This makes the right-hand side zero and hence satisfy the boundary conditions. Thus, v = 2k + 1, k = 0, 1, 2…
13. The diagram below is that of a semi-harmonic oscillator with potential as shown in the diagram. The energy levels of a full harmonic oscillator are given by Ev = ħω(v + \(\frac{1}{2})\). What are the energy levels for a semi-harmonic oscillator for all whole number values of k?

a) E = ħω(k + \(\frac{1}{2}\))
b) E = ħωk
c) E = ħω(k + \(\frac{3}{2}\))
d) E = ħω(2k + \(\frac{3}{2}\))
View Answer
Explanation: φ(0) = 0 applies only for odd values of v in the original energy expression of Ev = ħω(v + \(\frac{1}{2}\)). This is because all odd values of energy levels have a wavefunction form that has an x dependence in them, for ex: φ1 = \((\frac{4\alpha^3}{\pi})^{1/4}\) xexp \((\frac{-\alpha x^2}{2})\) and so on. This makes the right-hand side zero and hence satisfy the boundary conditions. Hence, for all whole number values of k, E = ħω(2k + \(\frac{3}{2}\)) satisfies the boundary conditions for this semi-harmonic oscillator.
14. The diagram below is that of a semi-harmonic oscillator with potential as shown in the diagram. The energy levels of a full harmonic oscillator are given by Ev = ħω(v + \(\frac{1}{2})\). What is the zero-point energy for a semi-harmonic oscillator?
a) E0 = \(\frac{3}{2}\) ħω
b) E0 = \(\frac{1}{2}\) ħω
c) E0 = ħω
d) E0 = 2ħω

View Answer
Explanation: φ(0) = 0 applies only for odd values of v in the original energy expression of Ev = ħω(v + \(\frac{1}{2}\)). This is because all odd values of energy levels have a wavefunction form that has an x dependence in them, for ex: φ1 = \((\frac{4\alpha^3}{\pi})^{1/4}\) xexp \((\frac{-\alpha x^2}{2})\) and so on. This makes the right-hand side zero and hence satisfy the boundary conditions. Hence, for all whole number values of k, E = ħω(2k + \(\frac{3}{2}\)) satisfies the boundary conditions for this semi-harmonic oscillator. Plugging in k = 0 (ground state energy) for this equation gives E0 = \(\frac{3}{2}\) ħω.
15. What is the type of polynomial function that is a part of the harmonic oscillator wavefunction?
a) Binominal
b) Hermite
c) Monomial
d) Trinomial
View Answer
Explanation: The general wavefunction form of harmonic oscillators is given by φv(x) = NvHv(α1/2x)\(e^{\frac{-\alpha x^2}{2}}\), where Nv is the Hermite polynomial given by Nv = \(\frac{1}{(2^v v!)^{\frac{1}{2}}} (\frac{\alpha}{\pi})^{1/4}\)
Sanfoundry Global Education & Learning Series – Physical Chemistry.
To practice all areas of Physical Chemistry, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
