This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “Frequency Analysis of Continuous Time Signals”.
1. The Fourier series representation of any signal x(t) is defined as ___________
a) \(\sum_{k=-\infty}^{\infty}c_k e^{j2πkF_0 t}\)
b) \(\sum_{k=0}^{\infty}c_k e^{j2πkF_0 t}\)
c) \(\sum_{k=-\infty}^{\infty}c_k e^{-j2πkF_0 t}\)
d) \(\sum_{k=-\infty}^{\infty}c_{-k} e^{j2πkF_0 t}\)
View Answer
Explanation: If the given signal is x(t) and F0 is the reciprocal of the time period of the signal and ck is the Fourier coefficient then the Fourier series representation of x(t) is given as \(\sum_{k=-\infty}^{\infty}c_k e^{j2πkF_0 t}\).
2. Which of the following is the equation for the Fourier series coefficient?
a) \(\frac{1}{T_p} \int_0^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
b) \(\frac{1}{T_p} \int_{t_0}^∞ x(t)e^{-j2πkF_0 t} dt\)
c) \(\frac{1}{T_p} \int_{t_0}^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
d) \(\frac{1}{T_p} \int_{t_0}^{t_0+T_p} x(t)e^{j2πkF_0 t} dt\)
View Answer
Explanation: When we apply integration to the definition of Fourier series representation, we get
ckTp=\(\int_{t_0}^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
=>ck=\(\frac{1}{T_p} \int_{t_0}^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
3. Which of the following is a Dirichlet condition with respect to the signal x(t)?
a) x(t) has a finite number of discontinuities in any period
b) x(t) has finite number of maxima and minima during any period
c) x(t) is absolutely integrable in any period
d) all of the mentioned
View Answer
Explanation: For any signal x(t) to be represented as Fourier series, it should satisfy the Dirichlet conditions which are x(t) has a finite number of discontinuities in any period, x(t) has finite number of maxima and minima during any period and x(t) is absolutely integrable in any period.
4. The equation x(t)=\(\sum_{k=-\infty}^{\infty}c_k e^{j2πkF_0 t}\) is known as analysis equation.
a) True
b) False
View Answer
Explanation: Since we are synthesizing the Fourier series of the signal x(t), we call it as synthesis equation, where as the equation giving the definition of Fourier series coefficients is known as analysis equation.
5. Which of the following is the Fourier series representation of the signal x(t)?
a) \(c_0+2\sum_{k=1}^{\infty}|c_k|sin(2πkF_0 t+θ_k)\)
b) \(c_0+2\sum_{k=1}^{\infty}|c_k|cos(2πkF_0 t+θ_k)\)
c) \(c_0+2\sum_{k=1}^{\infty}|c_k|tan(2πkF_0 t+θ_k)\)
d) None of the mentioned
View Answer
Explanation: In general, Fourier coefficients ck are complex valued. Moreover, it is easily shown that if the periodic signal is real, ck and c-k are complex conjugates. As a result
ck=|ck|ejθkand ck=|ck|e-jθk
Consequently, we obtain the Fourier series as x(t)=\(c_0+2\sum_{k=1}^{\infty}|c_k|cos(2πkF_0 t+θ_k)\)
6. The equation x(t)=\(a_0+\sum_{k=1}^∞(a_k cos2πkF_0 t – b_k sin2πkF_0 t)\) is the representation of Fourier series.
a) True
b) False
View Answer
Explanation: cos(2πkF0 t+θk) = cos2πkF0 t.cosθk-sin2πkF0 t.sinθk
θk is a constant for a given signal.
So, the other form of Fourier series representation of the signal x(t) is
\(a_0+\sum_{k=1}^∞(a_k cos2πkF_0 t – b_k sin2πkF_0 t)\).
7. The equation of average power of a periodic signal x(t) is given as ___________
a) \(\sum_{k=0}^{\infty}|c_k|^2\)
b) \(\sum_{k=-\infty}^{\infty}|c_k|\)
c) \(\sum_{k=-\infty}^0|c_k|^2\)
d) \(\sum_{k=-\infty}^{\infty}|c_k|^2\)
View Answer
Explanation: The average power of a periodic signal x(t) is given as
The average power of a periodic signal x(t) is given as \(\frac{1}{T_p} \int_{t_0}^{t_0+T_p}|x(t)|^2 dt\)
=\(\frac{1}{T_p} \int_{t_0}^{t_0+T_p}x(t).x^* (t) dt\)
=\(\frac{1}{T_p} \int_{t_0}^{t_0+T_p}x(t).\sum_{k=-\infty}^{\infty} c_k * e^{-j2πkF_0 t} dt\)
By interchanging the positions of integral and summation and by applying the integration, we get
=\(\sum_{k=-\infty}^{\infty}|c_k |^2\)
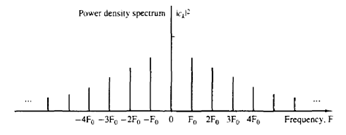
8. What is the spectrum that is obtained when we plot |ck |2 as a function of frequencies kF0, k=0,±1,±2..?
a) Average power spectrum
b) Energy spectrum
c) Power density spectrum
d) None of the mentioned
View Answer
Explanation: When we plot a graph of |ck|2 as a function of frequencies kF0, k=0,±1,±2… the following spectrum is obtained which is known as Power density spectrum.
9. What is the spectrum that is obtained when we plot |ck| as a function of frequency?
a) Magnitude voltage spectrum
b) Phase spectrum
c) Power spectrum
d) None of the mentioned
View Answer
Explanation: We know that, Fourier series coefficients are complex valued, so we can represent ck in the following way.
ck=|ck|ejθk
When we plot |ck| as a function of frequency, the spectrum thus obtained is known as Magnitude voltage spectrum.
10. What is the equation of the Fourier series coefficient ck of an non-periodic signal?
a) \(\frac{1}{T_p} \int_0^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
b) \(\frac{1}{T_p} \int_{-\infty}^∞ x(t)e^{-j2πkF_0 t} dt\)
c) \(\frac{1}{T_p} \int_{t_0}^{t_0+T_p} x(t)e^{-j2πkF_0 t} dt\)
d) \(\frac{1}{T_p} \int_{t_0}^{t_0+T_p} x(t)e^{j2πkF_0 t} dt\)
View Answer
Explanation: We know that, for an periodic signal, the Fourier series coefficient is
ck=\(\frac{1}{T_p} \int_{-T_p/2}^{T_p/2} x(t)e^{-j2πkF_0 t} dt\)
If we consider a signal x(t) as non-periodic, it is true that x(t)=0 for |t|>Tp/2. Consequently, the limits on the integral in the above equation can be replaced by -∞ to ∞. Hence,
ck=\(\frac{1}{T_p} \int_{-\infty}^∞ x(t)e^{-j2πkF_0 t} dt\)
11. Which of the following relation is correct between Fourier transform X(F) and Fourier series coefficient ck?
a) ck=X(F0/k)
b) ck= 1/TP (X(F0/k))
c) ck= 1/TP(X(kF0))
d) none of the mentioned
View Answer
Explanation: Let us consider a signal x(t) whose Fourier transform X(F) is given as
X(F)=\(\int_{-∞}^∞ x(t)e^{-j2πF_0 t}dt\)
and the Fourier series coefficient is given as
ck=\(\frac{1}{T_p} \int_{-∞}^∞ x(t)e^{-j2πkF_0 t}dt\)
By comparing the above two equations, we get
ck=\(\frac{1}{T_p} X(kF_0)\)
12. According to Parseval’s Theorem for non-periodic signal, \(\int_{-∞}^∞|x(t)|^2 dt\).
a) \(\int_{-∞}^∞|X(F)|^2 dt \)
b) \(\int_{-∞}^∞|X^* (F)|^2 dt \)
c) \(\int_{-∞}^∞ X(F).X^*(F) dt \)
d) All of the mentioned
View Answer
Explanation: Let x(t) be any finite energy signal with Fourier transform X(F). Its energy is
Ex=\(\int_{-∞}^∞|x(t)|^2 dt\)
which in turn, can be expressed in terms of X(F) as follows
Ex=\(\int_{-∞}^∞ x^* (t).x(t)\) dt
=\(\int_{-∞}^∞ x(t) dt[\int_{-∞}^∞X^* (F)e^{-j2πF_0 t} dt]\)
=\(\int_{-∞}^∞ X^* (F) dt[\int_{-∞}^∞ x(t)e^{-j2πF_0 t} dt] \) \(=\int_{-∞}^∞ |X(F)|^2 dt = \int_{-∞}^∞|X^* (F)|^2 dt = \int_{-∞}^∞X(F).X^* (F) dt\)
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
