This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “Rational Z Transform”.
1. What are the values of z for which the value of X(z)=0?
a) Poles
b) Zeros
c) Solutions
d) None of the mentioned
View Answer
Explanation: For a rational z-transform X(z) to be zero, the numerator of X(z) is zero and the solutions of the numerator are called as ‘zeros’ of X(z).
2. What are the values of z for which the value of X(z)=∞?
a) Poles
b) Zeros
c) Solutions
d) None of the mentioned
View Answer
Explanation: For a rational z-transform X(z) to be infinity, the denominator of X(z) is zero and the solutions of the denominator are called as ‘poles’ of X(z).
3. If X(z) has M finite zeros and N finite poles, then which of the following condition is true?
a) |N-M| poles at origin(if N>M)
b) |N+M| zeros at origin(if N>M)
c) |N+M| poles at origin(if N>M)
d) |N-M| zeros at origin(if N>M)
View Answer
Explanation: If X(z) has M finite zeros and N finite poles, then X(z) can be rewritten as X(z)=z -M+N.X'(z).
So, if N>M then z has a positive power. So, it has |N-M| zeros at origin.
4. If X(z) has M finite zeros and N finite poles, then which of the following condition is true?
a) |N-M| poles at origin(if N < M)
b) |N+M| zeros at origin(if N < M)
c) |N+M| poles at origin(if N < M)
d) |N-M| zeros at origin(if N < M)
View Answer
Explanation: If X(z) has M finite zeros and N finite poles, then X(z) can be rewritten as X(z)=z-M+N.X'(z).
So, if N < M then z has a negative power. So, it has |N-M| poles at origin.
5. Which of the following signals have a pole-zero plot as shown below?
a) a.u(n)
b) u(an)
c) anu(n)
d) none of the mentioned
View Answer
Explanation: From the given pole-zero plot, the z-transform of the signal has one zero at z=0 and one pole at z=a.
So, we obtain X(z)=z/(z-a)
By applying inverse z-transform for X(z), we get
x(n)= anu(n).
6. Which of the following signals have a pole-zero plot as shown below?(Let M=8 in the figure)
a)
x(n)=an, 0≤n≤8
=0, elsewhere
b)
x(n)=an, 0≤n≤7
=0, elsewhere
c)
x(n)=a-n, 0≤n≤8
=0, elsewhere
d)
x(n)=a-n, 0≤n≤7
=0, elsewhere
View AnswerExplanation: From the figure given, the z-transform of the signal has 8 zeros on circle of radius ‘a’ and 7 poles at origin.
So, X(z) is of the form X(z)=\(\frac{(z-z_1) (z-z_2)……(z-z_8)}{z^7}\)
By applying inverse z-transform, we get x(n)=an, 0≤n≤7
=0, elsewhere.
7. The z-transform X(z) of the signal x(n)=anu(n) has:
a) One pole at z=0 and one zero at z=a
b) One pole at z=0 and one zero at z=0
c) One pole at z=a and one zero at z=a
d) One pole at z=a and one zero at z=0
View Answer
Explanation: The z-transform of the given signal is X(z)=z/(z-a)
So, it has one pole at z=a and one zero at z=0.
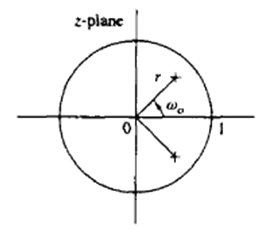
8. What is the nature of the signal whose pole-zero plot is as shown?
a) Rising signal
b) Constant signal
c) Decaying signal
d) None of the mentioned
View Answer
Explanation: From the pole-zero plot, it is shown that r < 1, so the signal is a decaying signal.
9. What are the values of z for which the value of X(z)=0?
a) Poles
b) Zeros
c) Solutions
d) None of the mentioned
View Answer
Explanation: For a rational z-transform X(z) to be zero, the numerator of X(z) is zero and the solutions of the numerator are called as ‘zeros’ of X(z).
10. If Y(z) is the z-transform of the output function, X(z) is the z-transform of the input function and H(z) is the z-transform of system function of the LTI system, then H(z)=?
a) \(\frac{Y(z)}{X(z)}\)
b) \(\frac{X(z)}{Y(z)}\)
c) Y(z).X(z)
d) None of the mentioned
View Answer
Explanation: We know that for an LTI system, y(n)=h(n)*x(n)
On applying z-transform on both sides we get, Y(z)=H(z).X(z)=>H(z)=\(\frac{Y(z)}{X(z)}\).
11. What is the system function of the system described by the difference equation y(n)=0.5y(n-1)+2x(n)?
a) \(\frac{2}{1+0.5z^{-1}}\)
b) \(\frac{0.5}{1+2z^{-1}}\)
c) \(\frac{0.5}{1-2z^{-1}}\)
d) \(\frac{2}{1-0.5z^{-1}}\)
View Answer
Explanation: Given difference equation of the system is y(n)=0.5y(n-1)+2x(n)
On applying z-transform on both sides we get, Y(z)=0.5z-1Y(z)+2X(z)
=>\(\frac{Y(z)}{X(z)}=\frac{2}{1-0.5z^{-1}}\)=H(z).
12. What is the unit sample response of the system described by the difference equation y(n)=0.5y(n-1)+2x(n)?
a) 0.5(2)nu(n)
b) 2(0.5)nu(n)
c) 0.5(2)nu(-n)
d) 2(0.5)nu(-n)
View Answer
Explanation: By applying the z-transform on both sides of the difference equation given in the question we obtain,
\(\frac{Y(z)}{X(z)}=\frac{2}{1-0.5z^{-1}}\)=H(z)
By applying the inverse z-transform we get h(n)=2(0.5)nu(n).
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
