This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “Linear Filtering Approach to Computation of DFT”.
1. If the desired number of values of the DFT is less than log2N, a direct computation of the desired values is more efficient than FFT algorithm.
a) True
b) False
View Answer
Explanation: To calculate a N point DFT using FFT algorithm, we need to perform (N/2) log2N multiplications and N log2N additions. But in some cases where desired number of values of the DFT is less than log2N such a huge complexity is not required. So, direct computation of the desired values is more efficient than FFT algorithm.
2. What is the transform that is suitable for evaluating the z-transform of a set of data on a variety of contours in the z-plane?
a) Goertzel Algorithm
b) Fast Fourier transform
c) Chirp-z transform
d) None of the mentioned
View Answer
Explanation: Chirp-z transform algorithm is suitable for evaluating the z-transform of a set of data on a variety of contours in the z-plane. This algorithm is also formulated as a linear filtering of a set of input data. As a consequence, the FFT algorithm can be used to compute the Chirp-z transform.
3. According to Goertzel Algorithm, if the computation of DFT is expressed as a linear filtering operation, then which of the following is true?
a) yk(n)=\(\sum_{m=0}^N x(m)W_N^{-k(n-m)}\)
b) yk(n)=\(\sum_{m=0}^{N+1} x(m)W_N^{-k(n-m)}\)
c) yk(n)=\(\sum_{m=0}^{N-1} x(m)W_N^{-k(n+m)}\)
d) yk(n)=\(\sum_{m=0}^{N-1} x(m)W_N^{-k(n-m)}\)
View Answer
Explanation: Since WN-kN = 1, multiply the DFT by this factor. Thus
X(k)=WN-kN\(\sum_{m=0}^{N-1} x(m)W_N^{-km}=\sum_{m=0}^{N-1} x(m)W_N^{-k(N-m)}\)
The above equation is in the form of a convolution. Indeed, we can define a sequence yk(n) as
yk(n)=\(\sum_{m=0}^{N-1} x(m)W_N^{-k(n-m)}\)
4. If yk(n) is the convolution of the finite duration input sequence x(n) of length N, then what is the impulse response of the filter?
a) WN-kn
b) WN-kn u(n)
c) WNkn u(n)
d) None of the mentioned
View Answer
Explanation: We know that yk(n)=\(\sum_{m=0}^{N-1} x(m)W_N^{-k(n-m)}\)
The above equation is of the form yk(n)=x(n)*hk(n)
Thus we obtain, hk(n)= WN-kn u(n).
5. What is the system function of the filter with impulse response hk(n)?
a) \(\frac{1}{1-W_N^{-k} z^{-1}}\)
b) \(\frac{1}{1+W_N^{-k} z^{-1}}\)
c) \(\frac{1}{1-W_N^k z^{-1}}\)
d) \(\frac{1}{1+W_N^k z^{-1}}\)
View Answer
Explanation: We know that hk(n)= WN-kn u(n)
On applying z-transform on both sides, we get
Hk(z)=\(\frac{1}{1-W_N^{-k} z^{-1}}\)
6. What is the expression to compute yk(n) recursively?
a) yk(n)=WN-kyk(n+1)+x(n)
b) yk(n)=WN-kyk(n-1)+x(n)
c) yk(n)=WNkyk(n+1)+x(n)
d) None of the mentioned
View Answer
Explanation: We know that hk(n)=WN-kn u(n)=yk(n)/x(n)
=> yk(n)=WN-kyk(n-1)+x(n).
7. What is the equation to compute the values of the z-transform of x(n) at a set of points {zk}?
a) \(\sum_{n=0}^{N-1} x(n) z_k ^n\), k=0,1,2…L-1
b) \(\sum_{n=0}^{N-1} x(n) z_{-k}^{-n}\), k=0,1,2…L-1
c) \(\sum_{n=0}^{N-1} x(n) z_k^{-n}\), k=0,1,2…L-1
d) None of the mentioned
View Answer
Explanation: According to the Chirp-z transform algorithm, if we wish to compute the values of the z-transform of x(n) at a set of points {zk}. Then,
X(zk)=\(\sum_{n=0}^{N-1} x(n) z_k^{-n}\), k=0,1,2…L-1
8. If the contour is a circle of radius r and the zk are N equally spaced points, then what is the value of zk?
a) re-j2πkn/N
b) rejπkn/N
c) rej2πkn
d) rej2πkn/N
View Answer
Explanation: We know that, if the contour is a circle of radius r and the zk are N equally spaced points, then what is the value of zk is given by rej2πkn/N
9. How many multiplications are required to calculate X(k) by chirp-z transform if x(n) is of length N?
a) N-1
b) N
c) N+1
d) None of the mentioned
View Answer
Explanation: We know that yk(n)=WN-kyk(n-1)+x(n).Each iteration requires one multiplication and two additions. Consequently, for a real input sequence x(n), this algorithm requires N+1 real multiplications to yield not only X(k) but also, due to symmetry, the value of X(N-k).
10. If the contour on which the z-transform is evaluated is as shown below, then which of the given condition is true?
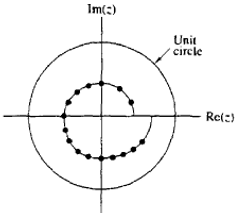
a) R0>1
b) R0<1
c) R0=1
d) None of the mentioned
View Answer
Explanation: From the definition of chirp z-transform, we know that V=R0ejθ.
If R0>1, then the contour which is used to calculate z-transform is as shown below.
11. How many complex multiplications are need to be performed to calculate chirp z-transform?(M=N+L-1)
a) log2M
b) Mlog2M
c) (M-1)log2M
d) Mlog2(M-1)
View Answer
Explanation: Since we will compute the convolution via the FFT, let us consider the circular convolution of the N point sequence g(n) with an M point section of h(n) where M>N. In such a case, we know that the first N-1 points contain aliasing and that the remaining M-N+1 points are identical to the result that would be obtained from a linear convolution of h(n) with g(n). In view of this, we should select a DFT of size M=L+N-1. Thus the total number of complex multiplications to be performed are Mlog2M.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
