This set of tough Digital Signal Processing Questions & Answers focuses on “Sampling Rate Conversion by a Rational Factor I/D”.
1. Sampling rate conversion by the rational factor I/D is accomplished by what connection of interpolator and decimator?
a) Parallel
b) Cascade
c) Convolution
d) None of the mentioned
View Answer
Explanation: A sampling rate conversion by the rational factor I/D is accomplished by cascading an interpolator with a decimator.
2. Which of the following has to be performed in sampling rate conversion by rational factor?
a) Interpolation
b) Decimation
c) Either interpolation or decimation
d) None of the mentioned
View Answer
Explanation: We emphasize that the importance of performing the interpolation first and decimation second, is to preserve the desired spectral characteristics of x(n).
3. Which of the following operation is performed by the blocks given the figure below?
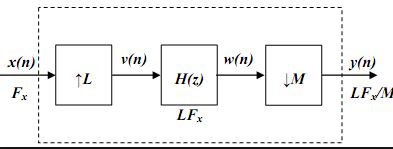
a) Sampling rate conversion by a factor I
b) Sampling rate conversion by a factor D
c) Sampling rate conversion by a factor D/I
d) Sampling rate conversion by a factor I/D
View Answer
Explanation: In the diagram given, a interpolator is in cascade with a decimator which together performs the action of sampling rate conversion by a factor I/D.
4. The Nth root of unity WN is given as _____________
a) ej2πN
b) e-j2πN
c) e-j2π/N
d) ej2π/N
View Answer
Explanation: We know that the Discrete Fourier transform of a signal x(n) is given as
X(k)=\(\sum_{n=0}^{N-1} x(n)e^{-j2πkn/N}=\sum_{n=0}^{N-1} x(n) W_N^{kn}\)
Thus we get Nth rot of unity WN= e-j2π/N
5. Which of the following is true regarding the number of computations requires to compute an N-point DFT?
a) N2 complex multiplications and N(N-1) complex additions
b) N2 complex additions and N(N-1) complex multiplications
c) N2 complex multiplications and N(N+1) complex additions
d) N2 complex additions and N(N+1) complex multiplications
View Answer
Explanation: The formula for calculating N point DFT is given as
X(k)=\(\sum_{n=0}^{N-1} x(n)e^{-j2πkn/N}\)
From the formula given at every step of computing we are performing N complex multiplications and N-1 complex additions. So, in a total to perform N-point DFT we perform N2 complex multiplications and N(N-1) complex additions.
6. Which of the following is true?
a) \(W_N^*=\frac{1}{N} W_{N^{-1}}\)
b) \(W_N-1=\frac{1}{N} W_{N^*}\)
c) \(W_N-1=W_{N^*}\)
d) None of the mentioned
View Answer
Explanation: If XN represents the N point DFT of the sequence xN in the matrix form, then we know that XN = WN.xN
By pre-multiplying both sides by WN-1, we get
xN=WN-1.XN
But we know that the inverse DFT of XN is defined as
xN=1/
Thus by comparing the above two equations we get
WN-1=1/N WN*
7. What is the DFT of the four point sequence x(n)={0,1,2,3}?
a) {6,-2+2j-2,-2-2j}
b) {6,-2-2j,2,-2+2j}
c) {6,-2+2j,-2,-2-2j}
d) {6,-2-2j,-2,-2+2j}
View Answer
Explanation: The first step is to determine the matrix W4. By exploiting the periodicity property of W4 and the symmetry property
\(W_{N}^{k+N/2}=-W_{N^k}\)
The matrix W4 may be expressed as
W4=\(\begin{bmatrix}W_4^0&W_4^0&W_4^0&W_4^1\\W_4^0&W_4^0&W_4^2&W_4^3\\W_4^0&W_4^2&W_4^0&W_4^3\\W_4^4&W_4^6&W_4^6&W_4^9\end{bmatrix}=\begin{bmatrix}W_4^0&W_4^0&W_4^0&W_4^1\\W_4^0&W_4^0&W_4^2&W_4^3\\W_4^0&W_4^2&W_4^0&W_4^3\\W_4^0&W_4^2&W_4^2&W_4^1\end{bmatrix}\)
=\(\begin{bmatrix}1&1&1&1\\1&-j&-1&j\\1&-1&1&-1\\1&j&-1&-j\end{bmatrix}\)
Then X4=W4.x4=\(\begin{bmatrix}6\\-2+2j\\-2\\-2-2j\end{bmatrix}\)
8. If X(k) is the N point DFT of a sequence whose Fourier series coefficients is given by ck, then which of the following is true?
a) X(k)=Nck
b) X(k)=ck/N
c) X(k)=N/ck
d) None of the mentioned
View Answer
Explanation: The Fourier series coefficients are given by the expression
ck=\(\frac{1}{N} \sum_{n=0}^{N-1} x(n)e^{-j2πkn/N} = \frac{1}{N}X(k)=> X(k)=Nc_k\)
9. What is the DFT of the four point sequence x(n)={0,1,2,3}?
a) {6,-2+2j-2,-2-2j}
b) {6,-2-2j,2,-2+2j}
c) {6,-2-2j,-2,-2+2j}
d) {6,-2+2j,-2,-2-2j}
View Answer
Explanation: Given x(n)={0,1,2,3}
We know that the 4-point DFT of the above given sequence is given by the expression
X(k)=\(\sum_{n=0}^{N-1} x(n)e^{-j2πkn/N} \)
In this case N=4
=>X(0)=6, X(1)=-2+2j, X(2)=-2, X(3)=-2-2j.
10. If W4100=Wx200, then what is the value of x?
a) 2
b) 4
c) 8
d) 16
View Answer
Explanation: We know that according to the periodicity and symmetry property,
100/4=200/x=>x=8.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice tough questions and answers on all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
