This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “LTI System as Frequency Selective Filters”.
1. An ideal filter should have unity gain in their stop band.
a) True
b) False
View Answer
Explanation: For an ideal filter, in the magnitude response plot at the stop band it should have a sudden fall which means an ideal filter should have a zero gain at stop band.
2. Which filter has a magnitude frequency response as shown in the plot given below?
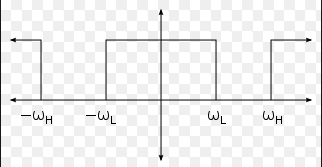
a) Low pass Filter
b) High pass Filter
c) Band pass Filter
d) Band stop Filter
View Answer
Explanation: In the magnitude response shown in the question, the system is stopping a particular band of signals. Hence the filter is called as Band stop filter.
3. An ideal filter should have zero gain in their stop band.
a) True
b) False
View Answer
Explanation: For an ideal filter, in the magnitude response plot at the stop band it should have a sudden fall which means an ideal filter should have a zero gain at stop band.
4. The ‘Envelope delay’ or ‘Group delay’ is the time delay that the signal component of frequency ω undergoes as it passes from the input to the output of the system.
a) True
b) False
View Answer
Explanation: The time delay taken to reach the output of the system from the input by a signal component is called as envelope delay or group delay.
5. If the phase ϴ(ω) of the system is linear, then the group delay of the system?
a) Increases with frequency of signal
b) Constant
c) Decreases with frequency of signal
d) Independent of frequency of signal
View Answer
Explanation: We know that the group delay of the system with phase ϴ(ω) is defined as
Tg(ω)=\(\frac{dϴ(ω)}{dω}\)
Given the phase is linear=> the group delay of the system is constant.
6. A two pole low pass filter has a system function H(z)=\(\frac{b_0}{(1-pz^{-1})^2}\), What is the value of ‘p’ such that the frequency response H(ω) satisfies the condition |H(π/4)|2=1/2 and H(0)=1?
a) 0.46
b) 0.38
c) 0.32
d) 0.36
View Answer
Explanation: Given
H(z)=\(\frac{b_0}{(1-pz^{-1})^2}\) and we know that z=rejω. Here in this case r=1. So z=ejω.
Given at ω=0, H(0)=1=>b0=(1-p)2
Given at ω=π/4, |H(π/4)|2=1/2
=>\(\frac{(1-p)^2}{(1-pe^{-jπ/4})^2}\) = 1/2
=>\(\frac{(1-p)^4}{((1-p/\sqrt 2)^2+p^2/2)^2}\) = 1/2
=> √2(1-p)2=1+p2-√2p
Upon solving the above quadratic equation, we get the value of p as 0.32.
7. A two pole low pass filter has a system function H(z)=\(\frac{b_0}{(1-pz^{-1})^2}\), What is the value of ‘b0‘ such that the frequency response H(ω) satisfies the condition |H(π/4)|2=1/2 and H(0)=1?
a) 0.36
b) 0.38
c) 0.32
d) 0.46
View Answer
Explanation: Given
H(z)=\(\frac{b_0}{(1-pz^{-1})^2}\) and we know that z=rejω. Here in this case r=1. So z=ejω.
Given at ω=0, H(0)=1=>b0=(1-p)2
Given at ω=π/4, |H(π/4)|2=1/2
=>\(\frac{(1-p)^2}{(1-pe^{-jπ/4})^2}\) = 1/2
=>\(\frac{(1-p)^4}{((1-p/\sqrt 2)^2+p^2/2)^2}\) = 1/2
=> √2(1-p)2=1+p2-√2p
Upon solving the above quadratic equation, we get the value of p as 0.32.
Already we have
b0=(1-p)2=(1-0.32)2
=>b0 = 0.46
8. What is the system function for a two pole band pass filter that has the centre of its pass band at ω=π/2, zero its frequency response characteristic at ω=0 and at ω=π, and its magnitude response is 1/√2 at ω=4π/9?
a) \(0.15\frac{1-z^{-2}}{1+0.7z^{-2}}\)
b) \(0.15\frac{1+z^{-2}}{1-0.7z^{-2}}\)
c) \(0.15\frac{1-z^{-2}}{1-0.7z^{-2}}\)
d) \(0.15\frac{1+z^{-2}}{1+0.7z^{-2}}\)
View Answer
Explanation: Clearly, the filter must have poles at P1,2=re±jπ/2 and zeros at z=1 and z=-1. Consequently the system function is
H(z)=\(G\frac{(z-1)(z+1)}{(z-jr)(z+jr)} = G \frac{(z^2-1)}{(z^2+r^2)}\)
The gain factor is determined by evaluating the frequency response H(ω) of the filer at ω=π/2. Thus we have,
H(π/2) = \(G \frac{2}{1-r^2} = 1=>G = \frac{1-r^2}{2}\)
The value of r is determined by evaluating the H(ω) at ω=4π/9. Thus we have
|H(4π/9)|2=\(\frac{(1-r^2)^2}{4}\frac{2-2cos(8π/9)}{1+r^4+2r^2 cos(8π/9)}\)=1/2
On solving the above equation, we get r2=0.7.Therefore the system function for the desired filter is
H(z)=\(0.15\frac{1-z^{-2}}{1+0.7z^{-2}}\)
9. If hlp(n) denotes the impulse response of a low pass filter with frequency response Hlp(ω), then what is the frequency response of the high pass filter in terms of Hlp(ω)?
a) Hlp(ω-π/2)
b) Hlp(ω+π/2)
c) Hlp(ω-π)
d) Hlp(ω+π)
View Answer
Explanation: The impulse response of a high pass filter is simply obtained from the impulse response of the low pass filter by changing the signs of the odd numbered samples in hlp(n). Thus
hhp(n)=(-1)n hlp(n)=(ejπ)n hlp(n)
Thus the frequency response of the high pass filter is obtained as Hlp(ω-π).
10. If the low pass filter described by the difference equation y(n)=0.9y(n-1)+0.1x(n) is converted into a high pass filter, then what is the frequency response of the high pass filter?
a) 0.1/(1+0.9ejω)
b) 0.1/(1+0.9e-jω)
c) 0.1/(1-0.9ejω)
d) None of the mentioned
View Answer
Explanation: The difference equation for the high pass filter is
y(n)=-0.9y(n-1)+0.1x(n)
and its frequency response is given as
H(ω)=0.1/(1+0.9e-jω).
11. A digital resonator is a special two pole band pass filter with the pair of complex conjugate poles located near the unit circle.
a) True
b) False
View Answer
Explanation: The magnitude response of a band pass filter with two complex poles located near the unit circle is as shown below.
The filter gas a large magnitude response at the poles and hence it is called as digital resonator.
12. Which of the following filters have a frequency response as shown below?
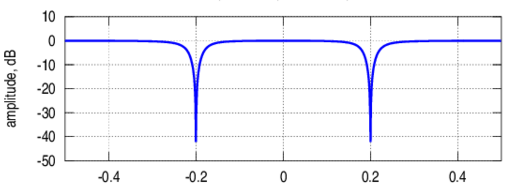
a) Band pass filter
b) Band stop filter
c) All pass filter
d) Notch filter
View Answer
Explanation: The given figure represents the frequency response characteristic of a notch filter with nulls at frequencies at ω0 and ω1.
13. A comb filter is a special case of notch filter in which the nulls occur periodically across the frequency band.
a) True
b) False
View Answer
Explanation: A comb filter can be viewed as a notch filter in which the nulls occur periodically across the frequency band, hence the analogy to an ordinary comb that has periodically spaced teeth.
14. The filter with the system function H(z)=z-k is a ____________
a) Notch filter
b) Band pass filter
c) All pass filter
d) None of the mentioned
View Answer
Explanation: The system with the system function given as H(z)=z-k is a pure delay system. It has a constant gain for all frequencies and hence called as All pass filter.
15. If the system has a impulse response as h(n)=Asin(n+1)ω0u(n), then the system is known as Digital frequency synthesizer.
a) True
b) False
View Answer
Explanation: The given impulse response is h(n)=Asin(n+1)ω0u(n).
According to the above equation, the second order system with complex conjugate poles on the unit circle is a sinusoid and the system is called a digital sinusoidal oscillator or a Digital frequency synthesizer.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
