This set of Digital Signal Processing Multiple Choice Questions & Answers (MCQs) focuses on “FIR Least Squares Inverse Filters”.
1. Wiener filter is an FIR least-squares inverse filter.
a) True
b) False
View Answer
Explanation: FIR least square filters are also called as Wiener filters.
2. If h(n) is the impulse response of an LTI system and hI(n) is the impulse response of the inverse LTI system, then which of the following is true?
a) h(n).hI(n)=1
b) h(n).hI(n)=δ(n)
c) h(n)*hI(n)=1
d) h(n)*hI(n)=δ(n)
View Answer
Explanation: The inverse to a linear time invariant system with impulse response h(n) is defined as the system whose impulse response is hI(n), satisfy the following condition h(n)*hI(n)=δ(n).
3. If H(z) is the system function of an LTI system and HI(z) is the system function of the inverse LTI system, then which of the following is true?
a) H(z)*HI(z)=1
b) H(z)*HI(z)=δ(n)
c) H(z).HI(z)=1
d) H(z).HI(z)=δ(n)
View Answer
Explanation: The inverse to a linear time invariant system with impulse response h(n) and system function H(z) is defined as the system whose impulse response is hI(n) and system function HI(z), satisfy the following condition
H(z).HI(z)=1.
4. It is not desirable to restrict the inverse filter to be FIR.
a) True
b) False
View Answer
Explanation: In most of the practical applications, it is desirable to restrict the inverse filter to be an FIR filter.
5. Which of the following method is used to restrict the inverse filter to be FIR?
a) Truncating hI(n)
b) Expanding hI(n)
c) Truncating HI(z)
d) None of the mentioned
View Answer
Explanation: In many practical applications, it is desirable to restrict the inverse filter to be FIR. One of the simple method to get this requirement is to truncate hI(n).
6. What should be the length of the truncated filter?
a) M
b) M-1
c) M+1
d) Infinite
View Answer
Explanation: In the process of truncating, we incur a total squared approximation error where M+1 is the length of the truncated filter.
7. Which of the following criterion can be used to optimize the M+1 filter coefficients?
a) Pade approximation method
b) Least squares error criterion
c) Least squares error criterion & Pade approximation method
d) None of the mentioned
View Answer
Explanation: We can use the least squares error criterion to optimize the M+1 coefficients of the FIR filter.
8. Which of the following filters have a block diagram as shown in the figure?
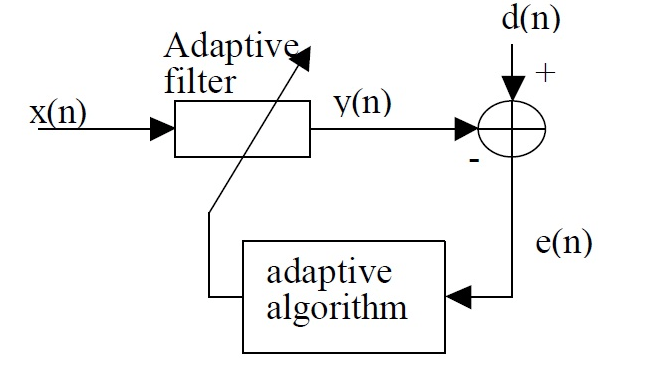
a) Pade wiener filter
b) Pade FIR filter
c) Least squares FIR filter
d) Least squares wiener filter
View Answer
Explanation: Since from the block diagram, the coefficients of the FIR filter coefficients are optimized by the least squares error criterion, it belongs to the least squares FIR inverse filter or wiener filter.
9. The auto correlation of the sequence is required to minimize ε.
a) True
b) False
View Answer
Explanation: When ε is minimized with respect to the filter coefficients, we obtain the set of linear equations which are dependent on the auto correlation sequence of the signal h(n).
10. Which of the following are required to minimize the value of ε?
a) rhh(l)
b) rdh(l)
c) d(n)
d) all of the mentioned
View Answer
Explanation: When ε is minimized with respect to the filter coefficients, we obtain the set of linear equations
\(\sum_{k=0}^M b_k r_{hh}(k-l)=r_{dh} (l)\), l=0,1,…M
and we know that rdh(l) depends on the desired output d(n).
11. FIR filter that satisfies \(\sum_{k=0}^M b_k r_{hh} (k-l)=r_{dh} (l)\), l=0,1,…M is known as wiener filter.
a) True
b) False
View Answer
Explanation: The optimum, in the least square sense, FIR filter that satisfies the linear equations in \(\sum_{k=0}^M b_k r_{hh} (k-l)=r_{dh} (l)\), l=0,1,…M is called the wiener filter.
12. What should be the desired response for an optimum wiener filter to be an approximate inverse filter?
a) u(n)
b) δ(n)
c) u(-n)
d) none of the mentioned
View Answer
Explanation: If the optimum least squares FIR filter is to be an approximate inverse filter, the desired response is
d(n)=δ(n).
13. If the set of linear equations from the equation \(\sum_{k=0}^M b_k r_{hh} (k-l)=r_{dh} (l)\), l=0,1,…M are expressed in matrix form, then what is the type of matrix obtained?
a) Symmetric matrix
b) Skew symmetric matrix
c) Toeplitz matrix
d) Triangular matrix
View Answer
Explanation: We observe that the matrix is not only symmetric but it also has the special property that all the elements along any diagonal are equal. Such a matrix is called a Toeplitz matrix and lends itself to efficient inversion by means of an algorithm.
14. What is the number of computations proportional to, in Levinson-Durbin algorithm?
a) M
b) M2
c) M3
d) M1/2
View Answer
Explanation: The Levinson-Durbin algorithm is the algorithm which is used for the efficient inversion of Toeplitz matrix which requires a number of computations proportional to M2 instead of the usual M3.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
