This set of Digital Signal Processing Questions & Answers for experienced focuses on “Structures for FIR Systems”.
1. Which of the following is the application of lattice filter?
a) Digital speech processing
b) Adaptive filter
c) Electroencephalogram
d) All of the mentioned
View Answer
Explanation: Lattice filters are used extensively in digital signal processing and in the implementation of adaptive filters.
2. If we consider a sequence of FIR filer with system function Hm(z)=Am(z), then what is the definition of the polynomial Am(z)?
a) \(1+\sum_{k=0}^m α_m (k)z^{-k}\)
b) \(1+\sum_{k=1}^m α_m (k)z^{-k}\)
c) \(1+\sum_{k=1}^m α_m (k)z^k \)
d) \(\sum_{k=0}^m α_m (k)z^{-k}\)
View Answer
Explanation: Consider a sequence of FIR filer with system function Hm(z)=Am(z), m=0,1,2…M-1
where, by definition, Am(z) is the polynomial
Am(z)=\(1+\sum_{k=1}^m α_m (k)z^{-k}\), m≥1 and A0(z)=1.
3. What is the unit sample response of the mth filter?
a) hm(0)=0 and hm(k)=αm(k), k=1,2…m
b) hm(k)=αm(k), k=0,1,2…m(αm(0)≠1)
c) hm(0)=1 and hm(k)=αm(k), k=1,2…m
d) none of the mentioned
View Answer
Explanation: We know that Hm(z)=Am(z) and Am(z) is a polynomial whose equation is given as Am(z)=\(1+\sum_{k=1}^m α_m (k)z^{-k}\), m≤1 and A0(z)=1
A0(z)=1 => hm(0)=1 and Am(z)=\(\sum_{k=1}^m α_m (k)z^{-k}\)(m≤1)=> hm(k)=αm(k) for k=1,2…m.
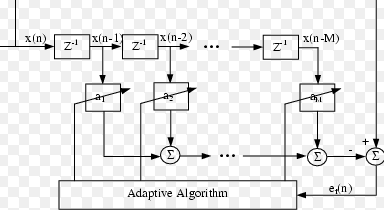
4. The FIR filter whose direct form structure is as shown below is a prediction error filter.
a) True
b) False
View Answer
Explanation: The FIR structure shown in the above figure is intimately related with the topic of linear prediction. Thus the top filter structure shown in the above figure is called a prediction error filter.
5. What is the output of the single stage lattice filter if x(n) is the input?
a) x(n)+Kx(n+1)
b) x(n)+Kx(n-1)
c) x(n)+Kx(n-1)+Kx(n+1)
d) Kx(n-1)
View Answer
Explanation: The single stage lattice filter is as shown below.
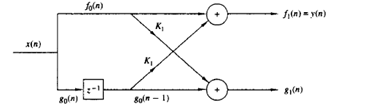
Here both the inputs are excited and output is selected from the top branch.
Thus the output of the single stage lattice filter is given by y(n)= x(n)+Kx(n-1).
6. What is the output from the second stage lattice filter when two single stage lattice filers are cascaded with an input of x(n)?
a) K1K2x(n-1)+K2x(n-2)
b) x(n)+K1x(n-1)
c) x(n)+K1K2x(n-1)+K2x(n-2)
d) x(n)+K1(1+K2)x(n-1)+K2x(n-2)
View Answer
Explanation: When two single stage lattice filters are cascaded, then the output from the first filter is given by the equation
f1(n)= x(n)+K1x(n-1)
g1(n)=K1x(n)+x(n-1)
The output from the second filter is obtained as
f2(n)=f1(n)+K2g1(n-1)
=x(n)+K2[K1x(n-1)+x(n-2)]+ K1x(n-1)
= x(n)+K1(1+K2)x(n-1)+K2x(n-2).
7. What is the value of the coefficient α2(1) in the case of FIR filter represented in direct form structure with m=2 in terms of K1 and K2?
a) K1(K2)
b) K1(1-K2)
c) K1(1+K2)
d) None of the mentioned
View Answer
Explanation: The equation for the output of an FIR filter represented in the direct form structure is given as
y(n)=x(n)+ α2(1)x(n-1)+ α2(2)x(n-2)
The output from the double stage lattice structure is given by the equation,
f2(n)= x(n)+K2(1+K2)x(n-1)+K2x(n-2)
By comparing the coefficients of both the equations, we get
α2(1)= K1(1+K2).
8. The constants K1 and K2 of the lattice structure are called as reflection coefficients.
a) True
b) False
View Answer
Explanation: The equation of the output from the second stage lattice filter is given by
f2(n)= x(n)+K1(1+K2)x(n-1)+K2x(n-2)
In the above equation, the constants K1 and K2 are called as reflection coefficients.
9. If a three stage lattice filter with coefficients K1=1/4, K2=1/2 K3=1/3, then what are the FIR filter coefficients for the direct form structure?
a) (1,8/24,5/8,1/3)
b) (1,5/8,13/24,1/3)
c) (1/4,13/24,5/8,1/3)
d) (1,13/24,5/8,1/3)
View Answer
Explanation: We get the output from the third stage lattice filter as
A3(z)=1+(13/24)z-1+(5/8)z-2+(1/3)z-3.
Thus the FIR filter coefficients for the direct form structure are (1,13/24,5/8,1/3).
10. What are the lattice coefficients corresponding to the FIR filter with system function H(z)= 1+(13/24)z-1+(5/8)z-2+(1/3)z-3?
a) (1/2,1/4,1/3)
b) (1,1/2,1/3)
c) (1/4,1/2,1/3)
d) None of the mentioned
View Answer
Explanation: Given the system function of the FIR filter is
H(z)= 1+(13/24)z-1+(5/8)z-2+(1/3)z-3
Thus the lattice coefficients corresponding to the given filter is (1/4,1/2,1/3).
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing for experienced, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
