Binary Search Tree in C

Problem Description

Write a C program to implement the Binary Search Tree operations and display its traversals.

Outline of a Binary Search Tree:

What is a Tree?
What is a Binary Tree?
What is a Binary Search Tree?
Doubly Linked List Representation of a BST Node
Implementation of Binary Search Tree (Program/Code)
Binary Search Tree – insert() Method
Binary Search Tree – delete() Method
Binary Search Tree – search() Method
Traversals of the Binary Search Tree

Inorder Traversal
Preorder Traversal
Postorder Traversal

What is a Tree?

A tree is a non-linear data structure in which the data is stored non-linearly. A tree is used to represent the data in hierarchical form. It has a collection of objects that store data into its which is known as nodes.

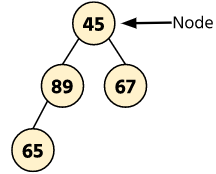
The above image represents a tree in which four nodes are connected in a hierarchical structure. Every node contains some integer data and the address of its children.

Now, before going to understand the binary search tree let’s take a look at the binary tree and its representation.

What is a Binary Tree?

A binary tree is a kind of tree in which every node contains at most two children. A node contains the address of the left and right child in the linked list representation of the binary tree.

If a node does not contain either child, its field will be NULL. If there are no children for that node then it is called the Leaf node.

Subscribe Now: Data Structures in C Newsletter | Important Subjects Newsletters

What is a Binary Search Tree?

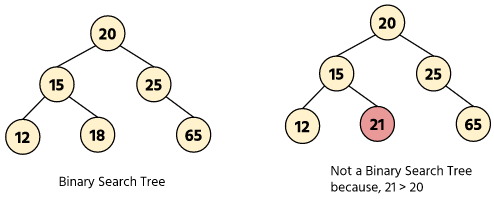
A binary Search Tree is a special tree in which some order is followed. Every parent node has at most two children in which the left children have a lesser value while the right children have a higher value than their parent. This rule is applied to all left and right subtrees.

Problem Solution

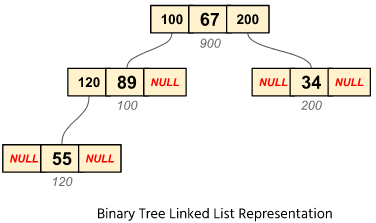
We will implement the binary search tree using the doubly linked list. A doubly linked list contains the address of the left and right children and the data of the node. The left pointer of the node points to the left children and the right pointer points to the right children.

Here is the representation of a node using a doubly linked list.

struct node
{
	int data;
	struct node* left;
struct node* right;
};

Doubly Linked List representation of a BST node:

left*

data

right*

Program/Source Code

Here is the source code of the C program to implement the Binary Search Tree operations. The C program is successfully compiled and run on a Linux system. The program output is also shown below.

```
/*
```

* C program to implement the Binary Search Tree

```
*/
```
```
#include <stdio.h>
```
```
#include <stdlib.h>
```
```
 
```
```
// structure of a node
```
```
struct node
```
```
{
```
```
    int data;
```
```
    struct node *left;
```
```
    struct node *right;
```
```
};
```
```
 
```
```
// globally initialized root pointer
```
```
struct node *root = NULL;
```
```
 
```
```
// function prototyping
```
```
struct node *create_node(int);
```
```
void insert(int);
```

struct node *delete (struct node *, int);

```
int search(int);
```
```
void inorder(struct node *);
```
```
void postorder();
```
```
void preorder();
```

struct node *smallest_node(struct node *);

struct node *largest_node(struct node *);

```
int get_data();
```
```
 
```
```
int main()
```
```
{
```
```
    int userChoice;
```
```
    int userActive = 'Y';
```
```
    int data;
```
```
    struct node* result = NULL;
```
```
 
```

    while (userActive == 'Y' || userActive == 'y')

```
    {
```

        printf("\n\n------- Binary Search Tree ------\n");

```
        printf("\n1. Insert");
```
```
        printf("\n2. Delete");
```
```
        printf("\n3. Search");
```

        printf("\n4. Get Larger Node Data");

        printf("\n5. Get smaller Node data");

```
        printf("\n\n-- Traversals --");
```
```
        printf("\n\n6. Inorder ");
```
```
        printf("\n7. Post Order ");
```
```
        printf("\n8. Pre Oder ");
```
```
        printf("\n9. Exit");
```
```
 
```

        printf("\n\nEnter Your Choice: ");

```
        scanf("%d", &userChoice);
```
```
        printf("\n");
```
```
 
```
```
        switch(userChoice)
```
```
        {
```
```
            case 1:
```
```
                data = get_data();
```
```
                insert(data);
```
```
                break;
```
```
 
```
```
            case 2:
```
```
                data = get_data();
```

                root = delete(root, data);

```
                break;
```
```
 
```
```
            case 3:
```
```
                data = get_data();
```
```
                if (search(data) == 1)
```
```
                {
```

                    printf("\nData was found!\n");

```
                }
```
```
                else
```
```
                {
```

                    printf("\nData does not found!\n");

```
                }
```
```
                break;
```
```
 
```
```
            case 4:
```

                result = largest_node(root);

```
                if (result != NULL)
```
```
                {
```

                    printf("\nLargest Data: %d\n", result->data);

```
                }
```
```
                break;
```
```
 
```
```
            case 5:
```

                result = smallest_node(root);

```
                if (result != NULL)
```
```
                {
```

                    printf("\nSmallest Data: %d\n", result->data);

```
                }
```
```
                break;
```
```
 
```
```
            case 6:
```
```
                inorder(root);
```
```
                break;
```
```
 
```
```
            case 7:
```
```
                postorder(root);
```
```
                break;
```
```
 
```
```
            case 8:
```
```
                preorder(root);
```
```
                break;
```
```
 
```
```
            case 9:
```

                printf("\n\nProgram was terminated\n");

```
                break;
```
```
 
```
```
            default:
```

                printf("\n\tInvalid Choice\n");

```
                break;
```
```
        }
```
```
 
```

        printf("\n__________\nDo you want to continue? ");

```
        fflush(stdin);
```
```
        scanf(" %c", &userActive);
```
```
    }
```
```
 
```
```
    return 0;
```
```
}
```
```
 
```
```
// creates a new node
```
```
struct node *create_node(int data)
```
```
{
```

    struct node *new_node = (struct node *)malloc(sizeof(struct node));

```
 
```
```
    if (new_node == NULL)
```
```
    {
```

        printf("\nMemory for new node can't be allocated");

```
        return NULL;
```
```
    }
```
```
 
```
```
    new_node->data = data;
```
```
    new_node->left = NULL;
```
```
    new_node->right = NULL;
```
```
 
```
```
    return new_node;
```
```
}
```
```
 
```
```
// inserts the data in the BST
```
```
void insert(int data)
```
```
{
```

    struct node *new_node = create_node(data);

```
 
```
```
    if (new_node != NULL)
```
```
    {
```

        // if the root is empty then make a new node as the root node

```
        if (root == NULL)
```
```
        {
```
```
            root = new_node;
```

            printf("\n* node having data %d was inserted\n", data);

```
            return;
```
```
        }
```
```
 
```
```
        struct node *temp = root;
```
```
        struct node *prev = NULL;
```
```
 
```

        // traverse through the BST to get the correct position for insertion

```
        while (temp != NULL)
```
```
        {
```
```
            prev = temp;
```
```
            if (data > temp->data)
```
```
            {
```
```
                temp = temp->right;
```
```
            }
```
```
            else
```
```
            {
```
```
                temp = temp->left;
```
```
            }
```
```
        }
```
```
 
```

        // found the last node where the new node should insert

```
        if (data > prev->data)
```
```
        {
```
```
            prev->right = new_node;
```
```
        }
```
```
        else
```
```
        {
```
```
            prev->left = new_node;
```
```
        }
```
```
 
```

        printf("\n* node having data %d was inserted\n", data);

```
    }
```
```
}
```
```
 
```

// deletes the given key node from the BST

struct node *delete (struct node *root, int key)

```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return root;
```
```
    }
```
```
    if (key < root->data)
```
```
    {
```

        root->left = delete (root->left, key);

```
    }
```
```
    else if (key > root->data)
```
```
    {
```

        root->right = delete (root->right, key);

```
    }
```
```
    else
```
```
    {
```
```
        if (root->left == NULL)
```
```
        {
```

            struct node *temp = root->right;

```
            free(root);
```
```
            return temp;
```
```
        }
```
```
        else if (root->right == NULL)
```
```
        {
```

            struct node *temp = root->left;

```
            free(root);
```
```
            return temp;
```
```
        }
```

        struct node *temp = smallest_node(root->right);

```
        root->data = temp->data;
```

        root->right = delete (root->right, temp->data);

```
    }
```
```
    return root;
```
```
 
```
```
}
```
```
 
```
```
// search the given key node in BST
```
```
int search(int key)
```
```
{
```
```
    struct node *temp = root;
```
```
 
```
```
    while (temp != NULL)
```
```
    {
```
```
        if (key == temp->data)
```
```
        {
```
```
            return 1;
```
```
        }
```
```
        else if (key > temp->data)
```
```
        {
```
```
            temp = temp->right;
```
```
        }
```
```
        else
```
```
        {
```
```
            temp = temp->left;
```
```
        }
```
```
    }
```
```
    return 0;
```
```
}
```
```
 
```

// finds the node with the smallest value in BST

struct node *smallest_node(struct node *root)

```
{
```
```
    struct node *curr = root;
```

    while (curr != NULL && curr->left != NULL)

```
   {
```
```
        curr = curr->left;
```
```
    }
```
```
    return curr;
```
```
}
```
```
 
```

// finds the node with the largest value in BST

struct node *largest_node(struct node *root)

```
{
```
```
    struct node *curr = root;
```

    while (curr != NULL && curr->right != NULL)

```
    {
```
```
        curr = curr->right;
```
```
    }
```
```
    return curr;
```
```
}
```
```
 
```
```
// inorder traversal of the BST
```
```
void inorder(struct node *root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
    inorder(root->left);
```
```
    printf("%d ",  root->data);
```
```
    inorder(root->right);
```
```
}
```
```
 
```
```
// preorder traversal of the BST
```
```
void preorder(struct node *root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
    printf("%d ", root->data);
```
```
    preorder(root->left);
```
```
    preorder(root->right);
```
```
}
```
```
 
```
```
// postorder travsersal of the BST
```
```
void postorder(struct node *root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
    postorder(root->left);
```
```
    postorder(root->right);
```
```
    printf("%d ", root->data);
```
```
}
```
```
 
```
```
// getting data from the user
```
```
int get_data()
```
```
{
```
```
    int data;
```
```
    printf("\nEnter Data: ");
```
```
    scanf("%d", &data);
```
```
    return data;
```
```
}
```

Program Explanation

Here we have discussed the main functions of the Binary Search Tree with time and space complexities.

Insert a new Node – insert() method

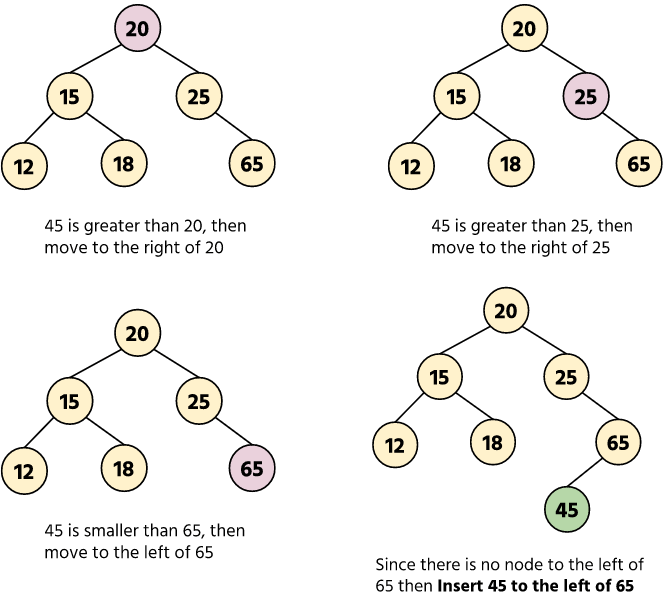
To insert the new node, we have to follow the given steps:

Find the node where the new node has to be inserted and store the visited node in the temp variable.
Now, the new node data will be compared with temp.
If the data is larger than temp data then insert the new node at the right of the temp.
If the data is smaller then insert the new node at the left of the temp.

Example: Let’s insert the new node 45 in the given Binary Search Tree. We have the following steps to insert it in the right position.

Time Complexity:
Worst Case: O(n)
When the binary search tree becomes a skewed tree then we need to traverse each node so the time complexity becomes O(n), where n is the number of nodes.

Best and Average Case: O(h)
In general, we need to traverse the tree up to h height, so the complex becomes O(h), where h is the height of the tree.

Space Complexity: O(1)
Space is constant in this method since we are using only temporary variables.

Run Time Testcases

In this case, we are inserting the nodes in binary search tree.

------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 20
* node having data 20 was inserted
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 15
* node having data 15 was inserted
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 25
* node having data 25 was inserted
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 12
* node having data 12 was inserted
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 18
* node having data 18 was inserted
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 1
Enter Data: 65
* node having data 65 was inserted
__________
Do you want to continue? n

Delete a Node – delete() Method

There are three cases to delete the node from the tree. Let’s discuss all the cases using the examples that are given below.

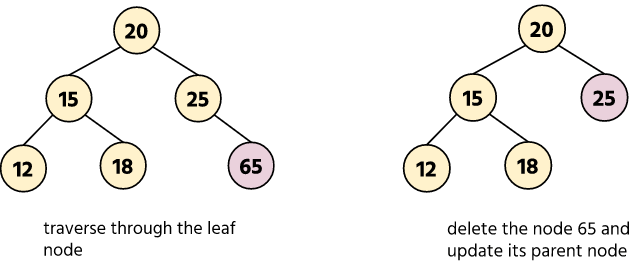
case 1: Deleting the leaf node
To delete the leaf node we need to traverse to the required leaf node then delete that node and update its parent.

Example: Deleting a leaf node 65.

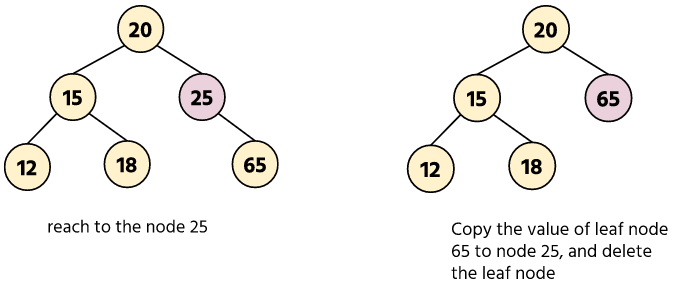
case 2: Delete a node with one child
Remove that given node and replace it with its children.

Example: Deleting node 25, to delete node 25, we have to update it with its children node 65.

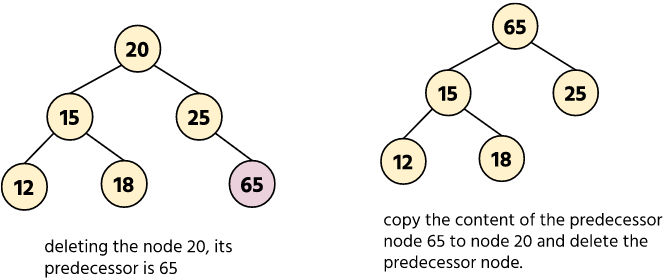
case 3: Deleting a node with two children
In this case, find the inorder successor of the node to which it is deleting. Copy the content of the inorder successor node to the node. Delete the inorder successor. For this case, we can also use the inorder predecessor.

Example: Deleting node 20 from the given tree.

Time Complexity:
Worst Case: O(n)
In this case the tree is a skewed tree. So we need to traverse each node.

Best and Average Case: O(h)
In general, the time complexity depends on the height(h) of the BST.

Space Complexity: O(n)
Where n is the number of nodes in the BST. In the worst case the calling stack of the node calls the total number of nodes.

Run Time Testcases

In this case, we are deleting the nodes in binary search tree.
Note: The data in the Binary Search Tree are {12 15 18 20 25 65}

------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 6
12 15 18 20 25 65 
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 2
Enter Data: 25
__________
Do you want to continue? y
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 6
12 15 18 20 65 
__________
Do you want to continue? n

Search a Node – search() method

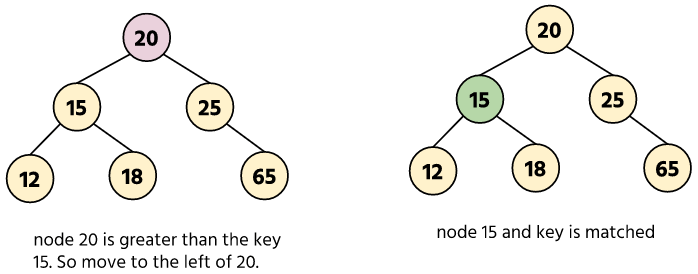
Searching a node in a Binary search tree takes the following steps:

Compare the current node data with the key if:

If the key is found, then return the node.
If the key is lesser than the node data, move the current to the left node and again repeat step 1.
If the key is greater then move to the right and repeat step 1.

If the node is not found then return NULL.

Example: Let’s find the node with data 15 in the given BST.

Time Complexity:
Worst Case: O(n)
In the worst case, we have to traverse each node. Here n is the number of nodes in the binary search tree.

Best Case and Average Case: O(h)
In this case, the complexity depends on the height h of the binary search tree.

Space Complexity: O(1)
Space is constant in this method since we are using only temporary variables.

Run Time Testcases

In this case, we are searching the nodes in binary search tree.
Note: The data in the Binary Search Tree are {12 15 18 20 25 65}

------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 3
Enter Data: 65
Data was found!
__________
Do you want to continue? y
 
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 3
Enter Data: 64
Data does not found!
__________
Do you want to continue? y
 
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 4
Largest Data: 65
_________
Do you want to continue? y
 
------- Binary Search Tree ------
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 5
Smallest Data: 12
 
__________
Do you want to continue?

Traversals of the Binary Search Tree

Inorder Traversal

In inorder traversal, we have to traverse in the following order:

Traverse to the left to a given node.
print the node data.
Traverse to the right to a given node.

Example: Inorder traversal of the tree is given below.

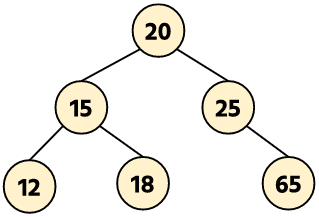
Inorder: 12, 15, 18, 20, 25, 65

Time Complexity: O(n)
Here, n is the number of nodes. We have to traverse each node in the BST.

Space Complexity: O(h)
The height of the skewed binary search tree is the number of nodes.

Run Time Testcases

In this case, we perform an in-order traversal of the binary search tree.
Note: The data in the Binary Search Tree are {12 15 18 20 25 65}

------- Binary Search Tree ------
 
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 6
12 15 18 20 25 65 
__________
Do you want to continue? n

Preorder Traversal

In preorder traversal, we have to traverse in the following order:

Print the node data.
Traverse to the left to a given node.
Traverse to the right to a given node.

Example: Preorder traversal of the binary search tree is given below.

Preorder: 20, 15, 12, 18, 25, 65

Time Complexity: O(n)
Here, n is the number of nodes. We have to traverse each node in the BST.

Space Complexity: O(h)
The height of the skewed binary search tree is the number of nodes.

Run Time Testcases

In this case, we perform an pre-order traversal of the binary search tree.
Note: The data in the Binary Search Tree are {12 15 18 20 25 65}

------- Binary Search Tree ------
 
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 8
20 15 12 18 25 65 
__________
Do you want to continue? n

Postorder Traversal

In preorder traversal, we have to traverse in the following order:

Traverse to the left to a given node.
Traverse to the right to a given node.
Print the data of the node.

Example: Postorder traversal of the binary search tree is given below.

Postorder: 12, 18, 15, 65, 25, 20

Time Complexity: O(n)
Here, n is the number of nodes. We have to traverse each node in the BST.

Space Complexity: O(h)
The height of the skewed binary search tree is the number of nodes.

Run Time Testcases

In this case, we perform an post-order traversal of the binary search tree.
Note: The data in the Binary Search Tree are {12 15 18 20 25 65}

------- Binary Search Tree ------
 
1. Insert
2. Delete
3. Search
4. Get Larger Node Data
5. Get smaller Node data
 
-- Traversals --
 
6. Inorder 
7. Post Order 
8. Pre Oder 
9. Exit
 
Enter Your Choice: 7
12 18 15 65 25 20 
__________
Do you want to continue? n

To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.

If you find any mistake above, kindly email to [email protected]

« Prev - C Program to Implement Doubly Linked List using Singly Linked List

» Next - C Program to Implement External Sorting using B Tree and Inorder Traversal

Related Posts:

Practice Programming MCQs
Apply for Computer Science Internship
Practice Design & Analysis of Algorithms MCQ
Check Programming Books
Practice Computer Science MCQs

Recommended Articles: