Binary Tree Program in C

Problem Description

Write a C program to implement the Binary Tree operations and display its traversals.

Outline of a Binary Search Tree:

What is a Tree?
What is a Binary Tree?
Doubly Linked List Representation of a Binary Tree Node
Implementation of Binary Tree (Program/Code)
Binary Tree – insert() Method
Binary Tree – delete() Method
Binary Tree – search() Method
Traversals of the Binary Tree

Inorder Traversal
Preorder Traversal
Postorder Traversal

What is a Tree?

A tree is a non-linear data structure in which the data is stored non-linearly. A tree is used to represent the data in hierarchical form.

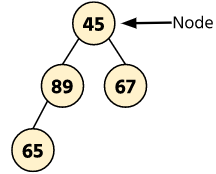
The above image represents a tree in which four nodes are connected in a hierarchical structure. Every node contains some integer data and the address of its children.

What is a Binary Tree?

A binary tree is a kind of tree in which every node contains at most two children. A node contains the address of the left and right child in the linked list representation of the binary tree.

If a node does not contain either child, its field will be NULL. If there are no children for that node then it is called the Leaf node.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

Problem Solution

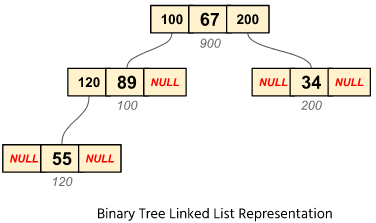
We will implement the binary tree using the doubly linked list. A doubly linked list contains the address of the left and right children and the data of the node. The left pointer of the node points to the left children and the right pointer points to the right children.

Here is the representation of a node using a doubly linked list.

struct node
{
	int data;
	struct node* left;
        struct node* right;
};

Doubly Linked List representation of a Binary Tree node:

left*

data

right*

Program/Source Code

Here is the source code of the C program to implement the Binary Tree. The C program is successfully compiled and run on a Linux system. The program output is also shown below.

```
/*
```

 * C Program to Implement the Binary Tree

```
 */
```
```
 
```
```
#include<stdio.h>
```
```
#include<stdlib.h>
```
```
#define MAX_SIZE 25
```
```
#define max(a, b) a>b ? a : b
```
```
 
```
```
struct TreeNode
```
```
{
```
```
    int val;
```
```
    struct TreeNode* left;
```
```
    struct TreeNode* right;
```
```
};
```
```
 
```
```
// global root declaration
```
```
struct TreeNode* root = NULL;
```
```
 
```
```
// function prototyping
```
```
void insert(int);
```
```
void delete(int);
```
```
int search(int);
```
```
int height(struct TreeNode*);
```
```
void inorder(struct TreeNode*);
```
```
void preorder(struct TreeNode*);
```
```
void postorder(struct TreeNode*);
```
```
void levelorder();
```
```
 
```
```
int main()
```
```
{
```
```
    int user_choice, node_data;
```
```
    char user_active = 'Y';
```
```
 
```

    while(user_active == 'Y' || user_active == 'y')

```
    {
```

        printf("\n\n--- Binary Tree --\n\n");

```
        printf("\n1. Insert ");
```
```
        printf("\n2. Delete");
```
```
        printf("\n3. Search");
```
```
        printf("\n4. Height");
```

        printf("\n5. Inorder Traversal");

        printf("\n6. Preorder Traversal");

        printf("\n7. Postorder Traversal");

        printf("\n8. Level order Traversal");

```
        printf("\n9. Exit");
```

        printf("\n\nEnter Your Choice: ");

```
        scanf("%d", &user_choice);
```
```
 
```
```
        printf("\n");
```
```
        switch(user_choice)
```
```
        {
```
```
            case 1:
```

                printf("Enter data for new node: ");

                scanf("%d", &node_data);

```
                insert(node_data);
```
```
                break;
```
```
 
```
```
            case 2:
```

                printf("Enter node data: ");

                scanf("%d", &node_data);

```
                delete(node_data);
```
```
                break;
```
```
 
```
```
            case 3: 
```

                printf("Enter node data: ");

                scanf("%d", &node_data);

                int has_found = search(node_data);

```
 
```
```
                if(has_found == -1) {
```

                    printf("\nNode was not found!");

```
                } else {
```

                    printf("\nNode was found");

```
                }
```
```
                break;
```
```
 
```
```
            case 4: 
```

                printf("height of the tree is: %d", height(root));

```
                break;
```
```
 
```
```
            case 5: 
```

                printf("Inorder Traversal\n\n");

```
                inorder(root);
```
```
                break;
```
```
 
```
```
            case 6: 
```

                printf("Preorder Traversal\n\n");

```
                preorder(root);
```
```
                break;
```
```
 
```
```
            case 7: 
```

                printf("Postorder Traversal\n\n");

```
                postorder(root);
```
```
                break;
```
```
 
```
```
            case 8:
```

                printf("Level order Traversal\n\n");

```
                levelorder();
```
```
                break;
```
```
 
```
```
            case 9:
```

                printf("Program is terminating...\n\n");

```
                exit(0);
```
```
 
```
```
            default:
```

                printf("Invalid choice");

```
        }
```
```
 
```
```
        fflush(stdin);
```

        printf("\n\n\nDo you want to continue? (Y/N) ");

```
        scanf("%c", &user_active);
```
```
    }
```
```
    return 0;
```
```
}
```
```
 
```
```
struct TreeNode* create(int data)
```
```
{
```

    struct TreeNode* new_node = (struct TreeNode*) malloc (sizeof(struct TreeNode));

```
    if(new_node == NULL)
```
```
    {
```

        printf("\nMemory can't be allocated for new node\n");

```
        return NULL;
```
```
    }
```
```
 
```
```
    new_node->left = NULL;
```
```
    new_node->right = NULL;
```
```
    new_node->val = data;
```
```
 
```
```
    return new_node;
```
```
}
```
```
 
```
```
// inserts a new node in the tree
```
```
void insert(int data)
```
```
{
```
```
    if(root == NULL)
```
```
    {
```

        struct TreeNode* new_node = create(data);

```
        if(new_node)
```
```
        {
```
```
            root = new_node;
```

            printf("\n * Node with data %d was inserted", data);

```
        }
```
```
        return;
```
```
    }
```
```
 
```
```
    struct TreeNode* queue[MAX_SIZE];
```
```
    struct TreeNode* new_node = NULL;
```
```
    int front = -1;
```
```
    int rear = -1;
```
```
    queue[front+1] = root;
```
```
    front = rear = 0;
```
```
 
```
```
    while(front <= rear)
```
```
    {
```

        struct TreeNode* temp = queue[front];

```
        front++;
```
```
 
```
```
        if(temp->left != NULL)
```
```
        {
```
```
            queue[++rear] = temp->left;
```
```
        }
```
```
        else
```
```
        {
```
```
            new_node = create(data);
```
```
            if(new_node)
```
```
            {
```
```
                temp->left = new_node;
```

                printf("\n* Node with data %d was inserted", data);

```
            }
```
```
            return;
```
```
        }
```
```
 
```
```
        if(temp->right != NULL)
```
```
        {
```

            queue[++rear] = temp->right;

```
        }
```
```
        else
```
```
        {
```
```
            new_node = create(data);
```
```
            if(new_node)
```
```
            {
```
```
                temp->right = new_node;
```

                printf("\n* Node with data %d was inserted", data);

```
            }
```
```
            return;
```
```
        }
```
```
    }
```
```
}
```
```
 
```
```
void delete(int key)
```
```
{
```
```
    // Tree is empty
```
```
    if(root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
 
```
```
    // Tree having only one node
```

    if(root->left == NULL && root->right == NULL)

```
    {
```
```
        if(root->val == key)
```
```
        {
```
```
            root = NULL;
```

            printf("\n* Node with data %d was deleted", key);

```
            return;
```
```
        }
```
```
        else
```
```
        {
```
```
            return;
```
```
        }
```
```
    }
```
```
 
```

    // level order traversal using the queue

    struct TreeNode* temp = NULL, *last_node = NULL, *key_node = NULL;

```
 
```
```
    struct TreeNode* queue[MAX_SIZE];
```
```
    int front = -1;
```
```
    int rear = -1;
```
```
 
```
```
    queue[front + 1] = root;
```
```
    front = rear = 0;
```
```
 
```

    // do level order traversal to find the deepest node

```
    while (front <= rear)
```
```
    {
```
```
        temp = queue[front];
```
```
        front++;
```
```
 
```
```
        if (temp->val == key)
```
```
        {
```
```
            key_node = temp;
```
```
        }
```
```
 
```
```
        if (temp->left != NULL)
```
```
        {
```
```
            last_node = temp;
```
```
            queue[++rear] = temp->left;
```
```
        }
```
```
 
```
```
        if (temp->right != NULL)
```
```
        {
```
```
            last_node = temp;
```

            queue[++rear] = temp->right;

```
        }
```
```
    }
```
```
 
```

    // if key is found in the binary tree

```
    if (key_node != NULL)
```
```
    {
```

        // replace the keynode data with the deepest node

```
        key_node->val = temp->val;
```
```
 
```

        // free the last node after updating its parent

```
        if (last_node->right == temp)
```
```
        {
```
```
            last_node->right = NULL;
```
```
        }
```
```
        else
```
```
        {
```
```
            last_node->left = NULL;
```
```
        }
```

        printf("\n* Node with data %d was deleted", key);

```
        free(temp);
```
```
        return;
```
```
    }
```

    printf("\n* Node with data %d was not found", key);

```
}   
```
```
 
```
```
int search(int key)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return -1;
```
```
    }
```
```
    struct TreeNode* queue[MAX_SIZE];
```
```
    int front = -1;
```
```
    int rear = -1;
```
```
 
```
```
    queue[front + 1] = root;
```
```
    front = rear = 0;
```
```
 
```

    // do level order traversal to find the deepest node

```
    while (front <= rear)
```
```
    {
```

        struct TreeNode* temp = queue[front];

```
        front++;
```
```
 
```
```
        if (temp->val == key)
```
```
        {
```
```
            return 1;
```
```
        }
```
```
 
```
```
        if (temp->left != NULL)
```
```
        {
```
```
            queue[++rear] = temp->left;
```
```
        }
```
```
 
```
```
        if (temp->right != NULL)
```
```
        {
```

            queue[++rear] = temp->right;

```
        }
```
```
    }
```
```
    return -1;
```
```
}
```
```
 
```
```
int height(struct TreeNode* root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return 0;
```
```
    }
```
```
 
```
```
    int left = height(root->left);
```
```
    int right = height(root->right);
```
```
 
```
```
    if(left > right)
```
```
    {
```
```
        return left + 1;
```
```
    }
```
```
    else
```
```
    {
```
```
        return right + 1;
```
```
    }
```
```
}
```
```
 
```
```
// inorder traversal
```
```
void inorder(struct TreeNode* root)
```
```
{
```
```
    if(root == NULL) return;
```
```
 
```
```
    inorder(root->left);
```
```
    printf("%d ", root->val);
```
```
    inorder(root->right);
```
```
}
```
```
 
```
```
// preorder traversal
```
```
void preorder(struct TreeNode* root)
```
```
{
```
```
    if(root == NULL) return;
```
```
 
```
```
    printf("%d ", root->val);
```
```
    preorder(root->left);
```
```
    preorder(root->right);
```
```
}
```
```
 
```
```
// postorder traversal
```
```
void postorder(struct TreeNode* root)
```
```
{
```
```
    if(root == NULL) return;
```
```
 
```
```
    postorder(root->left);
```
```
    postorder(root->right);
```
```
    printf("%d ", root->val);
```
```
}
```
```
 
```
```
// level order traversal
```
```
void levelorder()
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        printf("Tree is Empty!");
```
```
        return;
```
```
    }
```
```
 
```
```
    struct TreeNode* queue[MAX_SIZE];
```
```
    int front = -1;
```
```
    int rear = -1;
```
```
 
```
```
    queue[front + 1] = root;
```
```
    front = rear = 0;
```
```
 
```

    // do level order traversal to find the deepest node

```
    while (front <= rear)
```
```
    {
```

        struct TreeNode* temp = queue[front];

```
        front++;
```
```
 
```
```
        printf("%d ", temp->val);
```
```
 
```
```
        if (temp->left != NULL)
```
```
        {
```
```
            queue[++rear] = temp->left;
```
```
        }
```
```
 
```
```
        if (temp->right != NULL)
```
```
        {
```

            queue[++rear] = temp->right;

```
        }
```
```
    }
```
```
}
```

Program Explanation

Here we have discussed the main functions of the Binary Tree with time and space complexities.

Insert a New Node in the Binary Tree

Insertion is the method to add a new node in the Binary Tree. We are traversing the binary tree in level order so that we can balance the binary tree on insertion at each level.

Start traversing the tree from the root node in level order.
Insert the node at the left children of a node, If the left child of a node is NULL.
If the left child is not NULL then check for the right child, Insert the node at the right of the node.
Exit.

Example: Let’s insert the given nodes in the Binary Tree.
Nodes = [89, 56, 45, 2, 55]

Step 1: Insert a new node 89.

Step 2: Insert a new node 56.

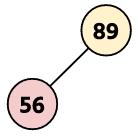
Step 3: Insert a new node 45.

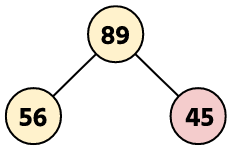
Step 4: Insert a new node 2.

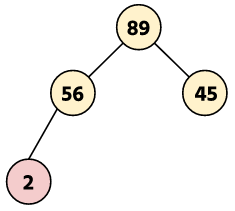
Step 5: Insert a new node 55.

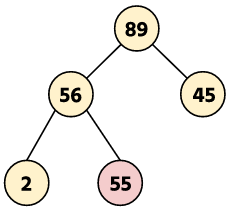
Time Complexity: O(n)
We need to traverse each node in level order to find the right position to insert the new node in a binary tree.

Space Complexity: O(n)
Since we are using the queue to store the tree nodes.

Run Time Testcases

In this case, we are inserting the nodes in binary tree.

 
--- Binary Tree -- 
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal  
6. Preorder Traversal 
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 1
 
Enter data for new node: 89
 
 * Node with data 89 was inserted
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert         
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 1
 
Enter data for new node: 56
 
* Node with data 56 was inserted
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 1
 
Enter data for new node: 45
 
* Node with data 45 was inserted
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 1
 
Enter data for new node: 2
 
* Node with data 2 was inserted
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 1
 
Enter data for new node: 55
 
* Node with data 55 was inserted
 
Do you want to continue? (Y/N) n

Delete a Node from the Binary Tree

To delete the node from the tree requires following the given steps:

Traverse the tree to find the node which has the given key.
Traverse to find the deepest node.
Update the data of the key node to the deepest node and then delete the deepest node.

Example: Delete node 34 in the given tree.

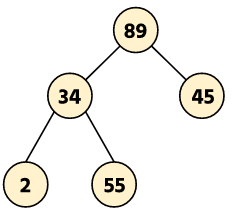
The deepest leftmost node is 55. So replace the deepest node value with the key node.

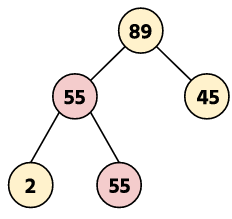
Now delete the deepest node.

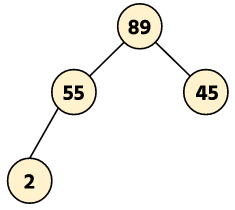
Time Complexity: O(n)
To delete the deepest node we have to traverse the entire tree of size n, where n is the number of nodes in the tree.

Space Complexity: O(n)
Since we are using the queue for the level order traversal. In the worst case, the space depends on the number of nodes in the tree, which is n.

Run Time Testcases

In this case, we are deleting the nodes in binary tree.
Note: The data in the Binary Tree are {89 56 45 2 55}

 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 8
 
Level order Traversal
 
89 56 45 2 55 
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 2
Enter node data: 56
* Node with data 56 was deleted
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 8
 
Level order Traversal
 
89 55 45 2
 
Do you want to continue? (Y/N) n

Searching a Node in a Binary Tree

To search a node with the given key we use the level order traversal. Searching a node in a Binary tree needs to follow the given steps:

Compare the key with each node value and if found the key then return 1 else return -1.

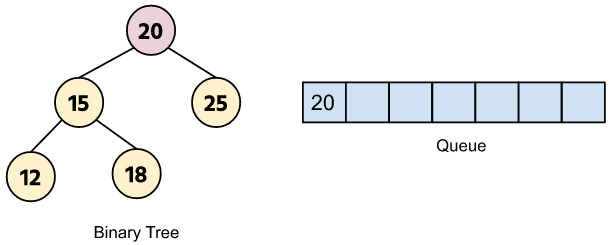
Example: Let’s find the node with data 15 in the given Binary Tree.

Push the root node into the stack and compare it with the key.

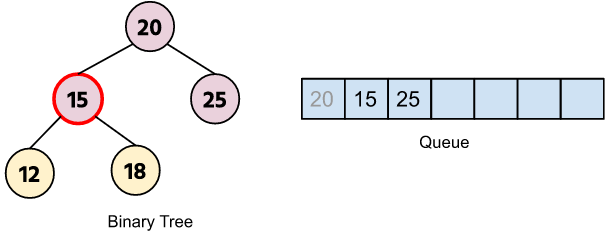
Since, 20 is not equal to 15 so we will push its children and check the data for the other nodes.

The data of the left child of the root node is equal to the key so we have found the key then return 1.

Time Complexity: O(n)
In the worst case, we have to traverse each node. Here n is the number of nodes in the binary tree.

Space Complexity: O(n)
We are storing the nodes in the queue so in the worst case it takes the linear amount of space.

Run Time Testcases

In this case, we are searching the nodes in binary tree.
Note: The data in the Binary Tree are {89 56 45 2 55}

--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 8
 
Level order Traversal
 
89 56 45 2 55 
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 3
Enter node data: 89
Node was found
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 3
Enter node data: 89
Node not found
 
Do you want to continue? (Y/N) n

Traversals of the Binary Tree

Inorder Traversal

In inorder traversal, we have to traverse in the following order:

Traverse to the left to a given node.
print the node data.
Traverse to the right to a given node.

Example: Inorder traversal of the tree is given below.

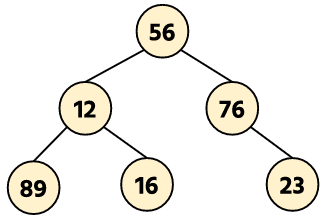
Inorder traversal of the tree: 89, 12, 16, 56, 76, 23

Time Complexity: O(n)
The time complexity of the inorder traversal of a binary tree is O(n). Here, n is the number of nodes. We have to traverse each node in the Binary tree.

Space Complexity: O(h)
The space complexity of the inorder traversal of a binary tree is O(h). Function calling stack requires space of stack.

Run Time Testcases

In this case, we perform an in-order traversal of the binary tree.
Note: The data in the Binary Tree are {89 56 45 2 55}

--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 5
 
Inorder Traversal
 
2 56 55 89 45 
 
Do you want to continue? (Y/N) n

Preorder Traversal

In preorder traversal, we have to traverse in the following order:

Print the node data.
Traverse to the left to a given node.
Traverse to the right to a given node.

Example: Preorder traversal of the binary tree is given below.

Preorder traversal of the tree: 89, 56, 2, 55, 45

Time Complexity: O(n)
The time complexity of the preorder traversal of a binary tree is O(n). Here, n is the number of nodes. We have to traverse each node in the Binary tree.

Space Complexity: O(h)
The space complexity of the preorder traversal of a binary tree is O(h). Function calling stack requires space of stack.

Run Time Testcases

In this case, we perform an preorder traversal of the binary tree.
Note: The data in the Binary Tree are {89 56 45 2 55}

--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 6
 
Preorder Traversal
 
89 56 2 55 45 
 
Do you want to continue? (Y/N) n

Postorder Traversal

In preorder traversal, we have to traverse in the following order:

Traverse to the left to a given node.
Traverse to the right to a given node.
Print the data of the node.

Example: Postorder traversal of the binary tree is given below.

Postorder traversal of the tree: 2, 55, 56, 45, 89

Time Complexity: O(n)
The time complexity of the postorder traversal of a binary tree is O(n). Here, n is the number of nodes. We have to traverse each node in the Binary tree.

Space Complexity: O(h)
The space complexity of the postorder traversal of a binary tree is O(h). Function calling stack requires space of stack.

Run Time Testcases

In this case, we perform an postorder traversal of the binary tree.
Note: The data in the Binary Tree are {89 56 45 2 55}

--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 7
 
Postorder Traversal
 
2 55 56 45 89 
 
Do you want to continue? (Y/N) y
 
--- Binary Tree --
 
1. Insert 
2. Delete
3. Search
4. Height
5. Inorder Traversal
6. Preorder Traversal
7. Postorder Traversal
8. Level order Traversal
9. Exit
 
Enter Your Choice: 4
height of the tree is: 3
 
Do you want to continue? (Y/N) n

To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.

If you find any mistake above, kindly email to [email protected]

« Prev - Hello World Program in C

» Next - C Program to Check Symmetric Matrix

Related Posts:

Recommended Articles: