AVL Tree in C | AVL Tree Program in C

What is an AVL Tree?

The AVL tree in C is a height-balanced binary search tree which means it is also a binary tree that is balanced by the left and right subtree of a node. The tree is said to be balanced when the balance factor of each node is either -1, 0, or +1.

The Balance factor of a tree can be defined as:

Balanced Factor(X) = height(left Subtree (X)) – height(right Subtree(X))

Example of AVL Tree:

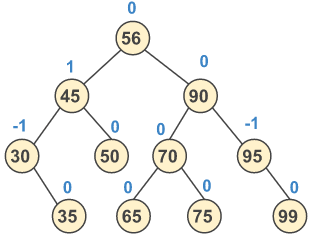
The above binary search tree is satisfying the condition of the balance factor, so it is an AVL tree.

Operations on AVL Tree in C

There are basically three kinds of operations that are performed in the AVL tree:

Insertion of a New Node
Deletion of a Node

Deleting a Node from the Right Subtree
Deleting a Node from the Left Subtree

Searching a Node in AVL Tree

To perform these operations, we have to do the following four kinds of rotations:

LL Rotation (Left Rotation)
RR Rotation (Right Rotation)
LR Rotation (Left Right Rotation)
RL Rotation (Right Left Rotation)

Let’s discuss these operations in detail and understand how these rotations work.

LL Rotation (Left Rotation)

In LL rotation, all the nodes are moved by one position to the left. To understand LL rotation, we have to take into consideration the following insertion operation.

Example: Insert 5, 6, and 9

Note: Join free Sanfoundry classes at Telegram or Youtube

RR Rotation (Right Rotation)

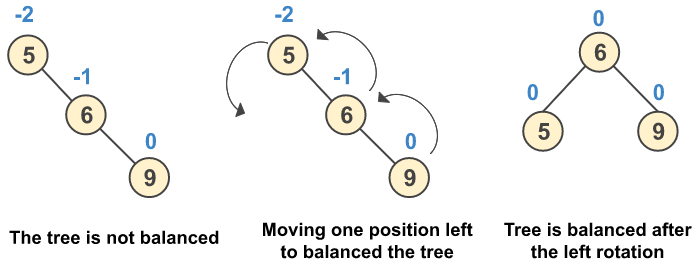
In RR rotation, all the nodes are moved by one position to the right. To understand RR rotation, we have to take into consideration the following insertion operation.

Example: Insert 5, 4, and 3

LR Rotation (Left Right Rotation)

In LR rotation, at the first step, every node moves to the left and then moves one step to the right from the current position. Let’s understand the LR rotation with the given example.

Example: Insert 6, 4, and 5

RL Rotation (Right Left Rotation)

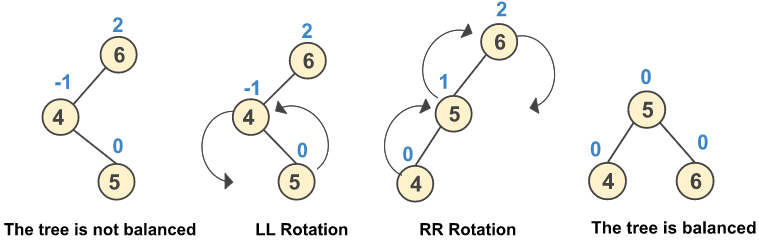
In RL rotation, at the first step, every node moves to the right and then moves one step to the left from the current position. Let’s understand the RL rotation with the given example.

Example: Insert 4, 6, and 5

Problem Description

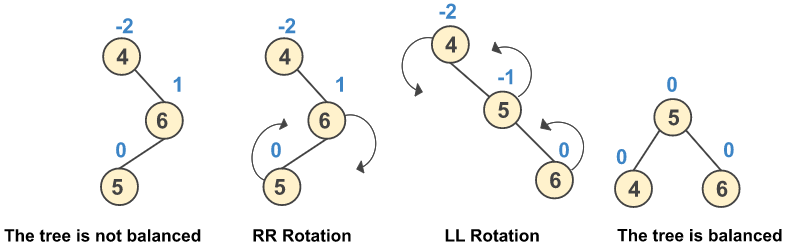
Write a C program to perform the operations of the AVL tree and display its traversals.

Problem Solution

An AVL (Adelson-Velskii and Landis) tree is a self-height balance tree. These trees are binary search trees in which the height of two siblings are not allowed to differ by more than one. We have used the doubly linked list implementation of the AVL tree in which every node contains the address of the left and right children and the data.

Here, we are implementing the main operations of the AVL tree these are given below:

Insert
Delete
Search

Program/Source Code

Here is source code of the C Program to Implement AVL Tree. The C program is successfully compiled and run on a Linux system. The program output is also shown below.

```
/*
```
```
 * AVL Tree Program in C
```
```
 */
```
```
 
```
```
#include<stdio.h>
```
```
#include<stdlib.h>
```
```
 
```
```
// structure of the tree node
```
```
struct node
```
```
{
```
```
    int data;
```
```
    struct node* left;
```
```
    struct node* right;
```
```
    int ht;
```
```
};
```
```
 
```
```
// global initialization of root node
```
```
struct node* root = NULL;
```
```
 
```
```
// function prototyping
```
```
struct node* create(int);
```
```
struct node* insert(struct node*, int);
```
```
struct node* delete(struct node*, int);
```
```
struct node* search(struct node*, int);
```
```
struct node* rotate_left(struct node*);
```

struct node* rotate_right(struct node*);

```
int balance_factor(struct node*);
```
```
int height(struct node*);
```
```
void inorder(struct node*);
```
```
void preorder(struct node*);
```
```
void postorder(struct node*);
```
```
 
```
```
int main()
```
```
{
```
```
    int user_choice, data;
```
```
    char user_continue = 'y';
```
```
    struct node* result = NULL;
```
```
 
```

    while (user_continue == 'y' || user_continue == 'Y')

```
    {
```

        printf("\n\n------- AVL TREE --------\n");

```
        printf("\n1. Insert");
```
```
        printf("\n2. Delete");
```
```
        printf("\n3. Search");
```
```
        printf("\n4. Inorder");
```
```
        printf("\n5. Preorder");
```
```
        printf("\n6. Postorder");
```
```
        printf("\n7. EXIT");
```
```
 
```

        printf("\n\nEnter Your Choice: ");

```
        scanf("%d", &user_choice);
```
```
 
```
```
        switch(user_choice)
```
```
        {
```
```
            case 1:
```

                printf("\nEnter data: ");

```
                scanf("%d", &data);
```

                root = insert(root, data);

```
                break;
```
```
 
```
```
            case 2:
```

                printf("\nEnter data: ");

```
                scanf("%d", &data);
```

                root = delete(root, data);

```
                break;
```
```
 
```
```
            case 3:
```

                printf("\nEnter data: ");

```
                scanf("%d", &data);
```

                result = search(root, data);

```
                if (result == NULL)
```
```
                {
```

                    printf("\nNode not found!");

```
                }
```
```
                else
```
```
                {
```

                    printf("\n Node found");

```
                }
```
```
                break;
```
```
            case 4:
```
```
                inorder(root);
```
```
                break;
```
```
 
```
```
            case 5:
```
```
                preorder(root);
```
```
                break;
```
```
 
```
```
            case 6:
```
```
                postorder(root);
```
```
                break;
```
```
 
```
```
            case 7:
```

                printf("\n\tProgram Terminated\n");

```
                return 1;
```
```
 
```
```
            default:
```

                printf("\n\tInvalid Choice\n");

```
        }
```
```
 
```

        printf("\n\nDo you want to continue? ");

```
        scanf(" %c", &user_continue);
```
```
    }
```
```
 
```
```
    return 0;
```
```
}
```
```
 
```
```
// creates a new tree node
```
```
struct node* create(int data)
```
```
{
```

    struct node* new_node = (struct node*) malloc (sizeof(struct node));

```
 
```
```
    // if a memory error has occurred
```
```
    if (new_node == NULL)
```
```
    {
```

        printf("\nMemory can't be allocated\n");

```
        return NULL;
```
```
    }
```
```
    new_node->data = data;
```
```
    new_node->left = NULL;
```
```
    new_node->right = NULL;
```
```
    return new_node;
```
```
}
```
```
 
```
```
// rotates to the left
```

struct node* rotate_left(struct node* root)

```
{
```

    struct node* right_child = root->right;

```
    root->right = right_child->left;
```
```
    right_child->left = root;
```
```
 
```
```
    // update the heights of the nodes
```
```
    root->ht = height(root);
```

    right_child->ht = height(right_child);

```
 
```

    // return the new node after rotation

```
    return right_child;
```
```
}
```
```
 
```
```
// rotates to the right
```

struct node* rotate_right(struct node* root)

```
{
```

    struct node* left_child = root->left;

```
    root->left = left_child->right;
```
```
    left_child->right = root;
```
```
 
```
```
    // update the heights of the nodes
```
```
    root->ht = height(root);
```

    left_child->ht = height(left_child);

```
 
```

    // return the new node after rotation

```
    return left_child;
```
```
}
```
```
 
```

// calculates the balance factor of a node

```
int balance_factor(struct node* root)
```
```
{
```
```
    int lh, rh;
```
```
    if (root == NULL)
```
```
        return 0;
```
```
    if (root->left == NULL)
```
```
        lh = 0;
```
```
    else
```
```
        lh = 1 + root->left->ht;
```
```
    if (root->right == NULL)
```
```
        rh = 0;
```
```
    else
```
```
        rh = 1 + root->right->ht;
```
```
    return lh - rh;
```
```
}
```
```
 
```
```
// calculate the height of the node
```
```
int height(struct node* root)
```
```
{
```
```
    int lh, rh;
```
```
    if (root == NULL)
```
```
    {
```
```
        return 0;
```
```
    }
```
```
    if (root->left == NULL)
```
```
        lh = 0;
```
```
    else
```
```
        lh = 1 + root->left->ht;
```
```
    if (root->right == NULL)
```
```
        rh = 0;
```
```
    else
```
```
        rh = 1 + root->right->ht;
```
```
 
```
```
    if (lh > rh)
```
```
        return (lh);
```
```
    return (rh);
```
```
}
```
```
 
```
```
// inserts a new node in the AVL tree
```

struct node* insert(struct node* root, int data)

```
{
```
```
    if (root == NULL)
```
```
    {
```

        struct node* new_node = create(data);

```
        if (new_node == NULL)
```
```
        {
```
```
            return NULL;
```
```
        }
```
```
        root = new_node;
```
```
    }
```
```
    else if (data > root->data)
```
```
    {
```

        // insert the new node to the right

        root->right = insert(root->right, data);

```
 
```

        // tree is unbalanced, then rotate it

```
        if (balance_factor(root) == -2)
```
```
        {
```

            if (data > root->right->data)

```
            {
```

                root = rotate_left(root);

```
            }
```
```
            else
```
```
            {
```

                root->right = rotate_right(root->right);

                root = rotate_left(root);

```
            }
```
```
        }
```
```
    }
```
```
    else
```
```
    {
```

        // insert the new node to the left

        root->left = insert(root->left, data);

```
 
```

        // tree is unbalanced, then rotate it

```
        if (balance_factor(root) == 2)
```
```
        {
```

            if (data < root->left->data)

```
            {
```

                root = rotate_right(root);

```
            }
```
```
            else
```
```
            {
```

                root->left = rotate_left(root->left);

                root = rotate_right(root);

```
            }
```
```
        }
```
```
    }
```
```
    // update the heights of the nodes
```
```
    root->ht = height(root);
```
```
    return root;
```
```
}
```
```
 
```
```
// deletes a node from the AVL tree
```

struct node * delete(struct node *root, int x)

```
{
```
```
    struct node * temp = NULL;
```
```
 
```
```
    if (root == NULL)
```
```
    {
```
```
        return NULL;
```
```
    } 
```
```
 
```
```
    if (x > root->data)
```
```
    {
```

        root->right = delete(root->right, x);

```
        if (balance_factor(root) == 2)
```
```
        {
```

            if (balance_factor(root->left) >= 0)

```
            {
```

                root = rotate_right(root);

```
            }
```
```
            else
```
```
            {
```

                root->left = rotate_left(root->left);

                root = rotate_right(root);

```
            }
```
```
        }
```
```
    }
```
```
    else if (x < root->data)
```
```
    {
```

        root->left = delete(root->left, x);

```
        if (balance_factor(root) == -2)
```
```
        {
```

            if (balance_factor(root->right) <= 0)

```
            {
```

                root = rotate_left(root);

```
            }
```
```
            else
```
```
            {
```

                root->right = rotate_right(root->right);

                root = rotate_left(root);

```
            }
```
```
        }
```
```
    }
```
```
    else
```
```
    {
```
```
        if (root->right != NULL)
```
```
        { 
```
```
            temp = root->right;
```
```
            while (temp->left != NULL)
```
```
                temp = temp->left;
```
```
 
```
```
            root->data = temp->data;
```

            root->right = delete(root->right, temp->data);

            if (balance_factor(root) == 2)

```
            {
```

                if (balance_factor(root->left) >= 0)

```
                {
```

                    root = rotate_right(root);

```
                }
```
```
                else
```
```
                {
```

                    root->left = rotate_left(root->left);

                    root = rotate_right(root);

```
                }
```
```
            }
```
```
        }
```
```
        else
```
```
        {
```
```
            return (root->left);
```
```
        }
```
```
    }
```
```
    root->ht = height(root);
```
```
    return (root);
```
```
}
```
```
 
```
```
// search a node in the AVL tree
```

struct node* search(struct node* root, int key)

```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return NULL;
```
```
    }
```
```
 
```
```
    if(root->data == key)
```
```
    {
```
```
        return root;
```
```
    }
```
```
 
```
```
    if(key > root->data)
```
```
    {
```
```
        search(root->right, key);
```
```
    }
```
```
    else
```
```
    {
```
```
        search(root->left, key);
```
```
    } 
```
```
}
```
```
 
```
```
// inorder traversal of the tree
```
```
void inorder(struct node* root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
 
```
```
    inorder(root->left);
```
```
    printf("%d ", root->data);
```
```
    inorder(root->right);
```
```
}
```
```
 
```
```
// preorder traversal of the tree
```
```
void preorder(struct node* root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
 
```
```
    printf("%d ", root->data);
```
```
    preorder(root->left);
```
```
    preorder(root->right);
```
```
}
```
```
 
```
```
// postorder traversal of the tree
```
```
void postorder(struct node* root)
```
```
{
```
```
    if (root == NULL)
```
```
    {
```
```
        return;
```
```
    }
```
```
 
```
```
    postorder(root->left);
```
```
    postorder(root->right);
```
```
    printf("%d ", root->data);
```
```
}
```

Program Explanation

The AVL tree is an extension to the binary search tree in which it is required to balance the height difference between the left and right subtree of a node. We can balance the height of the tree by rotations. Let’s understand the main operations of the AVL Tree with the examples and also discuss their time and space complexities.

Insert a Node in AVL Tree

On Inserting a new node into the AVL Tree it is necessary to maintain the balance factor of the tree. To insert a new node into the AVL tree, we have to follow the given steps:

Insert a new element in the tree with the same binary search tree logic.
Check the balance factor for each node.
If the balanced factor is not -1 or 0 or +1 of any node then do the proper rotations else terminate.

Example: We are constructing the AVL Tree by inserting the following values.

Step 1: Insert a new node 10

Step 2: Insert a new node 15

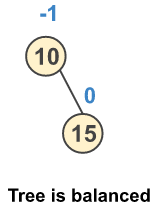
Step 3: Insert a new node 20

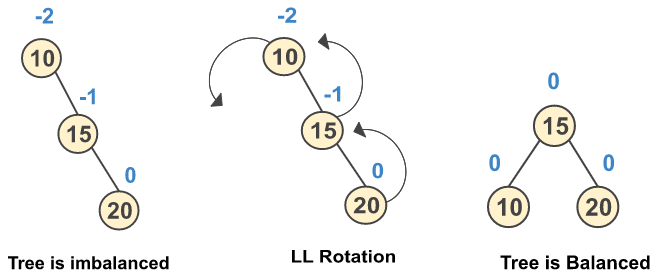
Step 4: Insert a new node 9

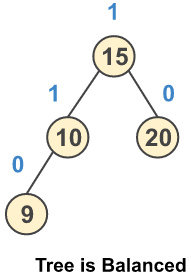
Step 5: Insert a new node 5

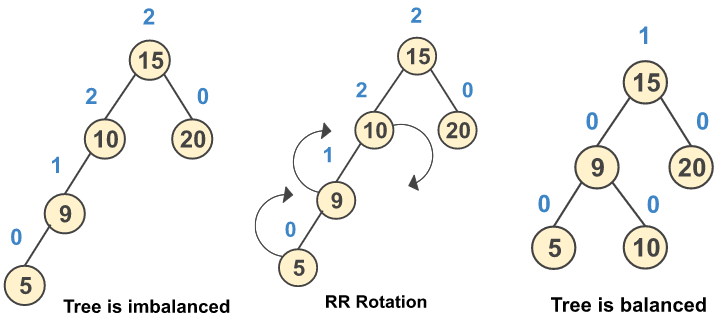
Step 6: Insert a new node 16

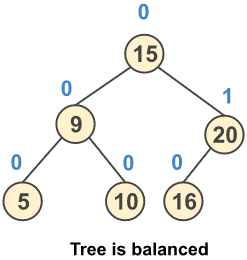
Step 7: Insert a new node 17

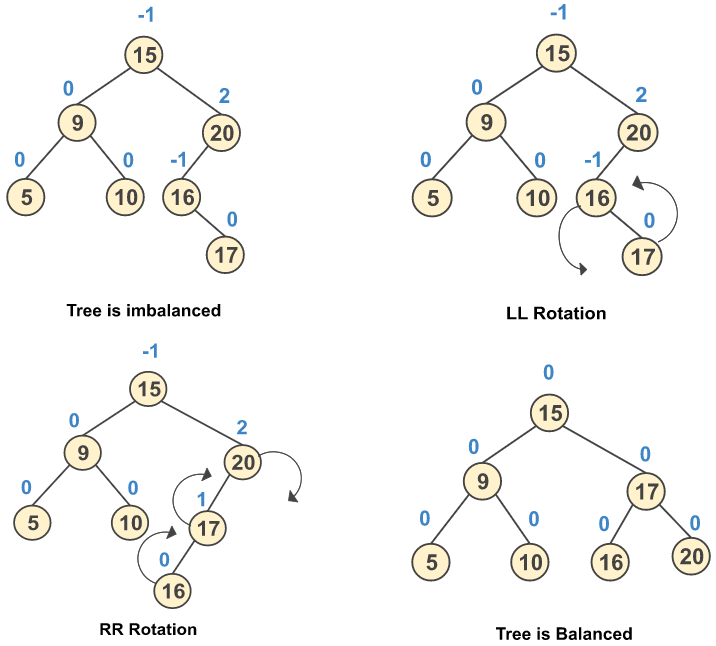
Step 8: Insert a new node 8

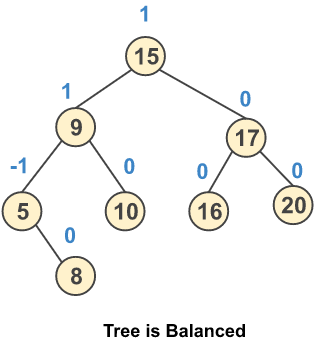
Step 9: Insert a new node 6

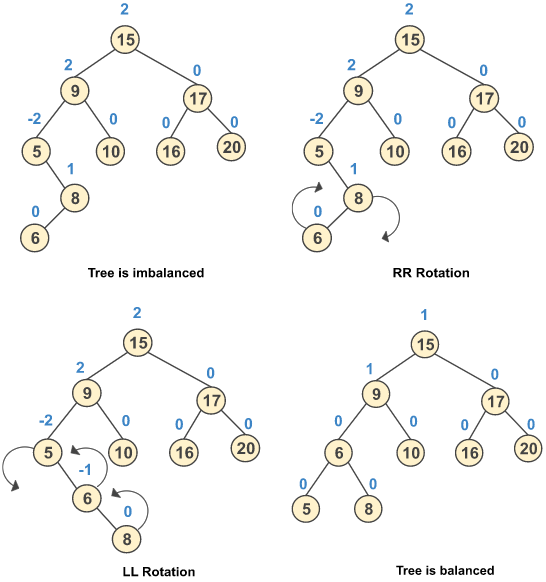
Time Complexity: O(log n)
Time complexity of an AVL tree is O(log n). Inserting any node in the AVL tree takes logarithmic time because each call skips half the tree to determine the correct position to insert a node.

Space Complexity: O(n)
The space complexity of an avl tree is O(n), because the function calling stack eventually exceeds the number of nodes in the tree.

Run Time Testcases

In this case, we are inserting the nodes into AVL tree and finding traversals.

------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 1     
 
Enter data: 34
 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 1     
 
Enter data: 78
 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 1
 
Enter data: 99
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 4
34 78 99 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 5
78 34 99 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 6
34 99 78 
 
Do you want to continue? n

Delete a Node from AVL Tree

Deletion of a node is similar to that of deleting a node in the binary search tree. In AVL Tree, after deleting the node we have to maintain the balanced factor again. We need to follow the given steps to delete a node in AVL Tree:

Search the element in the tree
Delete the node
There are two cases that are possible after deletion

Deleting from the right subtree
Deleting from the left subtree

Case 1: Deleting a Node from the Right Subtree
There are three subcases that are discussed below:

a) Perform LL rotation when after deletion of a node the balance factor of a node changes to +2 and the balance factor of its left child is +1.

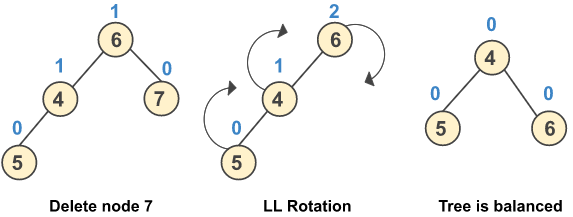
b) Perform LL rotation when after deletion of a node the balance factor of a node changes to +2 and the balance factor of its left child is 0.

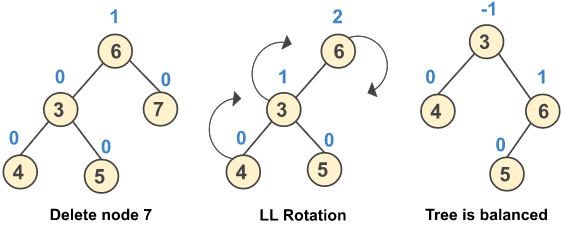
c) Perform LR rotation when after deletion of a node the balance factor of a node changes to +2 and the balance factor of its left child is -1.

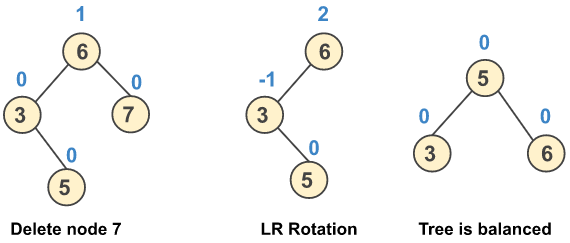
Case 2: Deleting a Node from the Left Subtree
There are three subcases that are discussed below:

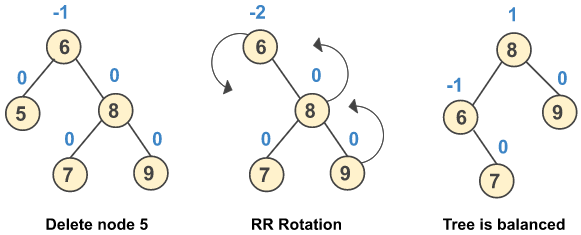
a) Perform RR rotation when after deletion of a node the balance factor of a node changes to -2 and the balance factor of its left child is -1.

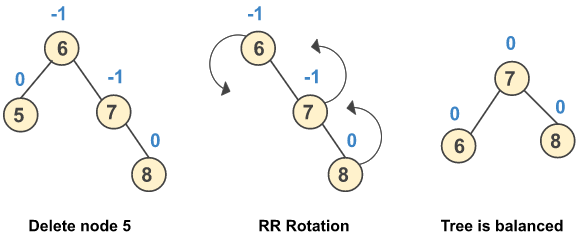
b) Perform RR rotation when after deletion of a node the balance factor of a node changes to -2 and the balance factor of its left child is 0.

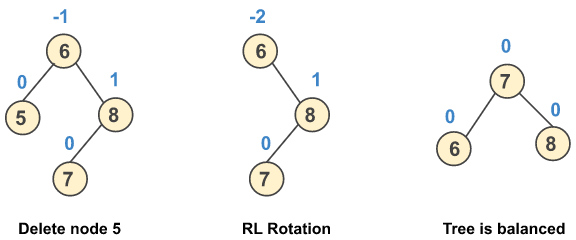
c) Perform RL rotation when after deletion of a node the balance factor of a node changes to -2 and the balance factor of its left child is 1.

Time Complexity: O(log n)
To delete a node from the AVL tree, it takes logarithmic time to find and delete the given node i.e O(log n).

Space Complexity: O(n)
It takes n function calls for deletion and rebuilding the node from the AVL tree.

Run Time Testcases

In this case, we are deleting the nodes from the AVL tree.

------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 1     
Enter data: 34
 
Enter Your Choice: 1     
Enter data: 78
 
Enter Your Choice: 1
Enter data: 99
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 4
34 78 99 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 2
Enter data: 78
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 4
34 99

Searching a Node in AVL Tree

Searching a node in an AVL tree is a similar process that we do in a binary search Tree. Follow the given steps to search a node in AVL Tree.

Start comparing the key with the root node of the tree.
If the key is greater than the node value then move to the right subtree.
If the key is less than the node value then move to the left subtree.
Repeat the process until the key is not found.

Time Complexity: O(log n)
It takes logarithmic time to search any node in the AVL tree.

Space Complexity: O(h)
There are h function calls required to find the node in the AVL tree, where h is the height of the AVL tree.

Run Time Testcases

In this case, we are searching the node in the AVL tree.

------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 1     
Enter data: 34
 
Enter Your Choice: 1     
Enter data: 78
 
Enter Your Choice: 1
Enter data: 99
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 4
34 78 99 
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 3
Enter data: 99
Node found
 
Do you want to continue? y
------- AVL TREE --------
 
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
 
Enter Your Choice: 3
Enter data: 66
Node not found!
 
Do you want to continue? n

To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.

If you find any mistake above, kindly email to [email protected]

« Prev - C Program to Implement Trie

» Next - C Program to Perform Left and Right Rotation on a Binary Search Tree

Related Posts:

Recommended Articles: