This set of Theory of Machines Multiple Choice Questions & Answers (MCQs) focuses on “Single Plate Clutch”.
1. Which of these is not a type of clutch?
a) Single disc
b) Conical
c) Centrifugal
d) Cylindrical
View Answer
Explanation: Single disc, conical and centrifugal are types of clutches. Clutches are used for the transmission of power in shafts and machines which are started and stopped frequently. It is also used to deliver power to the machine which are partially or fully loaded.
2. Identify the clutch.
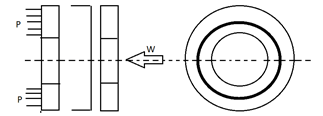
a) Single plate clutch
b) Conical clutch
c) Centrifugal clutch
d) Multi plate clutch
View Answer
Explanation: The given diagram is of a single plate clutch. It consists of a clutch plate whose both sides are faced with Ferrodo (a friction material). It is mounted on the hub which moves along the splines of the shaft which is driven.
3. In a single plate clutch, considering uniform pressure, T = nµWR. What is R equal to?
a) 2(r13 + r23) / 3(r12 + r22)
b) 2(r13 – r23) / 3(r12 – r22)
c) (r1 – r2)/2
d) (r1 + r2)/2
View Answer
Explanation: For uniform pressure theory, T = nµW(2(r13 – r23) / 3(r12 – r22))
Therefore, considering uniform pressure theory in a single plate clutch, T = nµWR where R = 2(r13 – r23) / 3(r12 – r22).
4. In a single plate clutch, considering uniform wear, T = nµWR. What is R equal to?
a) 2(r13 + r23) / 3(r12 + r22)
b) 2(r13 – r23) / 3(r12 – r22)
c) (r1 – r2)/2
d) (r1 + r2)/2
View Answer
Explanation: For uniform wear, T = nµW((r1 + r2)/2)
Therefore, considering uniform pressure theory in a single plate clutch, T = nµWR where R = (r1 + r2)/2.
5. The intensity of pressure is minimum at the outer radius that is r1. True or false?
a) True
b) False
View Answer
Explanation: The intensity of pressure is minimum at the outer radius that is r1. It is given by C/r1. The intensity of pressure is maximum at the inner radius which is r2.
6. In a single plate clutch, the pressure is uniformly distributed. If the outer and inner radii are 100 mm and 70 mm respectively, find the value of R.
a) 76.39 mm
b) 23.48 mm
c) 85.88 mm
d) 34.98 mm
View Answer
Explanation: Considering uniform pressure theory in a single plate clutch, T = nµWR where R = 2(r13 + r23) / 3(r12 + r22)
Thus, here, R = 2(1003 – 703) / 3(1002 – 702) = 85.88 mm.
7. Maximum intensity of pressure is given by ____
a) C/R
b) C/R2
c) C/r2
d) C/r1
View Answer
Explanation: We know that, pmax x r2 = C.
Thus, pmax = C/r2
Similarly, pmin = C/r1
8. When the pressure is uniformly distributed over entire area, then the intensity of pressure is _______________
a) W/ (π(r12 – r22)
b) W/ (π(r12 + r22)
c) W/ (π(r22 – r12))
d) W/ (π(r22 x r12))
View Answer
Explanation: Pressure = Force / Area
Therefore, the intensity of pressure considering uniform pressure is W/ (π(r12 – r22).
9. For uniform wear, the axial thrust W = ______________
a) 2 π C (r2 + r1)
b) 2 π C (r1 – r2)
c) 2 π C (r2 – r1)
d) 2 π C (r1 x r2)
View Answer
Explanation: In uniform wear theory, C = W/(2 π (r1 – r2))
Thus, W = 2 π C (r1 – r2).
10. Find the axial thrust to be provided by the springs if the maximum intensity of pressure in a single plate clutch should not exceed 0.2 N/mm2. The outer and the inner radius is 75 mm and 35 mm. Assume theory of uniform wear.
a) 1792.01 N
b) 1789.21 N
c) 1723.41 N
d) 1759.29 N
View Answer
Explanation: Given: pmax = 0.2 N/mm2, r1 = 75 mm and r2 = 35 mm
Thus, W = 2 π C (r1 – r2) = 2 π C (r1 – r2) = 2 π x pmax x r2 (r1 – r2) = 2 π x 0.2 x 35 (75 – 35) = 1759.29 N.
11. Find the average pressure in a single plate clutch if the axial force is 5 kN. The inside radius and the outer radius is 30 mm and 70 mm respectively. Assume uniform wear.
a) 398 N/mm2
b) 0.398 N/m2
c) 0.398 N/mm2
d) 398 N/m2
View Answer
Explanation: Given: W = 5 kN = 5 x 103 N, r1 = 70 mm and r2 = 30 mm
Average pressure = Total normal force on the surface/ Cross sectional area of those surfaces = W/ (π(r12 – r22)) = 5 x 103/(π(702 – 302)) = 0.398 N/mm2.
12. In a single plate clutch if the axial force is equal to 8 kN, find the minimum and maximum intensity of pressure. The outer radius = 100 mm and inner radius = 65 mm.
a) 0.36 N/mm2, 0.56 N/mm2
b) 0.56 N/mm2, 0.36 N/mm2
c) 0.36 N/m2, 0.56 N/m2
d) 0.56 N/m2, 0.36 N/m2
View Answer
Explanation: Given : W = 8 kN = 8 x 103 N, r1 = 100 mm and r2 = 65 mm
Maximum intensity of pressure = pmin = C/r1
Thus, C = 100 x pmin
W = 2 π C (r1 – r2)
Thus,
C = W/(2 π (r1 – r2)) = 8 x 103/ (2 π (100 – 65))
C = 100 x pmin = 36.378
pmin = 0.36 N/mm2
Maximum intensity of pressure = pmax = C/r2
Thus, C = 65 x pmax
W = 2 π C (r1 – r2)
Thus,
C = W/(2 π (r1 – r2)) = 8 x 103/ (2 π (100 – 65))
C = 65 x pmax = 36.378
pmax = 0.56 N/mm2.
13. A single plate clutch, having n = 2, has outer and inner radii 150 mm and 100 mm respectively. The maximum intensity of pressure at any point is 0.1 N/mm2. If the µ is 0.3, determine the power transmitted by a clutch at a speed 3000 r.p.m.
a) 74031 kW
b) 740.31 kW
c) 74.031 kW
d) 706.95 kW
View Answer
Explanation: Given : n = 2, r1 = 150 mm ; r2 = 100 mm ; p = 0.1 N/mm2 ; µ = 0.3 ; N = 3000 r.p.m. or ω = 2π × 3000/60 = 314.16 rad/s.
Since the intensity of pressure (p) is maximum at the inner radius (r2), considering uniform wear, pmax x r2 = C or C = 0.1 × 100 = 10 N/mm.
Axial thrust, W = 2 π C (r1 – r2) = 2π × 10 (150 – 100) = 3142 N
Mean radius = R = (r1 + r2)/2 = 125 mm = 0.125 m.
We know that torque transmitted,
T = n.µ.W.R = 2 × 0.3 × 3142 × 0.125 = 235.65 N-m
Thus, power transmitted,
P = T.ω = 235.65 × 314.16 = 74031 W = 74.031 kW.
14. A single plate clutch, having n = 2, has outer and inner radii 200 mm and 175 mm respectively. The maximum intensity of pressure at any point is 0.05 N/mm2. If the µ is 0.4 and the power generated by the clutch is equal to 32.384 kW, determine the speed of the clutch.
a) 209.44 r.p.m.
b) 2000 r.p.m.
c) 157.08 r.p.m.
d) 1500 r.p.m.
View Answer
Explanation: Given : n = 2, r1 = 200 mm ; r2 = 175 mm ; p = 0.05 N/mm2 ; µ = 0.4 ; P = 32.384 kW = 32384 W
Since the intensity of pressure (p) is maximum at the inner radius (r2), considering uniform wear, pmax x r2 = C or C = 0.05 × 175 = 8.75 N/mm
Axial thrust, W = 2 π C (r1 – r2) = 2π × 8.75 (200 – 175) = 1374.44 N
Mean radius = R = (r1 + r2)/2 = 187.5 mm = 0.1875 m.
We know that torque transmitted,
T = n.µ.W.R = 2 × 0.4 × 1374.44 × 0.1875 = 206.16 N-m
Thus, power transmitted,
P = T.ω
ω = P/T = 32384/206.16 = 157.08 rad/s
N = ω x 60 / (2 π) = 1500 r.p.m.
15. A single plate clutch, where n = 2, is required to transmit 30 kW at 3000 r.p.m. Determine the outer and inner radii if the coefficient of friction is 0.3, the ratio of radii is 1.5. pmax = 0.1 N/mm2.
a) 0.111 mm, 0.074 mm
b) 111 mm, 74 mm
c) 74 mm, 111 mm
d) 0.074 mm, 0.111 mm
View Answer
Explanation: Given: n = 2 ; P = 30 kW = 30 × 103 W ; N = 3000 r.p.m. or ω = 2π × 3000/60 = 314.2 rad/s ; µ = 0.3 ; r1/r2 = 1.5 ; p = 0.1 N/mm2.
Since the ratio of radii (r1/r2) is 1.5, therefore r1 = 1.5r2
We know that the power transmitted (P), 30 × 103 = T.ω = T × 314.2 ∴ T = 30 × 103/314.2 = 95.48 N-m = 95.48 × 103 N-mm
The intensity of pressure is maximum at inner radius (r2),
pmax x r2 = C or C = 0.1 x r2 N/mm
W = 2 π C (r1 – r2) = 2 π × 0.1 r2 (1.5r2 – r2) = 0.314 (r2)2
Mean radius for uniform wear = R = (r1 + r2)/2 = 1.25 r2
Torque transmitted (T), 95.48 × 103 = n.µ.W.R = 2 × 0.3 × 0.314 (r2)2 × 1.25 r2 = 0.2355 (r2)3
(r2)3 = 95.48 × 103/0.2355 = 405.43 × 103 or r2 = 74 mm
r1 = 1.5 r2 = 1.5 × 74 = 111 mm.
Sanfoundry Global Education & Learning Series – Theory of Machines.
To practice all areas of Theory of Machines, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Mechanical Engineering MCQs
- Check Mechanical Engineering Books
- Apply for Mechanical Engineering Internship
- Check Theory of Machine Books
- Check Agricultural Engineering Books
