This set of Theory of Machines Multiple Choice Questions & Answers (MCQs) focuses on “Path of Contact”.
1. In the given diagram identify the path of contact.
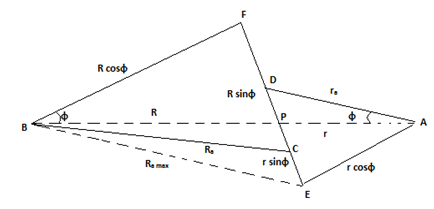
a) CD
b) AB
c) FE
d) BP
View Answer
Explanation: Path of contact is the locus of the point of contact on two mating teeth from the beginning of engagement to the end of it. Thus CD is the path of contact. It is also called as contact length. It is the tangent to both the base circles and passes through the pitch point.
2. The formula to calculate path of contact is ______________________
a) (Ra2 + R2cos2 φ)0.5 + (ra2 + r2cos2 φ)0.5 – (R+r)sin φ
b) (Ra2 – R2cos2 φ)0.5 + (ra2 – r2cos2 φ)0.5 + (R+r)sin φ
c) (Ra2 – R2cos2 φ)0.5 + (ra2 – r2cos2 φ)0.5 – (R+r)sin φ
d) (Ra2 – R2cos2 φ)0.5 + (ra2 – r2cos2 φ)0.5 – (R-r)sin φ
View Answer
Explanation:

From the diagram of two gears in a mesh, we can clearly see that, CD = CP + PD = (CF – PF) + (DE – PE) =(Ra2 – R2cos2 φ)0.5 + (ra2 – r2cos2 φ)0.5 – (R+r)sin φ.
3. The condition which must be fulfilled by two gear tooth profiles to maintain a constant angular velocity ratio between them is called __________________
a) arc of contact
b) path of contact
c) law of gearing
d) interference
View Answer
Explanation: Law of gearing is the condition which must be fulfilled by two gear tooth profiles to maintain a constant angular velocity ratio between them. In order to maintain this constant angular velocity, the common normal of the tooth profiles should always pass through a fixed point on the line of centres, called fixed point.
4. Find the path of contact if r = 20 mm, ra= 25 mm, R = 50 mm, Ra = 55 mm and φ = 20°.
a) 11.836 mm
b) 21.135 mm
c) 69.018 mm
d) 36.046 mm
View Answer
Explanation: Path of contact = (Ra2 – R2cos2 φ)0.5 + (ra2 – r2cos2 φ)0.5 – (R+r)sin φ = 21.135 mm.
5. What is the formula for the path of approach?
a) (Ra2 – R2cos2 φ)0.5 – Rsinφ
b) (Ra2 + R2cos2 φ)0.5 + Rcosφ
c) (Ra2 + R2cos2 φ)0.5 + Rsinφ
d) (Ra2 + R2cos2 φ)0.5 – Rcosφ
View Answer
Explanation: The path of approach is given by the formula (Ra2 + R2cos2 φ)0.5 – Rsinφ; where Ra = The addendum radius of the larger gear, R = The radius of the larger gear and φ is the pressure angle. Path of approach is the portion of path of contact from the beginning of contact to the pitch point. Similarly, the formula for the path of recess is (Ra2 + R2cos2 φ)0.5 – rsinφ.
6. To avoid interference what is the maximum length of the path of approach?
a) Rsinφ
b) rsinφ
c) Rcosφ
d) rcosφ
View Answer
Explanation: The maximum length of the path of approach is equal to rsinφ. Similarly, the maximum length of the path of recess is equal to Rsinφ; where r is the radius of the smaller gear, R is the radius of the larger gear and φ is the pressure angle between these two gears.
7. Two gears in a mesh have 45 teeth each and the module is 5 mm. The pressure angle is given to be φ = 15°. The addendum is equal to 1 module. Find the path of contact.
a) 31.159 mm
b) 48.201 mm
c) 34. 356 mm
d) 42.543 mm
View Answer
Explanation: φ = 15°, t = T = 45 and m = 5 mm. Addendum = 1 module.
R = r = mT/2 = 112.5 mm and Ra = ra = 112.5 + 5 = 117.5 mm
Path of contact = (Ra2 – R2cos2 φ)0.5+ (Ra2 – R2cos2 φ)0.5 – (R+r)sin φ= 31.159 mm.
8. The pressure angle of two gears in a mesh is φ = 20°. The gear ratio is 3 and the number of teeth on the pinion is 20. The module is given to be 8 mm. The addendum is one module. Find the path of contact of these two gears.
a) 21.324 mm
b) 12.543 mm
c) 56.343 mm
d) 39.458 mm
View Answer
Explanation: φ = 20°, t = 20. Hence, T = 20 x 3 = 60. Addendum = 1 module
r = mt/2 = 80 mm, R = mT/2 = 240 mm
ra = r + a = 88 mm, Ra = r + a = 248 mm
Path of contact = (Ra2 – R2cos2 φ)0.5+ (Ra2 – R2cos2 φ)0.5 – (R+r)sin φ = 39.458 mm.
9. The pressure angle of two gears in a mesh is φ = 25°. The number of teeth on the pinion is 25 and the number of teeth on the gear is 70. The module is given to be 10 mm. The addendum is 1.1 times the module. Find the path of approach and path of contact of these gears.
a) 24.421 mm, 22.417 mm
b) 22.417 mm, 24.421 mm
c) 26.407 mm, 20.431 mm
d) 20.431 mm, 26.407 mm
View Answer
Explanation: φ = 25°, t = 25, T = 70, m = 10 mm and addendum = 1.1 module = 11 mm.
r = mt/2 = 125 mm, R = mT/2 = 350 mm
ra = r + a = 136 mm, Ra = R + a = 361 mm
Path of approach = (Ra2 – R2cos2 φ)0.5 – Rsinφ = 24.421 mm
Path of recess = (ra2 – R2cos2 φ)0.5– rsinφ = 22.417 mm.
10. The pressure angle of two gears in a mesh is φ = 15°. The number of teeth on the larger gear is 50. The module is 4 mm. The addendum is equal to be 1.25 module. Find the path of approach of these gears.
a) 39.211 mm
b) 15.287 mm
c) 31.092 mm
d) 21.122 mm
View Answer
Explanation: φ = 15°, T = 50, m = 4 mm and addendum = 1.25 x module = 5 mm
R = mT/2 = 100 mm, Ra = R + a = 105 mm
Path of approach = (Ra2 – R2cos2 φ)0.5 – Rsinφ = 15.287 mm.
11. The pressure angle of two gears in a mesh is φ = 35°. The number of teeth on the pinion is 20. The module is 10 mm and the addendum is 1 module. Find the path of recess of these gears.
a) 34.213 mm
b) 23.328 mm
c) 16.058 mm
d) 32.091 mm
View Answer
Explanation: φ = 35°, t = 20, m = 10 mm and addendum = 1 module = 10 mm.
r = mt/2 = 100 mm and ra = r + a = 110 mm
Path of recess = (ra2 – r2cos2 φ)0.5 – rsinφ= 16.058 mm.
Sanfoundry Global Education & Learning Series – Theory of Machines.
To practice all areas of Theory of Machines, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Check Theory of Machine Books
- Practice Mechanical Engineering MCQs
- Apply for Agricultural Engineering Internship
- Check Agricultural Engineering Books
