This set of Theory of Machines Multiple Choice Questions & Answers (MCQs) focuses on “Conical Clutch”.
1. Identify the given clutch.
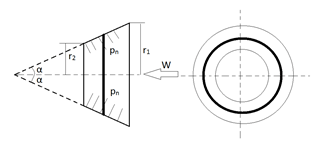
a) Single plate
b) Multi plate
c) Conical
d) Centrifugal
View Answer
Explanation: The given diagram is that of a conical clutch. Conical clutch was used in automobiles earlier but nowadays single plate and multi plate clutches are used instead of it.
2. In a conical clutch, pn = ______________
a) W/(π(r12 – r22))
b) W/(π(r12 + r22))
c) W/(π(r22 – r12))
d) W/(π(r22 x r12))
View Answer
Explanation: Pressure = Force/ Area.
Thus, here, intensity of pressure considering uniform pressure pn is W/(π(r12 – r22)).
3. In a conical clutch, the formula for T is given by ______
a) n.µ.W.R
b) n.µ.W.r1
c) n.µ.W.r2
d) n.µ.W.(r1+r2)
View Answer
Explanation: In a multi plate clutch, the formula for T is given by n.µ.W.R
It is same as that of single plate and multi plate clutch but the value of R is different for conical clutch.
4. In a conical clutch, considering uniform pressure, T = nµWR. What is R equal to?
a) {2(r13 + r23) / 3(r12 + r22)} x cosec α
b) {2(r13 – r23) / 3(r12 – r22)} x cosec α
c) {(r1 – r2)/2} x cosec α
d) {(r1 + r2)/2} x cosec α
View Answer
Explanation: Considering uniform pressure theory in a single plate clutch, T = nµWR where R = {2(r13 – r23) / 3(r12 – r22)} x cosec α
α = the semi cone angle.
5. In a conical clutch, considering uniform wear, T = nµWR. What is R equal to?
a) {2(r13 + r23) / 3(r12 + r22)} x cosec α
b) {2(r13 – r23) / 3(r12 – r22)} x cosec α
c) {(r1 – r2)/2} x cosec α
d) {(r1 + r2)/2} x cosec α
View Answer
Explanation: Considering uniform pressure theory in a single plate clutch, T = nµWR where R = {(r1 + r2)/2} x cosec α.
6. In a conical clutch, what is the axial force required for engaging the clutch (We)?
a) Wn (sin α + µ cos α)
b) Wn (sin α – µ cos α)
c) Wn (µ sin α + cos α)
d) Wn (µ sin α – cos α)
View Answer
Explanation: We = W + µ.Wn cos α = Wn sinα + µ.Wn cosα = Wn (sinα + µcosα). If the semi cone angle of the clutch decreases, the torque produced by the clutch increases which in turn reduces the axial force W.
7. In a conical clutch, what is the axial force required for disengaging the clutch (Wd)?
a) Wn(µcosα + sinα)
b) Wn(µcosα – sinα)
c) Wn(cosα – µsinα)
d) Wn(cosα + µsinα)
View Answer
Explanation: The axial force required for disengaging the clutch i.e. Wd = Wn(µcosα – sinα). The axial force for disengagement is only required if the value of tan α is less than µ.
8. In a conical clutch, the breadth of the contact surface is given by ______
a) (r1 + r2)/sinα
b) (r2-r1)/sinα
c) (r1 – r2)/sinα
d) (r12 + r22)/sinα
View Answer
Explanation: In a conical clutch b sinα = r1-r2
Thus, b = (r1-r2)/sinα
9. In a conical clutch, the mean radius of the bearing surface is 300 mm whereas the breadth is 20 mm. Find the inner and outer radii. The semi cone angle is 30°.
a) 145 mm, 155 mm
b) 140 mm, 160 mm
c) 160 mm, 140 mm
d) 155 mm, 145 mm
View Answer
Explanation: In a conical clutch b sinα = r1 – r2
r1 – r2 = 10 and r1 + r2 = 300
r1 = 155 mm and r2 = 145 mm.
10. If the outer and inner radius of the contact surfaces are 100 mm and 75 mm respectively and the semi cone angle is 22.5°, find the value of the face width required.
a) 89.43 mm
b) 78.94 mm
c) 65.33 mm
d) 23.87 mm
View Answer
Explanation: In a conical clutch b sinα = r1 – r2
b x sin 22.5° = 100 – 75
b = 65.33 mm.
11. A conical friction clutch is used to transmit 75 kW at 1500 r.p.m. The semi cone angle is 20° and the coefficient of friction is 0.3. If the mean diameter of the bearing surface is 500 mm and the intensity of normal pressure is not to exceed 0.1 N/mm2, find the dimensions of the conical bearing surface.
a) 118.07 mm, 131.93 mm
b) 131.93 mm, 118.07 mm
c) 121.72 mm, 128.28 mm
d) 128.28 mm, 121.72 mm
View Answer
Explanation: Given : P = 75 kW = 75 × 103 W ; N = 1500 r.p.m. or ω = 2 π × 1400/60 = 157.08 rad/s ; α = 20° ; µ = 0.3 ; D = 500 mm or R = 250 mm ; pn = 0.1 N/mm2
Power transmitted (P) = 75 × 103 = T.ω = T × 157.08
T = 75× 103/157.08 = 477.4 N-m = 477.4× 103 N-mm
Torque transmitted (T) = 477.4 × 103 = 2 π µ pn.R2.b = 2π × 0.3 × 0.1 (250)2 b = 11780.97 b
b = 40.52 mm
We know that, r1+r2 = 250 and r1-r2 = 40.52 sin 20 = 13.86
Therefore, r1 = 131.93 mm, r2 = 118.07 mm.
12. A conical friction clutch is used to transmit 50 kW at 1000 r.p.m. The semi cone angle is 15° and the coefficient of friction is 0.2. If the mean diameter of the bearing surface is 450 mm and the intensity of normal pressure is not to exceed 0.15 N/mm2, find the axial spring force necessary to engage the clutch.
a) 4796 N
b) 4774 N
c) 4785 N
d) 4742 N
View Answer
Explanation: Given : P = 50 kW = 50 × 103 W ; N = 1000 r.p.m. or ω = 2 π × 1000/60 = 104.72 rad/s ; α = 15° ; µ = 0.2 ; D = 450 mm or R = 225 mm ; pn = 0.15 N/mm2
Power transmitted (P) = 50 × 103 = T.ω = T × 104.72
T = 50× 103/104.72 = 477.4 N-m
477.4 = µ.Wn.R = 0.2 × Wn × 0.225
Wn= 10610.33 N
Axial spring force = We = Wn(sin α + µ cos α) = 10610.33 (sin 15° + 0.2 cos 15°) = 4796 N.
13. A conical friction clutch is used to transmit 40 kW at 1300 r.p.m. The semi cone angle is 12.5° and the coefficient of friction is 0.25. If the mean diameter of the bearing surface is 400 mm and the intensity of normal pressure is not to exceed 0.2 N/mm2, find the axial spring force necessary to disengage the clutch.
a) 154.28 N
b) 121.45 N
c) 201.78 N
d) 162.39 N
View Answer
Explanation: Given : P = 40 kW = 40 × 103 W ; N = 1300 r.p.m. or ω = 2 π × 1300/60 = 136.13 rad/s ; α = 12.5° ; µ = 0.25 ; D = 400 mm or R = 200 mm ; pn = 0.2 N/mm2
Power transmitted (P) = 40 × 103 = T.ω = T × 136.13
T = 40× 103/136.13 = 293.82 N-m
293.82 = µ.Wn.R = 0.25 × Wn × 0.2
Wn = 5876.5 N
Axial spring force = Wd = Wn(µ cos α – sin α) = 5876.5(0.25 cos 12.5°- sin 12.5°) = 162.39 N.
Sanfoundry Global Education & Learning Series – Theory of Machines.
To practice all areas of Theory of Machines, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Agricultural Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Theory of Machine Books
- Check Agricultural Engineering Books
- Check Mechanical Engineering Books
