This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Mass or Inertia Elements”.
1. The inertia property for the particle is
a) Particle mass
b) Particle Volume
c) Particle Density
d) Particle weight
View Answer
Explanation: Particle mass is the only inertia property. The distribution of mass about the mass center is important for a rigid body which is used to describe a property of rigid body called centroid moment of inertia.
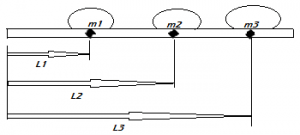
2. Given m1,m2,m3,L1,L2,L3 respectively are 3kg,5kg,6kg,2m,5m,6m. Find the equivalent mass meq
a) 68.25 kg
b) 78.25 kg
c) 88.25 kg
d) 98.25 kg
View Answer
Explanation: This comes under translational mass connected by a rigid bar. The equivalent masses can calculated as meq = m1 + (L2/L1)2 m2 + (L3/L1)2 m3
Substituting values we have meq = 3 +((5/2)2×5)+((6/2)2 ×6))
= 3 + 31.25 + 54
= 88.25kg
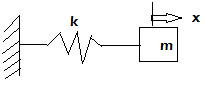
3. The work done by the force is converted into ———–stored in the spring
a) mechanical energy
b) potential energy
c) chemical energy
d) strain energy
View Answer
Explanation: When a force is applied to displace the block from its equilibrium position , the work done by the force is converted into strain energy stored in the spring.
4. If the inertia of the spring has negligible effect on the motion of the block, the system is modeled using————-degree of freedom
a) One
b) Infinite
c) Finite
d) Zero
View Answer
Explanation: If the mass of the spring is much smaller than the mass of the block, its kinetic energy is negligible. In this case inertia of the spring has negligible effect on the motion of the block and the system is modeled using one degree of freedom.
Common data for questions 5 and 6
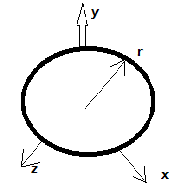
5. Given mass m = 5kg, r = 2m. The moment of inertia through x- axis is Iy= (2/5) × m × r2
a) Yes
b) No
View Answer
Explanation: Given shape of figure is Sphere. Centroidal moment of inertia of three – dimensional body sphere is Ix = (2/5) × m × r2
6. Given mass m = 5kg, r = 2m. The centroidal moment of inertia along z- axis is
a) 5 kg/m2
b) 6 kg/m2
c) 7 kg/m2
d) 8 kg/m2
View Answer
Explanation: Given shape of figure is Sphere. Centroidal moment of inertia of three – dimensional body
sphere is Iz = (2/5) × m × r2
= (2/5) × 5 × 22
= 8 kg/m2
7. For the following Thin disc, given m = 5 kg and r = 4 m
The centroidal moment of inertia along z- axis is
a) 40 kg/m2
b) 20 kg/m2
c) 10 kg/m2
d) 30 kg/m2
View Answer
Explanation: Given shape of figure is Thin disc. Centroidal moment of inertia of three – dimensional body Thin disc is Iz = (¼) × m × r2
= (¼) × 5 × 42
= 20 kg/m2
8. For the following Thin disc, given m = 5 kg and r = 4 m
. The centroidal moment of inertia along x- axis is
a) 40 kg/m2
b) 20 kg/m2
c) 10 kg/m2
d) 30 kg/m2
View Answer
Explanation: Given shape of figure is Thin disc. Centroidal moment of inertia of three – dimensional
Thin disc is Ix = (½) × m × r2
= (½) × 5 × 42
= 40 kg/m2
9. For the following Thin plate, given m = 5 kg, h = 4 m, w = 6 m
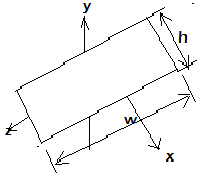. The centroidal moment of inertia along z- axis is
a) 3.333 kg/m2
b) 8.888 kg/m2
c) 7.777 kg/m2
d) 6.666 kg/m2
View Answer
Explanation:Given shape of figure is Thin disc.Centroidal moment of inertia of three – dimensional body
Thin plate is Iz = (1/12) × m × h2
= (1/12) × 5 × 16
= 6.666 kg/m2
10. For the following Thin plate, given m = 5 kg, h = 4 m, w = 6 m
. The centroidal moment of inertia along x- axis is
a) 20 kg/m2
b) 21.66 kg/m2
c) 23.15 kg/m2
d) 22.77 kg/m2
View Answer
Explanation:Given shape of figure is Thin disc. Centroidal moment of inertia of three – dimensional body
Thin plate is Ix = (1/12) × m × ( w2 + h2 )
= (1/12) × 5 × ( 36 + 16 )
= 21.66 kg/m2
Sanfoundry Global Education & Learning Series – Mechanical Vibrations.
To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
