This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Free Vibrations of an Undamped Translational System”.
1. The equation of motion for following system is
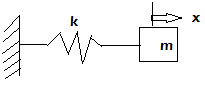
a) m x.. – kx = 0
b) m x.. + kx2 = 0
c) k x.. + mx = 0
d) m x.. + kx = 0
View Answer
Explanation: Newton’s second law states that product of mass and acceleration is the resultant force on the mass. The application of this to the above system yields the equation of motion m x.. + kx = 0 where x.. = d2x/dt2
2. For the following spring- mass system, what is the circular natural frequency ?
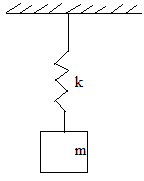
a) (k/m)(1/2)
b) m2/k
c) m/k
d) k/m
View Answer
Explanation: According to the figure, spring mass system is in vertical position, the circular natural frequency for this type of system is ωn = (k/m)(1/2)
3. The undamped natural frequency depends on initial conditions of motion.
a) True
b) False
View Answer
Explanation: The undamped natural frequency depends on mass and stiffness , does not depends on initial conditions or amplitude of motion.
4. The spring constant k can be expressed in terms of m for spring-mass system in vertical position is———-
a) mg/δst
b) 2mg/δst
c) δst/mg
d) δst/2mg
View Answer
Explanation: The spring constant k can be expressed in terms of the massm from ωn(1/2) k = w/δststst(1/2).Thus it is not necessary that we know the spring stiffness and mass.
6. The equation of motion for spring- mass system can also be derived by the conservation of energy principle.
a) Yes
b) No
View Answer
Explanation: It can also derived by the conservation of energy, in this kinetic energy T is stored in the mass and potential energy U in stored in the spring.
7. The natural period of vibration of spring-mass system in vertical position is———-
a) 2п( δst/2g)(1/2)
b) 2п( 2δst/g)(1/2)
c) 2п( δst/g)(1/2)
d) п( δst/g)(1/2)
View Answer
Explanation: The natural period is given by Tn = 1/fn
The natural frequency in cycles per second is given by fn = 1/2п (g/δst )(1/2)
Tn = 1/fn = 2п( δst(1/2)
8. Given spring constant of the hoisting system is keq2d2)/( Πb2d2 + lat3) ). 9. According to the conservation of energy principle , relation between kinetic energy and potential energy is—- 10. The equation of motion for simple spring-mass system is m x.. + kx = 0 . If the gravity effects are induced , the equation is———– Sanfoundry Global Education & Learning Series – Mechanical Vibrations. To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
Find the natural frequency of vibration in vertical direction of hoisting system
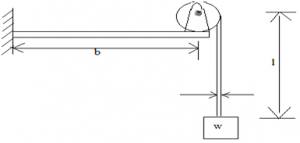
a) [ ( Eg/4w) × ×( (Πat2d
b) [ ( Eg/4w) – ( (Πat2d
c) [ ( Eg/4w) + ( (Πat2d
d) [ ( Eg/4w) × ( (Πat2d
View Answer
Explanation: The natural frequency of vibration in the vertical direction of hoisting system is
ωn = (keq/m)1/2 = ωn = (keqg/w)(1/2) = [ ( Eg/4w) × ( (Πat2d
a) summation of kinetic energy and potential energy is constant
b) both are equal
c) difference between kinetic energy and potential energy is zero
d) summation of kinetic energy and potential energy is zero
View Answer
Explanation: We can derive the equation of motion using conservation of energy principal. The kinetic energy T is stored in the mass and potential energy U is stored in the spring. T + U = constant.
a) x(t) = x(0) sin ωn t + (x. (0)/ ωn ) sin ωn t
b) x(t) = x(0) cos ωn t + (x. (0)/ ωn ) sin ωn t
c) x(t) = x(0) cos ωn t + (x. (0)/ ωn ) cos ωn t
d) x(t) = x(0) cos ωn t – (x. (0)/ ωn ) sin ωn t
View Answer
Explanation: x(t) = x(0) cos ωn t + (x. (0)/ ωn ) sin ωn t, where x(0) is the initial displacement from the equilibrium position and x. (0) is the initial velocity.
