This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Harmonic Analysis”.
1. Who developed a periodic motion in terms of sines and cosines ?
a) C .V Raman
b) Aristotle
c) J. Fourier
d) Newton
View Answer
Explanation: With the help of mathematical series known as Fourier Series, the vibration results obtained experimentally can be analyzed analytically.
2. If s(t) is a periodic function with T, The Fourier series can be written as———
a) (a0/2) + ∑ (an cos nɷt – bn sin nɷt )
b) (a0/2) – ∑ (an cos nɷt – bnsin nɷt )
c) (a0/2) – ∑ (an cos nɷt + bnsin nɷt )
d) (a0/2) + ∑ (an cos nɷt + bnsin nɷt )
View Answer
Explanation: The Fourier series can be written as
s(t) = (a0/2) + a1 cos ɷt + a2 cos 2ɷt + a3 cos 3ɷt +……+ b1 sinɷt + b2 sin 2ɷt + b3 sin 3ɷt +….
= (a0/2) + ∑ (an cos nɷt + bn sin nɷt ) , where a1,a2…,b1,b2…are constant coefficients.
Common data for questions
The Fourier series of periodic function s(t) is (a0/2) + ∑ (an cos nɷt + bn sin nɷt ) .
3. Find an
a) (ɷ/Π) ʃ0 2Π/ɷ s(t) sin (nɷt) dt
b) (ɷ/2Π) ʃ0 2Π/ɷ s(t) cos (nɷt) dt
c) (2ɷ/Π) ʃ0 2Π/ɷ s(t) cos (nɷt) dt
d) (ɷ/Π) ʃ0 2Π/ɷ s(t) cos (nɷt) dt
View Answer
Explanation: s(t) = (a0/2) + ∑ (an cos nɷt + bn sin nɷt ) —-> (1)
an is obtained by multiplying both sides of equation (1) with cos ɷnt and integrating over an interval of time T= 2Π/ɷ.
an = (ɷ/Π) ʃ0 2Π/ɷ s(t) cos (nɷt) dt
4. Find bn
a) (ɷ/Π) ʃ0 2Π/ɷ s(t) cos (nɷt) dt
b) (ɷ/2Π) ʃ0 2Π/ɷ s(t) sin (nɷt) dt
c) (ɷ/Π) ʃ0 2Π/ɷ s(t) sin (nɷt) dt
d) (2ɷ/Π) ʃ0 2Π/ɷ s(t) sin (nɷt) dt
View Answer
Explanation: s(t) = (a0/2) + ∑ (an cos nɷt + bn sin nɷt ) —-> (1)
bn is obtained by multiplying both sides of equation (1) with sin ɷnt and integrating over an interval of time T= 2Π/ɷ.
bn = (ɷ/Π) ʃ0 2Π/ɷ s(t) sin (nɷt) dt
5. Find a0
a) a0 = ɷ/ Π ʃ0 Π/ɷ s(t) dt.
b) a0 = ɷ/ Π ʃ0 2Π/ɷ s(t) dt.
c) a0 = 2ɷ/ Π ʃ0 2Π/ɷ s(t) dt.
d) a0 = ɷ/ 2Π ʃ0 2Π/ɷ s(t) dt.
View Answer
Explanation: s(t) = (a0/2) + ∑ (an cos nɷt + bn sin nɷt ) —-> (1)
a0 is obtained by Integrating both sides of equation (1)
a0 = ɷ/ Π ʃ0 2Π/ɷ s(t) dt.
6. Any periodic motion can be written as sum of harmonic functions
a) Yes
b) No
View Answer
Explanation: s(t) is a periodic function with period T, its Fourier series representation is given by s(t) = (a0/2) + ∑ (an cos nɷt + bn sin nɷt ).
The physical representation of above equation is that any periodic motion can be represented as a sum of harmonic functions.
7. Which of the following term is first Harmonic ?
a) a1 cos ɷt + b1 sin ɷt
b) a2 cos ɷt + b1 sin ɷt
c) a1 cos ɷt + b2 sin ɷt
d) a1 cos ɷt – b1 sin ɷt
View Answer
Explanation: s(t) = (a0/2) + ∑ (an cos nɷt + bn sin n t )
if above equation, the term (a1 cos ɷt + b1 sin ɷt ) is fundamental or first Harmonic and the term (a2 cos 2ɷt + b2 sin 2ɷt ) is called second Harmonic and so on.
8. The following diagram is—-
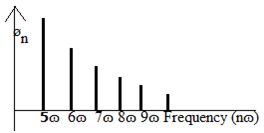
a) Constant coefficient Diagram
b) Amplitude Diagram
c) Frequency Diagram
d) Frequency spectral Diagram
View Answer
Explanation: Harmonics can be plotted as vertical lines on a diagram of amplitude ( an and bn or cn and øn) versus frequency called frequency spectral Diagram.
9. The Fourier series expansion of even function contains only—–terms
a) cosine
b) sine
c) sec
d) tan
View Answer
Explanation: An even function satisfies the relation x(-t) = x(t). In this case the Fourier series of x(t) contains only cosine terms.
x(t) = (a0/2) + ∑ ∞(n=1) an cos nɷt
10. The Fourier series expansion of odd function contains only—–terms
a) cosine
b) sine
c) sec
d) tan
View Answer
Explanation: An odd function satisfies the relation x(-t) = -x(t). In this case the Fourier series of x(t) contains only sine terms.
x(t) = ∑ ∞(n=1) bn sin nɷt
Sanfoundry Global Education & Learning Series – Mechanical Vibrations.
To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
