This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Free Vibrations with Viscous Damping”.
1. Damping resistance due to sliding of one layer of fluid one above the other is called ___________
a) Coulomb damping
b) Dry friction damping
c) Viscous damping
d) Semi-viscous damping
View Answer
Explanation: Since damping involves dissipation of energy, mere presence of a damper in a vibration system makes it non conservative. Viscous damping occurs due to sliding of one layer of fluid over another.
2. Mathematical expression of Newton’s Law of Viscous damping is (symbols have their usual meanings) ___________
a) τ = μ (\(\frac{dv}{dy}\))
b) μ = τ (\(\frac{dv}{dy}\))
c) μ = τ (\(\frac{dy}{dv}\))
d) τ = μ (\(\frac{dy}{dv}\))
View Answer
Explanation: For low rate of shear stress, Newton’s law can be assumed to apply which implies shear stress is directly proportional to the rate of shear strain.
3. Assuming linear velocity gradient, if v is the velocity of one plate w.r.t the other, the force required to move one plate of area A is given by (μ=coefficient of absolute viscosity) ___________
a) F = μA (\(\frac{v}{t}\))
b) F = 2μA (\(\frac{v}{t}\))
c) F = μA (\(\frac{v}{t}\))/2
d) F = A(\(\frac{v}{t}\))
View Answer
Explanation: It follows from the Newton’s law of viscosity; Shear stress is directly proportional to the rate of shear strain. Mathematically, τ = μ (\(\frac{v}{t}\))
Again, τ = \(\frac{F}{A} \) So, replacing the value ofτ, we have F = μA (\(\frac{v}{t}\))
4. What is the differential equation of a damped free vibration model? ẋ And \(\ddot{x}\) are the first and second derivative for x, c is the damping co-efficient and k is the spring constant.
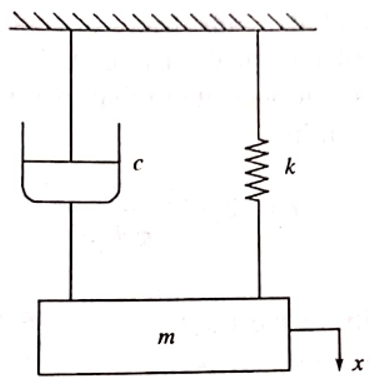
a) mẋ+ c\(\ddot{x}\) = 0
b) m\(\ddot{x}\)+ cx + k\(\ddot{x}\) = 0
c) mx + c\(\ddot{x}\)+ k = 0
d) m\(\ddot{x}\)+ cẋ + kx = 0
View Answer
Explanation: Considering the block diagram and applying Newton’s Law of motion we have:
Rate of change of momentum = ∑Fx
m\(\ddot{x}\)+ cẋ + kx = 0
5. What is the expression for critical damping co-efficient (Cc)? Where, k = spring constant, m = mass.
a) Cc = 2mk
b) Cc = ½ mk
c) Cc = 2\(\sqrt{mk} \)
d) Cc = \(\sqrt{2mk} \)
View Answer
Explanation: By definition, (\(\frac{C_c}{2m}\))2 – \(\frac{k}{m}\) = 0
Cc = \(\sqrt{4m^2(\frac{k}{m})}\) = 2\(\sqrt{mk} \)
6. What is the expression for critical damping co-efficient (Cc) in terms of angular velocity for natural vibration (ωn)?
a) Cc = mωn
b) Cc = mω
c) Cc = m2 ωn
d) Cc = 2m2 ωn
View Answer
Explanation: By definition, (\(\frac{C_c}{2m}\))2 – \(\frac{k}{m}\) = 0
Cc = \(\sqrt{4m^2(\frac{k}{m})}\) = 2 \(\sqrt{mk} \)
Now, since k/m = ωn2 it follows that Cc= 2mωn
7. Damping factor is the ratio of ___________
a) Actual damping co-efficient (c) of the system to the critical damping co-efficient (Cc )
b) Angular velocity of natural vibration (ωn) to actual damping co-efficient (c)
c) Critical damping co-efficient (Cc) to angular velocity of natural vibration (ωn)
d) Angular velocity of natural vibration (ωn) to critical damping co-efficient (Cc)
View Answer
Explanation: When a vibrating system is damped, energy gets continually dissipated. The amplitude of vibration decreases regularly and the system finally comes to rest. Damping factor (ζ) is the ratio of Actual damping co-efficient (c) of the system to the critical damping co-efficient(Cc).
8. What is the condition for over-damped system?
a) Damping factor (ζ) >1
b) Damping factor (ζ) <1
c) Damping factor (ζ) = 1
d) Damping factor (ζ) = 0
View Answer
Explanation: For a system to be over-damped the Damping factor (ζ) should be greater than 1. During over-damping the mass always remains on either on the right hand side or on the left hand side of the mean equilibrium position. So the motion is aperiodic motion.
9. What is the condition for Critically-damped system?
a) Damping factor (ζ) >1
b) Damping factor (ζ) <1
c) Damping factor (ζ) = 1
d) Damping factor (ζ) = 0
View Answer
Explanation: For a system to be critically-damped the Damping factor (ζ) should be equal to 1. Critically damping is a case of aperiodic motion, that is, the mass always remains on either on the right hand side or on the left hand side of the mean equilibrium position. It should be noted that critically damped systems require minimum time to come back to the mean position.
10. Find the value of angular velocity (rad/s) of damped vibration when angular velocity of natural vibration is 30 rad/s and the damping factor is 0.3.
a) 30.21
b) 28.61
c) 30
d) 42.21
View Answer
Explanation: By formula we have, ωd= ωn×\( \sqrt{1-ζ^2} \)
Now replacing the values of angular velocity of natural vibration (ωn) as 30 rad/s and the damping factor as 0.3 in the above formula, we have ωd=28.61 rad/s.
Sanfoundry Global Education & Learning Series – Mechanical Vibrations.
To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
