Mechanical Vibrations Questions and Answers – Free Vibration of Single Degree of Freedom Systems

This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Free Vibration of Single Degree of Freedom Systems”.

1. Free Vibrations occur in the absence of an external excitation
a) Yes
b) No
View Answer

2. When the block is drawn from its equilibrium position, a potential energy developed in the—-

a) Spring
b) Block
c) Spring is kx²
d) Block is kx2/²
View Answer

3.The differential equation governing free vibrations of a linear system are derived in the form——
a) m_eq x.. + c_eq x. + k_eq x = 0
b) c_eq x.. + m_eq x. + k_eq x = 0
c) m_eq x.. – c_eq x. + k_eq x = 0
d) m_eq x.. + k_eq x. + c_eq x = 0
View Answer

4. Free Vibrations of a Single Degree of Freedom system are described by a ——————-
a) Homogenous First order differential equation
b) Homogenous Second order ordinary differential equation
c) Cartesian equation
d) First order differential equation
View Answer

5. Free Vibrations are the result of a kinetic energy imparted to the system
a) True
b) False
View Answer

Common data questions from 6 to 8

The differential equation governing free vibrations of a linear system are derived in the form
m_eq x.. + c_eq x. + k_eq x = 0

6. The Second derivative term is due to—–
a) External forces
b) Velocity
c) Inertia Forces
d) Displacement
View Answer

7. The first derivative term is due to ——-
a) Velocity
b) Viscous damping
c) Elastic forces
d) Displacement
View Answer

8. The Zeroth derivative term is due to
a) Velocity
b) Viscous damping
c) Elastic forces
d) Displacement
View Answer

9. The differential equation governing free vibrations of a linear system are derived in the parameters damping ratio, natural frequency is———–
a) x.. – 2 ζ ωn x. – ωn² x = 0
b) x.. + 2 ζ ωn x. – ωn² x = 0
c) x.. – 2 ζ ωn x. + ωn² x = 0
d) x.. + 2 ζ ωn x. + ωn² x = 0
View Answer

Common data questions from 10 to 12
The differential equation governing free vibrations of a linear system are derived in the form
m_eqx.. + c_eq x. + k_eq x = 0

10. If the energy method is used to derive the differential equation, the Second derivative term is due to—–
a) External forces
b) Kinetic Energy
c) Inertia Forces
d) Displacement
View Answer

11. The first derivative term is due to ——-
a) Viscous friction forces
b) Viscous damping
c) Elastic forces
d) Displacement
View Answer

12. The Zeroth derivative term is due to
a) Potential Energy
b) Viscous damping
c) Elastic forces
d) Displacement
View Answer

Common data for question 13 & 14

The differential equation governing the single degree of freedom system is 5x.. + 4 x. + 7 x = 0

13. Find the natural frequency of motion
a) 3.183
b) 2.183
c) 1.183
d) 0.183
View Answer

The natural frequency of motion is given by ωn = √ ( keq/meq)
Substituting the values, we have  ωn  = √(7/5)
                                      = 1.183 rad/s

14. Find the damping ratio
a) 0.008
b) 0.338
c) 0.118
d) 0.228
View Answer

The damping ratio is given by ζ  = ceq / ( 2 √(k<sub>eq</sub>m<sub>eq</sub>) )
Substituting the values, we have , ζ  = 4 / ( 2 √ (7×5))
                                      = 0.338

15. The differential equation governing the angular oscillation of the compound pendulum is

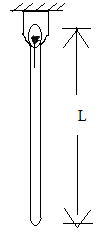
a) m (L²/3) ӫ – mg (L/2) sin ө
b) m (L²/3) ӫ + mg (L2/2) sin ө
c) m (L/3) ӫ + mg (L/2) sin ө
d) m (L²/3) ӫ + mg (L/2) sin ө
View Answer

Sanfoundry Global Education & Learning Series – Mechanical Vibrations.

To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]