This set of Mechanical Vibrations Multiple Choice Questions & Answers (MCQs) focuses on “Free Vibration of Undamped Torsional Systems”.
1. If the rigid body oscillates about a specific reference axis, the resulting motion is called Torsional Vibration.
a) Yes
b) No
View Answer
Explanation: In torsional systems, the rigid body oscillates about a specific axis. The displacement of the body is measured in terms of an angular coordinate.
Common data for questions 2 to 8
Given diagram is the Torsional vibration of a disc with polar moment of inertia J0 , angle of twist of shaft Ɵ , D is the diameter of the disc and d is the diameter of the shaft.
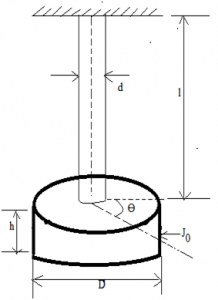
2. The torsional spring constant is
a) ΠGd/32l
b) ΠGd4/32
c) 2ΠGd4/32l
d) ΠGd4/32l
View Answer
Explanation: If the disc is displaced by Ɵ from its equilibrium position, the shaft produces a restoring torque of magnitude Mt. Thus the shaft acts as a torsional spring with a torsional spring constant kt = Mt/Ɵ = GJ/l = Πgd4/32l
3. The equation of motion by applying newton’s second law of motion is —–
a) J0 Ɵ .. – kt Ɵ = 0
b) J0 Ɵ .. + Ɵ = 0
c) J0 .. + kt Ɵ = 0
d) J0Ɵ .. + kt Ɵ = 0
View Answer
Explanation: The equation of the angular motion of the disc about its axis can be derived by using Newton’s second law( mass × acceleration = resultant force) or the principle of conservation of energy.
The equation of motion for given system is J0 Ɵ .. + kt Ɵ = 0
4. The natural frequency of the torsional system is ————–
a) ( kt/ J0 )1/2
b) ( kt/ J0 )
c) ( kt/ J0 )3/4
d) ( 2kt/ J0 )1/2
View Answer
Explanation: The equation of motion for given system is J0 Ɵ .. + kt Ɵ = 0 , where J0 is polar moment of inertia and kt is torsional spring constant. The natural frequency of the torsional system is given by ωn = ( kt/J0 )1/2
5. The frequency of vibration in cycles per second is——–
a) (1/Π) × ( kt// J0 )1/2
b) (1/2Π) × ( kkt// J0 )3/4
c) (1/2Π) × ( kkt// J0 )1/2
d) (1/2Π) × ( kkt// J0 )
View Answer
Explanation: The equation of motion for given system is J0 Ɵ .. + kt Ɵ = 0 , where J0 is polar moment of inertia and kt is torsional spring constant. The frequency of vibration in cycles per second is given by fn = (1/2Π) × ( kt// J0 )1/2
6. The period of vibration is ————
a) 2Π ×( J0 /kt )2
b) 2Π ×( J0 /kt )1/2
c) 2Π ×( J0 /kt )
d) Π ×( J0 /kt )1/2
View Answer
Explanation: The equation of motion for given system is J0 Ɵ .. + kt Ɵ = 0 , where J0 is polar moment of inertia and kt is torsional spring constant. The period of vibration is given by Tn =1/fn
Tn = 2Π ×( J0 /kt )1/2
7. The polar moment of inertia of a disc is given by
a) WD/8g
b) WD2/8g
c) hΠ D4 /t/
d) ρΠ D4 /t/
View Answer
Explanation: The polar moment of inertia of a disc is given by J0 = ρhΠ D4 / 32 = WD4/8g, where ρ is the mass density, D is the diameter, h is the thickness and W is the weight of the disc.
8. The Torsional spring-inertia system shown in given figure is referred to as a —————-
a) Simple Pendulum
b) Torsional pendulum
c) Simple Spring-mass system
d) Twisted Pendulum
View Answer
Explanation: It is referred to as a torsional pendulum. A mechanical rock is one of the important applications of a torsional pendulum.
9. In torsional vibration problem, the restoring moment may be due to the————
a) balanced moment of couple
b) balanced moment of velocity
c) balanced moment of force
d) torsion of an elastic member
View Answer
Explanation: The restoring moment in torsional vibration problem may be due to the unbalanced moment of force or couple or to the torsion of an elastic member.
10. In an automobile , the center of percussion of the vehicle is located near the rear axle. The passenger will not feel any reaction if the front wheels strike a bump.
a) Yes
b) No
View Answer
Explanation: It is desirable to have the center of oscillation of the vehicle and the center of percussion at two different axles. If the front wheels strike a bump and the center of percussion of the vehicle is located near the rear axle, the passenger will not feel any reaction.
Sanfoundry Global Education & Learning Series – Mechanical Vibrations.
To practice all areas of Mechanical Vibrations, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
