This set of Discrete Mathematics Multiple Choice Questions & Answers (MCQs) focuses on “Bipartite Graphs”.
1. The maximum number of edges in a bipartite graph on 14 vertices is ___________
a) 56
b) 14
c) 49
d) 87
View Answer
Explanation: Maximum number of edges occur in a complete bipartite graph when every vertex has an edge to every opposite vertex in the graph. Number of edges in a complete bipartite graph is a*b, where a and b are no. of vertices on each side. This quantity is maximum when a = b i.e. when there are 7 vertices on each side. So answer is 7 * 7 = 49.
2. In a ______ the degree of each and every vertex is equal.
a) regular graph
b) point graph
c) star graph
d) euler graph
View Answer
Explanation: A regular graph has the same degree in each of its vertices. In a regular bipartite graph, if the common degree of each vertices is 1, the two parts are of the same size.
3. The time complexity to test whether a graph is bipartite or not is said to be _______ using depth first search.
a) O(n3)
b) linear time
c) O(1)
d) O(nlogn)
View Answer
Explanation: It is possible to test whether a graph is bipartite, and to return either a two-coloring (if it is bipartite) or an odd cycle (if it is not) in linear time i.e, O(n) using depth first search. In case of the intersection of n line segments or other simple shapes in the Euclidean graph, it is possible to test whether the graph is bipartite and it will return either a two-coloring or an odd cycle in time O(nlogn), even though the graph itself has up to O(n2) edges.
4. The partition V = V1 ∪ V2 in a bipartite graph G1 is called ________
a) bipartition of G1
b) 2-vertex set of G1
c) sub bipartite graphs
d) disjoint vertex set
View Answer
Explanation: A graph G1(V, E) is called bipartite if its vertex set V(G) can be decomposed into two non-empty disjoint subsets V1(G1) and V2(G1) in such a way that each edge e ∈ E(G) has its one end joint in V1(G1) and other endpoint in V2(G1). The partition V = V1 ∪ V2 in a bipartite graph G1 is called bipartition of G1.
5. What is the maximum number of edges in a bipartite graph on 14 vertices?
a) 78
b) 15
c) 214
d) 49
View Answer
Explanation: By definition, the maximum possible number of edges in a bipartite graph on ‘n’ vertices = (1/4) x n2.
Substituting n = 14, we get maximum number of edges in a bipartite graph on 14 vertices,= (1/4) x (14)2
= (1/4) x 14 x 14
= 49
∴ Maximum number of edges in a bipartite graph on 14 vertices = 49.
6. In a complete bipartite graph, the intersection of two sub graphs is ______
a) 1
b) null
c) 210
d) 412
View Answer
Explanation: In a complete Bipartite graph, there must exist a partition say, V(G)=X∪Y and X∩Y=∅, that means all edges share a vertex from both set X and Y.
7. Bipartite graphs are used in ________
a) modern coding theory
b) colouring graphs
c) neural networks
d) chemical bonds
View Answer
Explanation: All types of cyclic graphs are examples of cyclic graphs. A cyclic graph is considered bipartite if all the cycles involved are of even length. Bipartite graphs are widely used in modern coding theory apart from being used in modeling relationships.
8. All closed walks are of ______ length in a bipartite graph.
a) infinite
b) even
c) odd
d) odd prime
View Answer
Explanation: In a bipartite graph G all closed walks must be of even length as well as all cycles in G are of even length. Then only the graph is considered a bipartite graph.
9. Every complete bipartite graph must not be _______
a) planar graph
b) line graph
c) complete graph
d) subgraph
View Answer
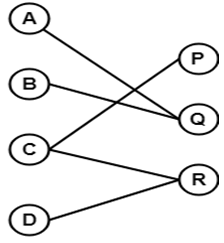
Explanation: The below bipartite graph is not a complete graph as there is no edge between A-B, B-C, C-D, C-Q, P-Q, Q-R, Q-D and so it is not a complete graph.
10. The spectrum of a graph is _______ if and only if it is _______ graph.
a) symmetry, bipartite
b) transitive, bipartite
c) cyclic, Euler
d) reflexive, planar
View Answer
Explanation: A graph is bipartite if and only if it does not contain an odd cycle. The spectrum of a graph is symmetric if and only if it is a bipartite graph. These are the characteristics of the graph.
Sanfoundry Global Education & Learning Series – Discrete Mathematics.
To practice all areas of Discrete Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check BCA Books
- Practice BCA MCQs
- Apply for BCA Internship
- Practice Computer Science MCQs
- Apply for Computer Science Internship
