C++ Program to Check whether a Given Graph is Bipartite or not

This is a C++ Program to Check if a Given Graph is Bipartite.

The problem takes a graph as input and checks whether it is Bipartite or not.

Bipartite Graph is a graph in which the set of vertices can be divided into two sets such that all vertex should be present in either set 1 or set 2 but not both, and there should no edge between vertices belonging to same set.

Example:

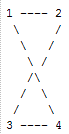
Set 1 = { 1, 3} and Set 2 = {2,4}, and hence the given graph is bipartite.

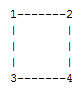
The above graph is not bipartite, as it does not fit the definition.

1. Use BFS to traverse all the vertices.
2. Take a vertex and colour it red. (‘R’)
3. Colour all its neighbour vertices as (‘B’). (Blue = ‘B’ and Red = ‘R’)
4. Colour the next level vertices as (‘R’) and so, untill all vertices are coloured.
5. If at any step, we encounter contradicting colours, then the given graph to us is not bipartite!.
6. Hence, break and print “No” else print “Yes”;

Here is source code of the C++ Program to Check if a Given Graph is Bipartite. The program is successfully compiled and tested under Linux platform. The program output is also shown below.

#include<bits/stdc++.h>
 
using namespace std;
 
int n,e,i,j;
vector<vector<int> > graph;
vector<int> color;
bool vis[100011];
 
bool isBipartite()
{
    color[0] = 1; // Mark colour as 1 for first vertex.
    queue <int> q;
    q.push(0);
    while (!q.empty())
    {
        int temp = q.front();
        q.pop();
        for (i=0;i<n;i++)
        {
            if (graph[temp][i] && color[i] == -1) //if there is an edge, and colour is not assigned
            {
                color[i] = 1 - color[temp];
                q.push(i);
            }
            else if (graph[temp][i] && color[i] == color[temp]) // if there is an edge and both vertices have same colours
                return 0;                                   // graph is not bipartite
        }
    }
    return 1;
}
 
int main()
{
    int x,y;
    cout<<"Enter number of vertices and edges respectively:";
    cin>>n>>e;
    cout<<"\n";
    graph.resize(n);
    color.resize(n,-1);
    memset(vis,0,sizeof(vis));
    for(i=0;i<n;i++)
        graph[i].resize(n);
    for(i=0;i<e;i++)
    {
        cout<<"\nEnter edge vertices of edge "<<i+1<<" :";
        cin>>x>>y;
        x--; y--;
        graph[x][y]=1;
        graph[y][x]=1;
    }
    if(isBipartite())
        cout<<"Yes, The given graph is Bipartite.\n";
    else
        cout<<"No, The given graoh is not Bipartite.\n";
    return 0;
}

1. User must first enter the number of vertices, N, and then number of edges, E, in the graph.
2. It should be followed by E lines, denoting A and B, if there is an edge between A and B.
3. The graph is stored as adjacency matrix.
4. Then BFS is implemented using queue and colours are assigned to each vertex.
5. If a vertex is encountered second time, then we check its previous colour and new colour.
6. If new and previous colour differ, then given graph is not bipartite.

 
Case 1:
Enter number of vertices and edges respectively:6 5
 
 
Enter edge vertices of edge 1 :1 2
 
Enter edge vertices of edge 2 :1 3
 
Enter edge vertices of edge 3 :1 4
 
Enter edge vertices of edge 4 :1 5
 
Enter edge vertices of edge 5 :1 6
Yes, The given graph is Bipartite.
 
 
Case 2:
Enter number of vertices and edges respectively:5 5
 
 
Enter edge vertices of edge 1 :1 2
 
Enter edge vertices of edge 2 :1 3
 
Enter edge vertices of edge 3 :1 4
 
Enter edge vertices of edge 4 :1 5
 
Enter edge vertices of edge 5 :2 3
No, The given graoh is not Bipartite.

Sanfoundry Global Education & Learning Series – C++ Algorithms.
To practice all C++ Algorithms, here is complete set of 1000 C++ Algorithms.