This set of Discrete Mathematics Multiple Choice Questions & Answers (MCQs) focuses on “Graphs – Lattices”.
1. A Poset in which every pair of elements has both a least upper bound and a greatest lower bound is termed as _______
a) sublattice
b) lattice
c) trail
d) walk
View Answer
Explanation: A poset in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice. A lattice can contain sublattices which are subsets of that lattice.
2. In the poset (Z+, |) (where Z+ is the set of all positive integers and | is the divides relation) are the integers 9 and 351 comparable?
a) comparable
b) not comparable
c) comparable but not determined
d) determined but not comparable
View Answer
Explanation: The two integers 9 and 351 are comparable since 9|351 i.e, 9 divides 351. But 5 and 127 are not comparable since 5 | 127 i.e 5 does not divide 127.
3. If every two elements of a poset are comparable then the poset is called ________
a) sub ordered poset
b) totally ordered poset
c) sub lattice
d) semigroup
View Answer
Explanation: A poset (P, <=) is known as totally ordered if every two elements of the poset are comparable. “<=” is called a total order and a totally ordered set is also termed as a chain.
4. ______ and _______ are the two binary operations defined for lattices.
a) Join, meet
b) Addition, subtraction
c) Union, intersection
d) Multiplication, modulo division
View Answer
Explanation: Join and meet are the binary operations reserved for lattices. The join of two elements is their least upper bound. It is denoted by V, not to be confused with disjunction. The meet of two elements is their greatest lower bound. It is denoted by ∧ and not to be confused with a conjunction.
5. A ________ has a greatest element and a least element which satisfy 0<=a<=1 for every a in the lattice(say, L).
a) semilattice
b) join semilattice
c) meet semilattice
d) bounded lattice
View Answer
Explanation: A lattice that has additionally a supremum element and an infimum element which satisfy 0<=a<=1, for every an in the lattice is called a bounded lattice. A partially ordered set is a bounded lattice if and only if every finite set (including the empty set) of elements has a join and a meet.
6. The graph given below is an example of _________
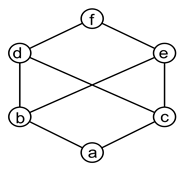
a) non-lattice poset
b) semilattice
c) partial lattice
d) bounded lattice
View Answer
Explanation: The graph is an example of non-lattice poset where b and c have common upper bounds d, e and f but none of them is the least upper bound.
7. A sublattice(say, S) of a lattice(say, L) is a convex sublattice of L if _________
a) x>=z, where x in S implies z in S, for every element x, y in L
b) x=y and y<=z, where x, y in S implies z in S, for every element x, y, z in L
c) x<=y<=z, where x, y in S implies z in S, for every element x, y, z in L
d) x=y and y>=z, where x, y in S implies z in S, for every element x, y, z in L
View Answer
Explanation: A sublattice S of a lattice L is a convex sublattice of L, if x ≤ z ≤ y and x, y in S implies that z belongs to S, for all elements x, y, z in L.
8. The graph is the smallest non-modular lattice N5. A lattice is _______ if and only if it does not have a _______ isomorphic to N5.
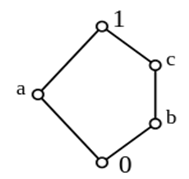
a) non-modular, complete lattice
b) moduler, semilattice
c) non-modular, sublattice
d) modular, sublattice
View Answer
Explanation: A lattice (L, ∨, ∧) is modular if for all elements a, b, c of L, the following identity holds->modular identity: (a ∧ c) ∨ (b ∧ c) = [(a ∧ c) ∨ b] ∧ c. This condition is equivalent to the following axiom -> modular law: a ≤ c implies a ∨ (b ∧ c) = (a ∨ b) ∧ c. A lattice is modular if and only if it does not have a sublattice isomorphic to N5.
9. Every poset that is a complete semilattice must always be a _______
a) sublattice
b) complete lattice
c) free lattice
d) partial lattice
View Answer
Explanation: A poset is called a complete lattice if all its subsets have both a join and a meet. Every complete lattice is a bounded lattice. Every poset that is a complete semilattice must always be a complete lattice.
10. A free semilattice has the _______ property.
a) intersection
b) commutative and associative
c) identity
d) universal
View Answer
Explanation: Any set X may be used to generate the free semilattice FX. The free semilattice is defined to consist of all of the finite subsets of X with the semilattice operation given by ordinary set union; the free semilattice has the universal property.
Sanfoundry Global Education & Learning Series – Discrete Mathematics.
To practice all areas of Discrete Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computer Science Books
- Apply for BCA Internship
- Practice Computer Science MCQs
- Check Discrete Mathematics Books
- Check BCA Books
