This set of Design of RC Structures Multiple Choice Questions & Answers (MCQs) focuses on “T-Beams – Lever Arm and Moment of Resistance”.
1. Which of the following is used to determine the moment of resistance of T-beam?
a) Total compression × Lever arm
b) Total compression ÷ Lever arm
c) Total compression – Lever arm
d) Total compression + Lever arm
View Answer
Explanation: The moment of resistance of the T-beam is found by multiplying the total compression and the lever arm. If the N.A. lies in the flange, the moment of resistance is given by:
Mr = bf × n × (c / 2)(d – (n / 3)).
2. Which of the following is not a problem of T-beam section?
a) Determination of moment of resistance of the given section
b) Design of section to resist a given bending moment
c) Determination of stresses in the section subjected to a given bending moment
d) Check for development length at supports
View Answer
Explanation: In T-beams there are three types of problems. The first is determination of MOR of the given section. Second is design of the section to resist a given bending moment. Third is determination of stresses in the given section subjected to a given bending moment.
3. An isolated T-beam, in the figure below, simply supported over a span of 6 m has following dimensions:
b = 750 mm,
Df = 125 mm,
d = 360 mm,
bw = 260 mm,
σcbc = 5 N/mm2
m = 19
What is the value of moment of resistance of the beam if mild steel bars are used?
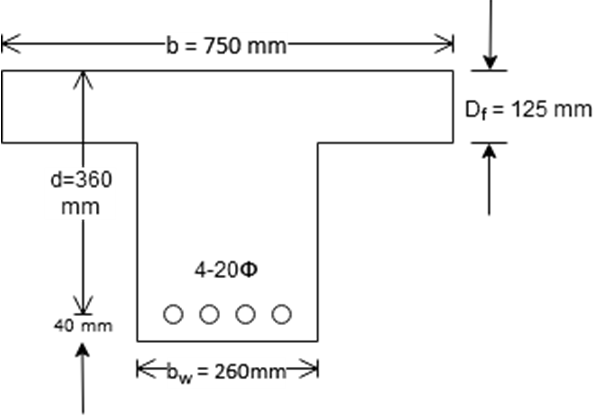
Fig. 1
a) 73.52 kN-m
b) 74.52 kN-m
c) 56.17 kN-m
d) 57.17 kN-m
View Answer
Explanation: Assume that N.A. lies in flange
Area of steel = Ast = 4×(π/4)(20)2 = 1250.6 mm2
For an isolated T-beam, effective flange width, bf = {l0/[(l0/b)+4]}+bw
= {6000/[(6000/750)+4]}+260 = 760mm
Available b = 750 mm, so bf = b = 750 mm
Equating the moments of equivalent areas about the N.A., we get
750×(n2/2) = 19×1250.6 (360-n)
n2 = 22920-63.67n
n = 122.90 mm
This is less than Df. The N.A. lies inside the flange.
For mild steel reinforcement:
nc = d/[1+(σst/mσcbc)] = 360/[1+(140/(19×5))] = 145.50 mm
The actual N.A. falls above the critical N.A., the section is under-reinforced. The stress in steel reaches its maximum value first. The stress in concrete is given by
c = (t/m)(n/(d-n)) = (140/19)(122.9/(360-122.9)) = 3.82 N/mm2
The MOR of the beam is given by
Mr = bf×n×(c/2)(d-(n/3)) = 750×122.9×3.82/2(360-(122.9/3))
= 56.17 kN-m.
4. In the given figure, an isolated T-beam carries an udl of 40 kN/m inclusive of its own weight over an effective span of 6 m. The beam has the following dimensions:
bf = b = 800 mm,
Df = 100 mm,
d = 480 mm,
bw = 300 mm,
M = 180 kN-m,
n = 187.80 mm,
σcbc = 5 N/mm2
σst = 140 N/mm2
m = 18
What are the necessary areas of tensile and compressive reinforcement?
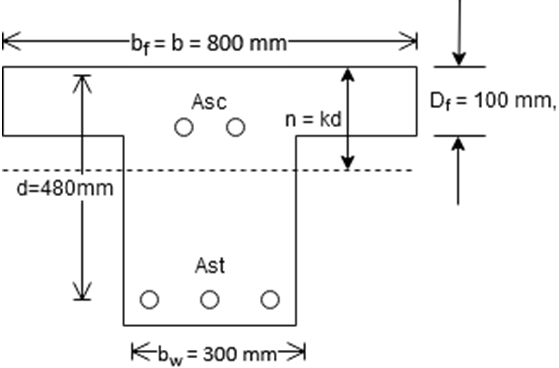
Fig. 2
a) 2941 mm2 and 1155 mm2
b) 2097 mm2 and 1155 mm2
c) 2097 mm2 and 844 mm2
d) 2941 mm2 and 1000 mm2
View Answer
Explanation: The MOR of the balanced section is
M1 = bf×Df(c/2)[(2kd-Df)/kd][d-(Df/2)+(Df2/6(2kd-Df))]
= 800×100×(5/2)[(2×187.8-100)/187.8]×[480-50+((100×100/6(2×187.8-100))
= 128 N-mm; a = 436
Ast1 = M1/(t×a) = 2097 mm2
M2 = M-M1 = (180-128)×106 = 52×106 N-mm
52×106 = (mc-1)Asc×c((kd-dc)/kd)(d-dc);dc = 40 mm
Asc = 1155 mm2
Ast1 = M2/(t(d-dc)) = 844 mm2
Total tensile steel Ast = 2097+844 = 2941 mm2
Comp. steel Asc = 1155 mm2
5. In a doubly reinforced T-beam section as shown below, the area of steel is 2260 mm2 and the area of concrete is 945 mm2. Taking σcbc = 5 N/mm2, σst = 140 N/mm2, m = 18. The dimensions of the section are:
bf = 912 mm,
b = 1200 mm,
Df = 100 mm,
d = 500 mm,
bw = 300 mm
What will be the MOR of the section neglecting web compression?
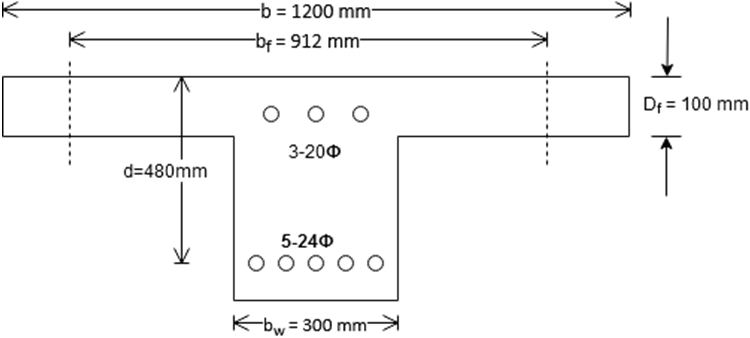
Fig. 3
a) 150 kN-m
b) 144.96 kN-m
c) 144.50 kN-m
d) 150.96 kN-m
View Answer
Explanation: Let the N.A. lie in the web at a distance n below the top of the flange. Taking the moment of equivalent areas about N.A. we get
bfDf(n-(Df/2))+(mc-1)Asc(n-dc) = mAst(d-n)
912×100(n-50)+(1.5×18-1)×945(n-40) = 18×2260(500-n)
n = 165.5 mm
Depth of critical N.A. nc = [mσcbc/(mσcbc+σst)]×d = 196 mm
Since actual N.A. falls above the critical N.A., the section is under-reinforced. Stress in steel will reach its maximum value first.
c = (t/m)(n/(d-n)) = (140/18)(165.5/(500-165.5)) = 3.848 n/mm2
The MOR is given by
Mr = bf×Df(c/2)[1+((2kd-Df)/kd)][d-(Df/2)+(Df2/6(2kd-Df))]×(mc-1)Asc×c((kd-dc)/kd)(d-dc)
= 912×100(3.848/2)[1+((165.5-100)/165.5)][500-50+(1002/6(2(165.5)-100))]×(1.5(18)-1)945×3.848((165.5-40)/165.5)(500-40)
= 144.56 kN-m
6. What is the expression for the lever arm (a) of a T-beam section?
a) [d-(Df/2)+(Df2/6(2n-Df))]
b) [d-(Df/2)+(Df2/6(2kd-Df))]
c) (d-0.42x)
d) (d-0.60x)
View Answer
Explanation: The lever arm of singly reinforced T-beam is given by:
[d-(Df/2)+(Df2/6(2n-Df))]
Here, [d-(Df/2)+(Df2/6(2kd-Df))] can be used for doubly reinforced T-beam.
The lever arm for rectangular section is given by (d-0.42x).
7. Which type of T-section has the actual N.A. (neutral axis) above the critical N.A.?
a) Singly reinforced
b) Under-Reinforced
c) Balanced
d) Over reinforced
View Answer
Explanation: If the actual N.A. is above the critical N.A., the section is under-reinforced. Here the stress in steel reaches its maximum permissible value first then the stress in concrete is found. If the actual N.A. falls at or below the critical N.A., the section is over-reinforced.
8. Which of the following is correct for determining the position of neutral axis?
a) By equating the moments of equivalent areas about the N.A.
b) On the basis of permissible stresses
c) By calculating actual stress in concrete
d) By calculating the maximum B.M. and equating it to MOR
View Answer
Explanation: The position of neutral axis is determined by equating the moments of equivalent areas about N.A., assuming the N.A. lies in the flange. The position of critical N.A. is determined on the basis of permissible stresses. When the actual N.A. lies above the critical N.A., the section is under reinforced. Steel reaches maximum stress first and the actual stress in concrete is then calculated.
Sanfoundry Global Education & Learning Series – Design of RC Structures
To practice all areas of Design of RC Structures, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
