Theory of Computation – Minimizing a Deterministic Finite Automata

In this tutorial we will learn how to minimize a DFA. It is important to minimize the DFA before its implementation. This saves space taken up by unnecessary states and transitions. For any regular language there exists a DFA with smallest number of states that accepts it. The procedure below will always produce the DFA with the smallest number of states from all sets of DFA that recognizes the language.

Minimization Algorithm for a DFA

1. Identify and remove the unreachable states. These states are the states with no incoming transition, but only outgoing transition.
2. Draw two transition tables T₁ and T₂ where T₁ contains all rows which contains states from Q-F and T₂ contains all the states from set F.
3. All trap states are indistinguishable. So we remove all the trap states except for the one with the lowest index and replace the trap states reference with the only trap state left.
4. Find the similar rows from T₁ such that the states after transition on a given input are same for those states. From the set of similar rows remove all the rows from the table except the one with the smallest index and make corresponding changes to the table.
5. Repeat the above step till all redundant rows have been eliminated.
6. Repeat step 4 and 5 for table T₂
7. Now combine the tables to get the minimized DFA.

This minimization process removes the non-reachable states, trap states and the indistinguishable states.

Question: Using the above procedure minimize the given DFA.

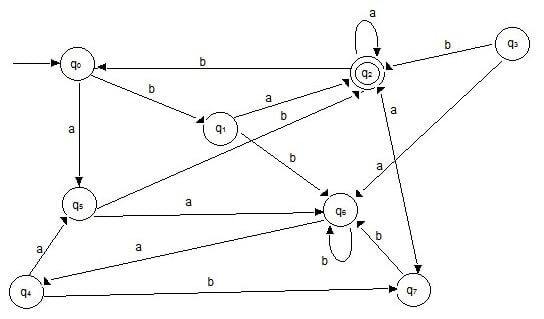
Solution:
Step 1: remove the unreachable states. In the above DFA q₃ is the only state that has no incoming edge, so we remove it.
Step 2: There are no trap states in the DFA.
Step 3: Transition tables
T₁

States	input a	input b
q0	q5	q1
q1	q2	q6
q4	q5	q7
q5	q6	q2
q6	q4	q6
q7	q2	q6

T₂

q2

q2

q0

Step 4:
Reducing the table by removing indistinguishable states
q₁ and q₇ are indistinguishable. Remove q₇ and replace reference of q₇ with q₁.

q0	q5	q1
q1	q2	q6
q4	q5	q1
q5	q6	q2
q6	q4	q6

Now q₀ and q₄ are indistinguishable. Remove q₄ and replace references of q₄ with q₀.

q0	q5	q1
q1	q2	q6
q5	q6	q2
q6	q0	q6

Step 6 : There is no indistinguishable state in set of final states so they remain unchanged
Step 7: Merging the two sets T₁ and T₂ so the final transition table for the DFA is :

q0	q5	q1
q1	q2	q6
*q2	q2	q0
q4	q5	q1
q5	q6	q2
q6	q4	q6

The final DFA after minimization :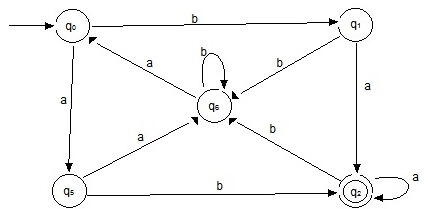

Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.

If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.