Theory of Computation – Nondeterministic Finite Automata with Null Transitions

An NFA with null transition is allowed to make transition not only on input from the alphabet but also with null input, i.e. without any input symbol. This transition without input is called null transition.
An NFA with null transition is also denoted by a 5-tuple
M = ( Q, Σ, δ, F q₀)
Where Q, Σ, q₀, F have their usual meaning and transition δ defines a mapping from Q x (Σ U {є})->2^Q

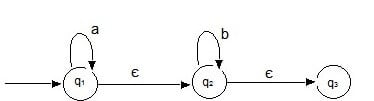
Consider the NFA in the above diagram. Null transition makes the designing of an NFA simpler as it reduces the complexity of the design and in some cases reduces the number of states too. In the above example for the NFA with null transition on giving input a to q₁ the set of states that the NFA is in is {q₂, q₃}. When a state is reached and if it has null transition the states that can be reached by the null transition are also included in the current set of states.

Null Closure

Let M = ( Q, Σ, δ, F q₀) be an NFA with null transitions, and let S be any subset of Q. The є- closure of S is the set є(s) defined as follows

1. Every element of S is an element of є(S);
2. For any q є є(s), every element of δ(q, є) is in є(S);
3. No other element of Q are in є(S)

In simple words, є(S) is set of all the states that can be reached from S without giving any input

Calculating null closure є (S)

Start with T = S. Make a sequence of passes, in each pass considering every q є T and adding to T all elements of δ(q, є) that are not already in T. Stop after any pass in which T does not change. The set є(S) is the final value of T.

Null closure for the given NFA
є (q₁) = {q₁, q₂, q₃}
є (q₂) = {q₂, q₃}
є (q₃) = {q₃}

Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.

If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.