This set of Digital Signal Processing Interview Questions & Answers focuses on “Linear Filtering Methods Based on DFT”.
1. By means of the DFT and IDFT, determine the response of the FIR filter with impulse response h(n)={1,2,3} to the input sequence x(n)={1,2,2,1}?
a) {1,4,11,9,8,3}
b) {1,4,9,11,8,3}
c) {1,4,9,11,3,8}
d) {1,4,9,3,8,11}
View Answer
Explanation: The input sequence has a length N=4 and impulse response has a length M=3. So, the response must have a length of 6(4+3-1).
We know that, Y(k)=X(k).H(k)
Thus we obtain Y(k)={36,-14.07-j17.48,j4,0.07+j0.515,0,0.07-j0.515,-j4,-14.07+j17.48}
By applying IDFT to the above sequence, we get y(n)={1,4,9,11,8,3,0,0}
Thus the output of the system is {1,4,9,11,8,3}.
2. What is the sequence y(n) that results from the use of four point DFTs if the impulse response is h(n)={1,2,3} and the input sequence x(n)={1,2,2,1}?
a) {9,9,7,11}
b) {1,4,9,11,8,3}
c) {7,9,7,11}
d) {9,7,9,11}
View Answer
Explanation: The four point DFT of h(n) is H(k)=1+2e-jkπ/2+3 e-jkπ (k=0,1,2,3)
Hence H(0)=6, H(1)=-2-j2, H(3)=2, H(4)=-2+j2
The four point DFT of x(n) is X(k)= 1+2e-jkπ/2+2 e-jkπ+3e-3jkπ/2(k=0,1,2,3)
Hence X(0)=6, X(1)=-1-j, X(2)=0, X(3)=-1+j
The product of these two four point DFTs is
Ŷ(0)=36, Ŷ(1)=j4, Ŷ(2)=0, Ŷ(3)=-j4
The four point IDFT yields ŷ(n)={9,7,9,11}
We can verify as follows
We know that from the previous question y(n)={1,4,9,11,8,3}
ŷ(0)=y(0)+y(4)=9
ŷ(1)=y(1)+y(5)=7
ŷ(2)=y(2)=9
ŷ(3)=y(3)=11.
3. Overlap add and Overlap save are the two methods for linear FIR filtering a long sequence on a block-by-block basis using DFT.
a) True
b) False
View Answer
Explanation: In these two methods, the input sequence is segmented into blocks and each block is processed via DFT and IDFT to produce a block of output data. The output blocks are fitted together to form an overall output sequence which is identical to the sequence obtained if the long block had been processed via time domain convolution. So, Overlap add and Overlap save are the two methods for linear FIR filtering a long sequence on a block-by-block basis using DFT.
4. In Overlap save method of long sequence filtering, what is the length of the input sequence block?
a) L+M+1
b) L+M
c) L+M-1
d) None of the mentioned
View Answer
Explanation: In this method, each data block consists of the last M-1 data points of the previous data block followed by L new data points to form a data sequence of length N=L+M-1.
5. In Overlap save method of long sequence filtering, how many zeros are appended to the impulse response of the FIR filter?
a) L+M
b) L
c) L+1
d) L-1
View Answer
Explanation: The impulse of the FIR filter is increased in length by appending L-1 zeros and an N-point DFT of the sequence is computed once and stored.
6. The first M-1 values of the output sequence in every step of Overlap save method of filtering of long sequence are discarded.
a) True
b) False
View Answer
Explanation: Since the data record of length N, the first M-1 points of ym(n) are corrupted by aliasing and must be discarded. The last L points of ym(n) are exactly as same as the result from linear convolution.
7. In Overlap add method, what is the length of the input data block?
a) L-1
b) L
c) L+1
d) None of the mentioned
View Answer
Explanation: In this method the size of the input data block is L points and the size of the DFTs and IDFT is N=L+M-1.
8. Which of the following is true in case of Overlap add method?
a) M zeros are appended at last of each data block
b) M zeros are appended at first of each data block
c) M-1 zeros are appended at last of each data block
d) M-1 zeros are appended at first of each data block
View Answer
Explanation: In Overlap add method, to each data block we append M-1 zeros at last and compute N point DFT, so that the length of the input sequence is L+M-1=N.
9. In which of the following methods, the input sequence is considered as shown in the below diagram?
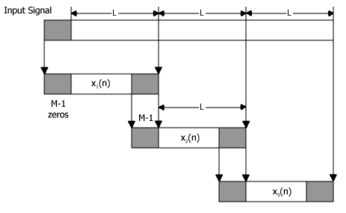
a) Overlap save method
b) Overlap add method
c) Overlap add & save method
d) None of the mentioned
View Answer
Explanation: From the figure given, we can notice that each data block consists of the last M-1 data points of the previous data block followed by L new data points to form a data sequence of length N+L+M-1 which is same as in the case of Overlap save method.
10. In which of the following methods, the output sequence is considered as shown in the below diagram?
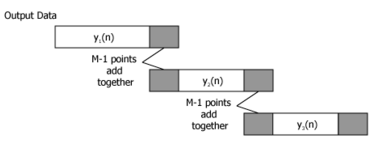
a) Overlap save method
b) Overlap add method
c) Overlap add & save method
d) None of the mentioned
View Answer
Explanation: From the figure given, it is clear that the last M-1 points of the first sequence and the first M-1 points of the next sequence are added and nothing is discarded because there is no aliasing in the input sequence. This is same as in the case of Overlap add method.
11. What is the value of x(n)*h(n), 0≤n≤11 for the sequences x(n)={1,2,0,-3,4,2,-1,1,-2,3,2,1,-3} and h(n)={1,1,1} if we perform using overlap add fast convolution technique?
a) {1,3,3,1,1,3,5,2,2,2,3,6}
b) {1,2,0,-3,4,2,-1,1,-2,3,2,1,-3}
c) {1,2,0,3,4,2,1,1,2,3,2,1,3}
d) {1,3,3,-1,1,3,5,2,-2,2,3,6}
View Answer
Explanation: Since M=3, we chose the transform length for DFT and IDFT computations as L=2M=23=8.
Since L=M+N-1, we get N=6.
According to Overlap add method, we get
x1‘(n)={1,2,0,-3,4,2,0,0} and h'(n)={1,1,1,0,0,0,0,0}
y1(n)=x1‘(n)*N h'(n) (circular convolution)={1,3,3,-1,1,3,6,2}
x2‘(n)={-1,1,-2,3,2,1,0,0} and h'(n)={1,1,1,0,0,0,0,0}
y2(n) = x2‘(n)*N h'(n)={-1,0,-2,2,3,6,3,1}
Thus we get, y(n) = {1,3,3,-1,1,3,5,2,-2,2,3,6}.
12. What is the value of x(n)*h(n), 0≤n≤11 for the sequences x(n)={1,2,0,-3,4,2,-1,1,-2,3,2,1,-3} and h(n)={1,1,1} if we perform using overlap save fast convolution technique?
a) {1,3,3,-1,1,3,5,2,-2,2,3,6}
b) {1,2,0,-3,4,2,-1,1,-2,3,2,1,-3}
c) {1,2,0,3,4,2,1,1,2,3,2,1,3}
d) {1,3,3,1,1,3,5,2,2,2,3,6}
View Answer
Explanation: Since M=3, we chose the transform length for DFT and IDFT computations as L=2M=23=8.
Since L=M+N-1, we get N=6.
According to Overlap save technique, we get
x1‘(n)={0,0,1,2,0,-3,4,2} and h'(n)={1,1,1,0,0,0,0,0}
=>y1(n)={1,3,3,-1,1,3}
x2‘(n)={4,2,-1,1,-2,3,2,1} and h'(n)={1,1,1,0,0,0,0,0}
=>y2(n)={5,2,-2,2,3,6}
=>y(n)= {1,3,3,-1,1,3,5,2,-2,2,3,6}.
Sanfoundry Global Education & Learning Series – Digital Signal Processing.
To practice all areas of Digital Signal Processing for interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
