This set of Phase Transformation online quiz focuses on “Thermodynamics and Phase Diagrams – Single Component System”.
1. The slope of the H-T curve is ________
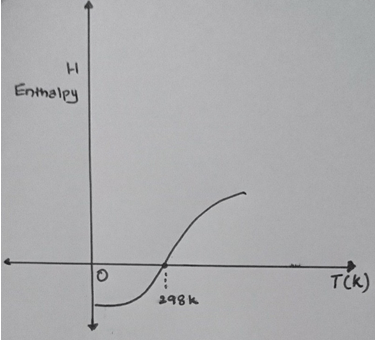
a) Specific heat CV
b) Pressure
c) Volume
d) Specific heat CP
View Answer
Explanation: The slope of the graph gives the value of specific heat Cp. As dH/dt for pure metal gives the CP value. CP is actually the specific heat of the gas at constant pressure and interestingly solids and fluids are having only a single value for specific heat.
2. Reason why in many metals, we find the phase with a relatively closely packed structure is stable at a lower temperature, whereas a relatively loosely packed structure is stable at higher temperature?
a) Enthalpy
b) Volume
c) Entropy term
d) Temperature
View Answer
Explanation: The increasing importance of the entropy term that is –TS is the reason behind the stability of closely packed structure at relatively low temperature and as the temperature increases the entropy term increases because of increase in T hence the randomness increases and hence the movement of individual particle increases which creates a kind of instability in closely packed structure at high temperature.
3. At all temperatures the liquid has a higher enthalpy than solid.
a) True
b) False
View Answer
Explanation: Liquid absorbs more heat and they covet their gained heat into higher vibrational and translational molecular motion, hence at temperatures the liquid has a higher enthalpy than solid.
4. Iron exist as BCC ferrite at temperature____________
a) Above 910 degree Celsius
b) Below 910 degree Celsius
c) Below 1000 degree Celsius
d) Above 1000 degree Celsius
View Answer
Explanation: At atmospheric pressure iron can exist as either BCC ferrite below 910 degree Celsius or FCC austenite above 910, and at 910 degree Celsius both phases can exist in equilibrium.
5. Which of the following is a spontaneous exothermic process?
a) Rusting
b) Ice melting
c) Removal of sugar from the coffee
d) Dissolution of sand in water
View Answer
Explanation: Rusting is spontaneous exothermal process .Melting of ice is a spontaneous endothermic process and the last two are non-spontaneous in nature.
6. A liquid metal is undercooled by ΔT below Tm before it solidifies, solidification will be accompanied by _____
a) A constant free energy
b) An increase in free energy
c) A decrease in free energy
d) ΔG=0
View Answer
Explanation: There will be a decrease in free energy. The decrease in free energy provides the driving force for solidification. To get the solidification process started, the liquid phase must be undercooled, cooled to a temperature below the freezing point.
7. Which rule states that the entropy of fusion is a constant ==<R (8.3 J mol-1 K-1) for most metals?
a) Richards rule
b) Stefan’s Rule
c) Charles law
d) Fermat’s rule
View Answer
Explanation: Richards rule states that the entropy of fusion is a constant for most metals. Fermat’s rule helped in finding the greatest and smallest ordinates in curved lines and Charles law states that pressure remaining constant, the volume of a given mass of gas increases or decreases by 1/273 part of its volume at 0 degree Celsius for each degree Celsius rise or fall of its temperature.
8. The enthalpy of a phase which is stable at higher temperature is higher (less negative) than that of a phase which is stable at lower temperature.
a) True
b) False
View Answer
Explanation: The enthalpy of a phase which is stable at higher temperature is higher because ΔH value is greater than 0 that is H1-H2>0(H1 and H2 represent gamma and alpha phase respectively).
9. What happens to the internal energy of a system with constant volume and constant entropy during a spontaneous process?
a) Increases first then decreases
b) Decreases
c) Remains same
d) Increases
View Answer
Explanation: Internal energy of the system decreases. This in fact a statement about entropy since it states that if the entropy of the system remains unchanged in the transformation, there must be an increase in the entropy of the environment caused by the outflow of heat from the system.
10. Which of the following structure is stable at low temperature?
a) α-TI with BCC structure
b) β-TI with HCP structure
c) β-TI with BCC structure
d) α-TI with HCP structure
View Answer
Explanation: The reason for this lies in a more closely packed structure where there is a lesser degree of vibrational freedom, hence it makes α-TI with HCP structure stable at low temperature.
Sanfoundry Global Education & Learning Series – Phase Transformation.
To practice all areas of Phase Transformation for online Quizzes, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Phase Transformation Books
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Mechanical Engineering Books
- Practice Metallurgical Engineering MCQs
