1. Which of the following term correctly represents transient nature of a process?
a) Steady state
b) Unsteady state
c) Process with dead lag
d) Exponential behavior of process
View Answer
Explanation: Transients nature in a chemical process refers to a segment of the activity which is lasting for only a short time. For a chemical process plant, during plant start up, the initial process is unsteady i.e., transient. So, transient is correctly defined by unsteady state of a process.
2. Which of the following conservation balancing equations is required for modelling a heater system?
a) Heat and Energy balance
b) Heat and Mass balance
c) Mass and matter balance
d) Heat and Concentration balance
View Answer
Explanation: In a heating system, we need to perform mass and energy balancing for modelling the system. Concentration and heat balancing are not required in heating system. Neither is matter.
3. Which of the following correctly represent the components of a control system?
a) Thermocouple, displacer device, heating coil
b) Measuring element, thermometer, pressure gauge
c) Process, measuring element, controller and final control element
d) Process, measuring element, amplifier and final control element
View Answer
Explanation: Every control system consists of a process, measuring element, controller and final control element. Pressure gauge, thermocouple and displacer device all are measuring devices.
4. What is the nature of curve for exit concentration of a perfectly mixing system?
a) Parabolical
b) Hyperbolical
c) Positive exponential
d) Negative exponential
View Answer
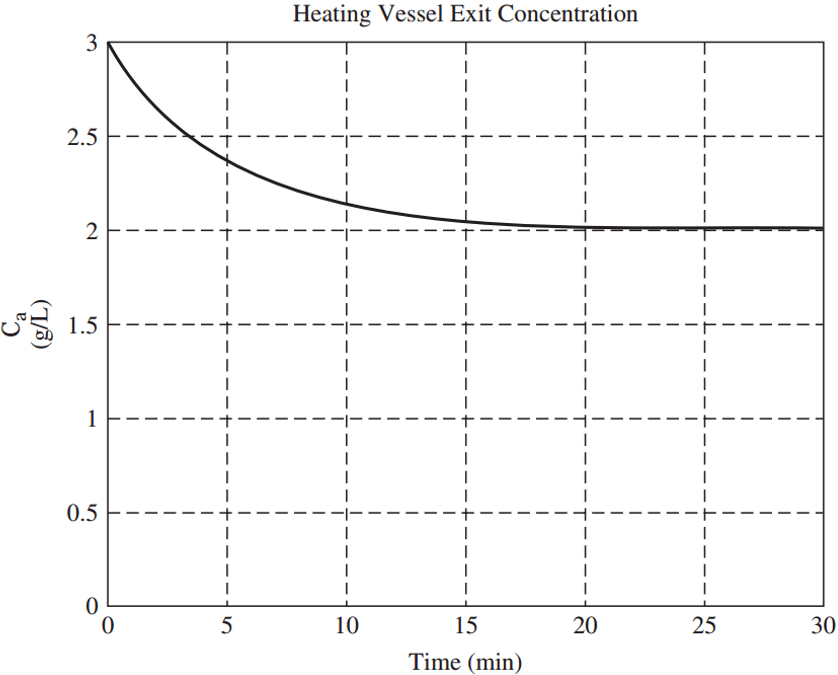
Explanation: The exit concentration of heater system has the equation
C = CF + e-t/T, where t is time and T is time constant.
The attached figure is the graphical representation of the equation for CF = 2g / L(say).
5. What is the nature of curve for exit temperature of a perfectly mixing system?
a) Parabolical
b) Hyperbolical
c) Positive exponential
d) Negative exponential
View Answer
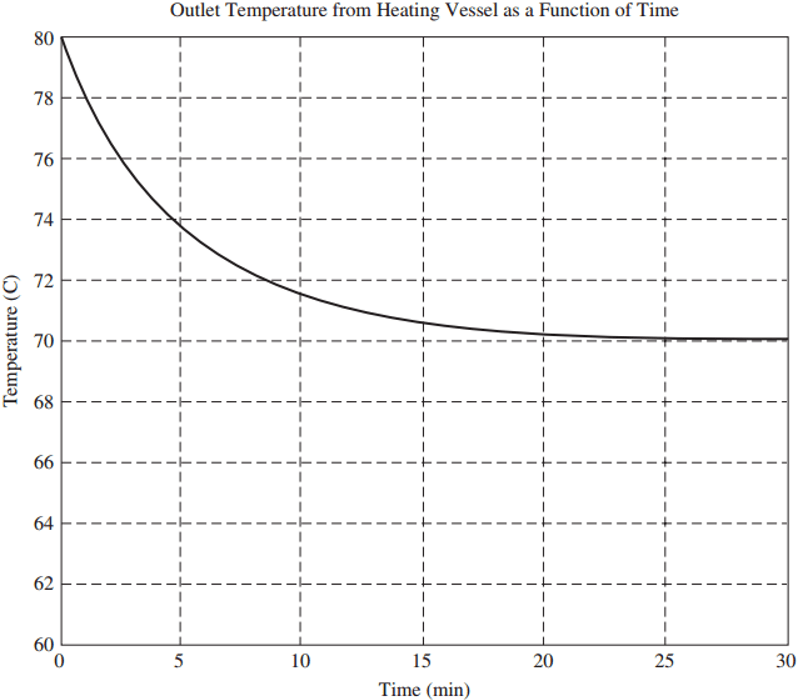
Explanation: The exit temperature of heater system has the equation
T = TF + Ke-t/₸, where t is time, K is constant and ₸ is time constant.
The attached figure is the graphical representation of the equation for TF = 70°C(say).
6. Which of the following assumptions are made for a simple perfectly mixing and heater system?
a) There is only one heating source and the concentration is uniform throughout the system
b) There is only one heating source and the concentration is not uniform throughout the system
c) There are multiple heating source and the concentration is uniform throughout the system
d) There are multiple heating source and the concentration is not uniform throughout the system
View Answer
Explanation: The concentration is uniform in a perfectly mixed model. For a simple heater, we consider only one heating source. For complex models, multiple heating sources are used.
Process Control MCQ on Tools for Modeling
7. Which of the following correctly represents the laplace transform of sin(wt)?
a) w / (s2 + w2)
b) s2 / (s2 + w2)
c) (s2 + w2) / (1 + w2)
d) w2 / (s2 + w2)
View Answer
Explanation: According to the first principle of laplace transform, F(s) = \(∫_0^∞\)f(t) e-stdt
Hence for f(t) = Sin(wt),
F(s) = L[f(t)] = \(∫_0^∞\)sin(wt)e-stdt
Now we know, sin(wt) = \(\frac {1}{2i}\)(eiωt – e-iωt)
So, substituting the value of sin(wt) in F(s) we get,
F(s) = L[f(t)] = \(\int_0^∞ \frac {1}{2i}\)(eiωt – e-iωt)e-stdt
= \(\frac {1}{2i} \big [ \frac {e^{-(s-iω)t}}{-(s-iw)} – \frac {e^{-(s + iω)t}}{-(s + iw)} \big ] \)(∞,0)
= \(\frac {1}{2i} \big [ \frac {1}{s-iw} – \frac {1}{s + iw} \big ] \)
= w / (s2 + w2)
Hence, L[f(t)] = w / (s2 + w2).
8. Which of the following is true regarding laplace transform?
a) L{af1(t) + bf2(t)} = aL{f1(t)} + bL{f2(t)}
b) L{af1(t) + bf1(t)} = aL{f1(t)} + bL{f2(t)}
c) L{bf1(t) + af2(t)} = aL{f1(t)} + bL{f2(t)}
d) L{af1(t) + bf2(t)} = abL{f1(t)} + abL{f2(t)}
View Answer
Explanation: The Laplace transform is linear. In mathematical notation, this means L{af1(t) + bf2(t)} = aL{f1(t)} + bL{f2(t)} where a and b are two constants and f1 and f2 are two functions of time.
9. Which of the following correctly represent the ramp function of a system?
a) f(t) = tu(t)
b) f(t) = u(t)
c) f(t) = e-tu(t)
d) f(t) = te-tu(t)
View Answer
Explanation: u(t) represents unit step input. tu(t) is the ramp input. e-tu(t) is the exponential function and te-tu(t) is the exponential ramp input.
10. Which of the options correctly represents the function shown in the following figure?
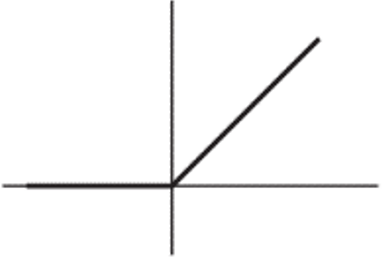
a) Parabolical
b) Hyperbolical
c) Positive exponential
d) Ramp
View Answer
Explanation: The given figure has a linear behavior with no bounded output. Such behavior is exhibited by ramp function. Hence the figure represents the ramp function.
11. Which of the options correctly represents the function shown in the following figure?
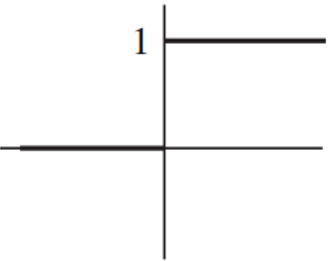
a) Ramp
b) Hyperbolical
c) Positive exponential
d) Unit step
View Answer
Explanation: From the figure it is clear that at t = 0, there is a shift of the curve from 0 to 1 and the nature is a sustained one. Such behavior is exhibited by unit step function. Hence the figure represents the unit step function.
12. Which of the options correctly represents the function shown in the following figure?
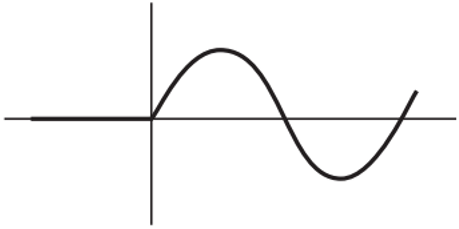
a) Ramp
b) Hyperbolical
c) Sinusoidal
d) Unit step
View Answer
Explanation: The behavior of the curve is sinusoidal. Ramp follows a linear pattern. Unit step is sudden rise in set point.
13. What is the area under a unit impulse?
a) 1
b) Infinite
c) 0
d) < 0
View Answer
Explanation: For a unit impulse function, the area under the curve is 1. The laplace transform of unit impulse function is 1.
14. What is the laplace transform of tn?
a) n! / (sn+1)
b) n! / (sn)
c) 0
d) (n + 1)! / (sn+1)
View Answer
Explanation: According to the first principle of laplace transform F(s) = \(∫_0^∞\)f(t) e-stdt
So, L(tn) = \(∫_0^∞\)tn e-stdt
Integrating by parts we get,
∫ tn e-stdt = -tn\(\frac {e^{-st}}{ s} + \frac {1}{s} \)∫ntn e-stdt
∫ tn e-stdt = limc → ∞\( \big ( \frac {1}{s}\) tn e-st \( \big )\)(c, ∞) + \( \frac {n}{s}\) L(tn-1)(s)
In order for this limit to exist, we again must insist that s not equal to 0 and that s > 0 so that e-s∞ has a limit (of zero). Using L’Hospital’s rule n times, we see that
limc → ∞\( \big ( – \frac {1}{s}\) cn e-sc \(\big )\) = 0
Hence, L(tn) = n! / (sn+1).
Process Control MCQ on Ordinary Differential Equation
15. Which of the following is necessary to determine the solution ODE using laplace transform?
a) Initial and final boundary condition
b) Initial boundary condition
c) Final boundary condition
d) First order derivative
View Answer
Explanation: The laplace transform of the ODE results in the formation of an initial value of the independent variable term. The value of the same needs to be provided in order to solve the ODE.
16. Which of the following pair of methods are used for solution of ODE by laplace?
a) Heaviside method and Tarsen method
b) Heaviside method and partial fraction
c) Partial method and Tarsen method
d) Heaviside method and Newton’s method
View Answer
Explanation: In both Heaviside and partial method we get the ODE in form of fractions. Laplace operations can be easily applied on the fractions to solve the differential equations.
17. Which of the following correctly represents the solution of the differential equation \(\frac {dx}{dy}\) + 3x = 0 with x(0) = 2?
a) 2e-3t
b) 2e-4t
c) e-3t
d) 3e-3t
View Answer
Explanation: Performing laplace operation of \(\frac {dx}{dy}\) + 3x = 0 we get,
L[\(\frac {dx}{dy}\) + 3x] = 0
sx(s) – x(0) + 3x(s) = 0 [ since, L(\(\frac {dx}{dy}\)) = sx(s) – x(0) and L(x) = x(s)]
x(s) = \(\frac {2}{s + 3}\) [since x(0) = 2]
Performing laplace inverse we get,
X(t) = 2e-3t [ since L-1(\(\frac {1}{s + 3}\)) = e-3t]
18. Which of the following options correctly represents the chemical mixer to determine the transform of the exit concentration and temperature?
a) Mass and energy balance
b) Mass balance
c) Energy balance
d) Concentration and energy balance
View Answer
Explanation: Only mass balance and only energy balance is not sufficient for forming the model of the mixer. Hence, the model can be formed by combining both the energy and mass balance equations.
19. Which of the options correctly represents the laplace inverse of 2 / s3?
a) t2
b) t3
c) t-2
d) t-3
View Answer
Explanation: We know Laplace of tn i.e. L[tn] = n! / sn+1. So putting n = 2 and performing Laplace inverse we get,
L-1[2! / s2+1]
= L-1[ 2 / s3]
= 2 × t2 / 2
= t2
Process Control MCQ on Partial Fractions
20. Which of the following is necessary to solve the roots of a differential equation using Laplace transform method?
a) Numerator of x(s) should be made equal to zero
b) Denominator of x(s) should be made equal to zero
c) Numerator of the transfer function should be made equal to infinite
d) Numerator of the transfer function should be made imaginary
View Answer
Explanation: To determine the roots of the differential equation using Laplace transform method, it is necessary to put the numerator of x(s) as zero. Consequently, the roots can be determined.
21. Which of the following is correct regarding the stability of a system?
a) The roots of the equation should lie on the left half plane
b) The roots of the equation should lie on the right half plane
c) The roots of the equation should lie on the imaginary plane
d) The roots of the equation should lie on the origin
View Answer
Explanation: For a system to be stable, the roots of an equation should lie on the left half plane. If the roots lie on the right half plane, system will be unstable. Roots on the origin indicate integrating response.
22. Which of the following correctly represents the nature of the system when the roots lie on the imaginary plane?
a) Oscillatory
b) Stable
c) Infinite response
d) Unstable
View Answer
Explanation: When the roots of a system lie on the imaginary plane then the nature of the system is oscillatory due to low damping. System is stable when the roots are on the left half plane. System is unstable when the roots are on the right half plane.
23. How many initial conditions are required to solve a differential equation using Laplace of order 2?
a) One
b) Two
c) Three
d) Four
View Answer
Explanation: If we assume a differential equation like the following one:
\(\frac {d^2 y}{dx^2} + \frac {dy}{dx}\)+y = 1
We can see that for solving using Laplace transform, we need at least two initial conditions. This can be explained below.
If we take Laplace transform the differential equation we will get,
S2y(s)-Sy(0)-y’(0)+Sy(s)-y(0)+y(s) = \(\frac {1}{S}\) {Since, L[ \(\frac {d^2 y}{dx^2}\) ] = S2y(s)-Sy(0)-y’(0)}
Thus, we can see that we need the value of y(0) and y’(0) to solve the equation. Thus, two initial conditions are required.
Process Control MCQ on Transfer Function
24. Which of the following system correctly represent a first order system?
a) Bare mercury thermometer
b) U – tube manometer
c) Switch
d) Two mixing tanks in series
View Answer
Explanation: For a mercury thermometer,
hA(x – y) = mC\(\frac {dy}{dx}\) [where h is the heat transfer coefficient, A is surface area of bulb for heat transfer, m is the mass of mercury in bulb, C is the heat capacity of mercury, x is the thermometer reading and y is the temperature input]
Let xs and ys be the steady state values of x and y respectively.
At steady state, xs = ys = 0.
Hence, hA{(x – xs) – (y – ys)} = mC\(\frac {d(y – ys)}{dx}\).
Or, hA(X – Y) = mC\(\frac {d(Y)}{dx}\). [x – xs = X, y – ys = Y]
Using laplace transform for the equation we get,
hA{X(s) – Y(s)} = mC{Y(s) – Y(o)}
or, \(\frac {hA}{mC}\)X(s) – \(\frac {hA}{mC}\)Y(s) = Y(s) [ since Y(0) = 0]
or, \(\frac {Y(s)}{X(s)} = \frac {1}{TS + 1}\) [Let \(\frac {mC}{hA}\) = T]
Which is an equation of first order system.
25. Which of the following is correct assumption regarding the analysis of first order system using mercury thermometer?
a) All the resistance to heat transfer resides in the film surrounding the bulb
b) All the resistance to heat transfer resides outside the film surrounding the bulb
c) All the resistance to mass transfer resides in the film surrounding the bulb
d) All the resistance to mass transfer resides outside the film surrounding the bulb
View Answer
Explanation: The resistance offered by the glass and mercury is neglected. All the resistance to heat transfer is assumed to reside in the film surrounding the bulb. Mass transfer phenomena is not related to this context.
26. Which of the following correctly represent the order of the thermometer when it is surrounded by a cover?
a) First
b) Second
c) Third
d) Fourth
View Answer
Explanation: When we use a bare thermometer then it is a first order system. Any thermometer with a cover on it will behave as an order higher than first order normally second.
27. Which of the following two models is correct for lumped parameter type?
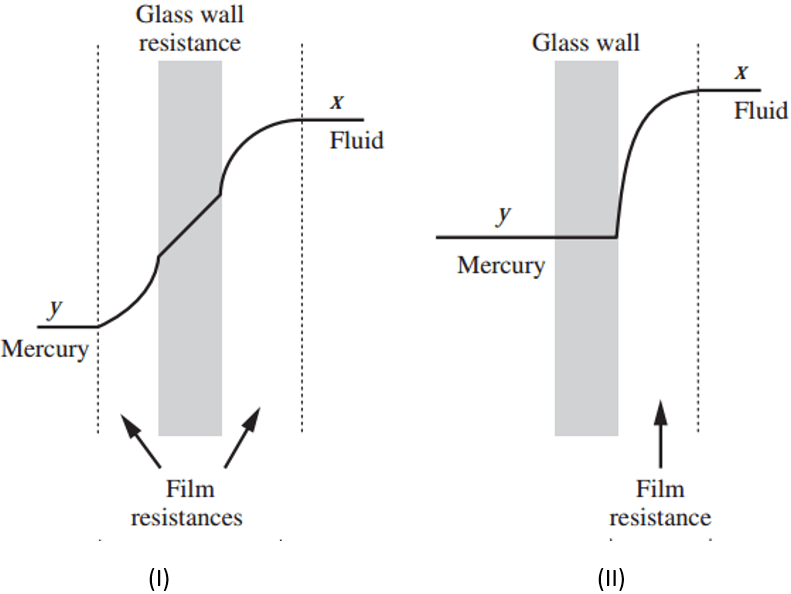
a) (I)
b) (II)
c) Both (I) and (II)
d) Lumped parameter model cannot be applied for mercury thermometer
View Answer
Explanation: Model (I) is the actual temperature profile where the profile shows the temperature gradient. In model (II) all the resistance is assumed to be in the film resistance only for which it behaves as a lumped parameter model.
28. Which of the following correctly represents the time constant of a first order system?
a) Time constant of a first order system is the time required at which the ultimate value is 63.2% of the set point value
b) Time constant of a first order system is the time required at which the ultimate value is 33.2% of the set point value
c) Time constant of a first order system is the time required at which the set point value is 63.2% of the ultimate value
d) Time constant of a first order system is the time required at which the ultimate value is 100% of the set point value
View Answer
Explanation: For a first order system,
\(\frac {Y(t)}{x(t)}\) = (1 – e-t/T) [T is the time constant, t is the time]
For a unit step input,
X(t) = 1
Y(t) = (1 – e-t/T)
For t = T,
Y(t) = (1 – e-T/T)
= 1 – 0.367
= 0.632
Which is the 63.2% of the ultimate value.
29. Which of the following correctly represents the general form for a first – order system?
a) T \(\frac {dy}{dt}\) + Y(t) = Kpx(t)
b) T2 \(\frac {dy}{dt}\) + Y(t) = Kpx(t)
c) T3 \(\frac {dy}{dt}\) + Y(t) = Kpx(t)
d) T4 \(\frac {dy}{dt}\) + Y(t) = Kpx(t)
View Answer
Explanation: For a first order system,
Y(s) / X(s) = \(\frac {1}{TS + 1}\)
Hence, T2 T3 T4 as coefficients of \(\frac {dy}{dt}\) are not correct.
30. Which of the following statement is correct?
a) A transfer function relates two variables in a physical process; one of these is the cause and the other is the effect
b) A transfer function relates two variables in a physical process; one of these is the effect and the other is the resultant of effect
c) A transfer function relates two variables in a physical process; one of these is the effect and the other is the product of effect and cause
d) A transfer function relates two variables in a physical process; one of these is the cause and the other is the resultant of cause
View Answer
Explanation: Transfer function is the ratio of the output to input of a system in s domain. Hence transfer function relates two variables in a physical process; one of these is the effect and the other is the resultant of effect.
31. Which of the following is correct relation of transfer function for the below mentioned figure?
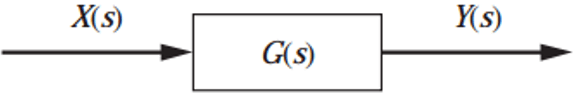
a) G(s) = Y(s) / X(s)
b) G(s) = Y(s) × X(s)
c) G(s) = Y(s) + X(s)
d) G(s) = Y(s) – X(s)
View Answer
Explanation: Transfer function is the ratio of the output to input in s domain. Y(s) is the output and X(s) is the input. Hence the transfer function is Y(s) / X(s).
32. Which of the following is correct for initial value theorem?
a) limt→0f(t) = S lims→∞f(s)
b) limt→∞f(t) = S lims→∞f(s)
c) limt→∞f(t) = S lims→0f(s)
d) limt→0f(t) = S lims→0f(s)
View Answer
Explanation: Initial value means at time t→0. The corresponding value in s domain will be s→∞. t→∞ is not possible in this context.
33. Which of the following is correct for final value theorem?
a) limt→0f(t) = S lims→∞f(s)
b) limt→∞f(t) = S lims→∞f(s)
c) limt→∞f(t) = S lims→0f(s)
d) limt→0f(t) = S lims→0f(s)
View Answer
Explanation: Final value means at t→∞. The corresponding value in s domain will be s→0. t→0 is not possible in this context.
34. Which of the following is the correct definition of transient response?
a) A transient response is the response of a system to a change from an unsteady state
b) A transient response is the response of a system to a change from an equilibrium or a steady state
c) A transient response is the input of a system to a result from an equilibrium or a steady state
d) A transient response is the input of a system to a result from an unsteady state
View Answer
Explanation: When a process is perturbed from its steady state, then the system tr to regain its steady state and transient response is the response of a system to a change from an equilibrium or a steady state.
Process Control MCQ on Forcing Functions
35. Which of the following options correctly represent the list of forcing function?
a) Step, impulse, ramp, and sinusoidal
b) Step, impulse, complex number
c) Step, impulse, ramp, and complex number
d) Step, complex number, ramp, and sinusoidal
View Answer
Explanation: Complex number is not a forcing function. Ramp is a forcing function. Step and sinusoidal are also forcing function.
36. Which of the following options is correct for the input shown below?
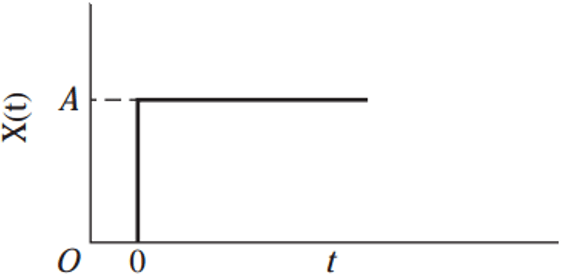
a) Step
b) Ramp
c) Sine
d) Impulse
View Answer
Explanation: From the graph we can see that the response rises upto a magnitude of A at time t = 0 and then it is sustained. Such type of behavior is shown by step function. Hence step input is the correct answer.
37. Which of the following options is correct for the input shown below?
a) Step
b) Ramp
c) Sine
d) Pulse
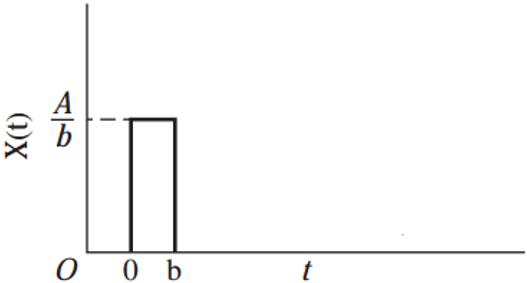
View Answer
Explanation: From the graph we can see that the response first rises upto a magnitude of A / b at time t = 0 and then after time t = b, the response again returns back to its original value. Such type of behavior is shown by pulse.
38. Which of the following options is correct for the input shown below?
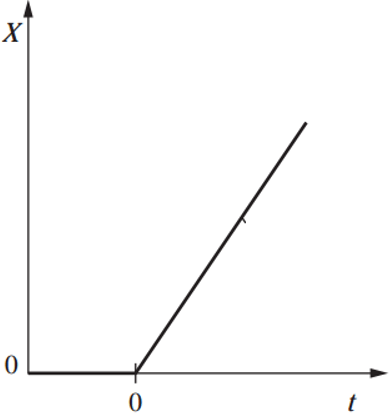
a) Step
b) Ramp
c) Sine
d) Pulse
View Answer
Explanation: From the graph we can see that the response is linear from time t = 0 and fully unbounded. Such type of behavior is shown by ramp function. Hence, ramp input is the correct answer.
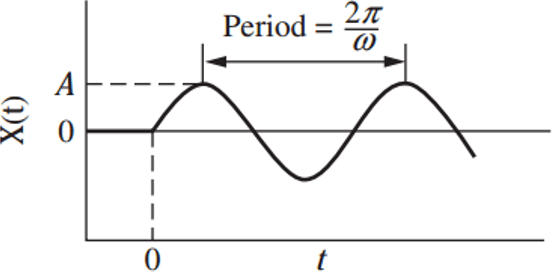
39. Which of the following correctly represents the time constant of a first order system?
a) Step
b) Ramp
c) Sine
d) Pulse
View Answer
Explanation: From the graph we can see that the response has peaks having maximum magnitude of A and minimum – A. The period of oscillation is \(\frac {2π}{ω}\). Thus, the nature of the graph is sinusoidal.
40. Which of the following correctly represents the input x(t) = Au(t)?
a) Step
b) Ramp
c) Cosine
d) Sine
View Answer
Explanation: Ramp is represented by x(t) = tu(t). Sine and cosines are having different form. Hence, x(t) = Au(t) is the input for step function of magnitude A.
41. Which of the following correctly represents the input x(t) = tu(t)?
a) Step
b) Ramp
c) Cosine
d) Sine
View Answer
Explanation: The input function represents a ramp since the function represents a linear form and ramp input is a linear input. Unit Step function is represented by x(t) = u(t). Sine is represented by x(t) = A Sin(ωt), where A is the magnitude of oscillation.
42. Which of the following represents the Laplace of unit step function i.e., L[u(t)]?
a) 1 / s
b) 1 / s2
c) 1
d) s2
View Answer
Explanation: According to the first principle of Laplace transform, F(s) = \(∫_0^∞\)f(t) e-st dt.
43. Which of the options correctly represent the output for the graph?
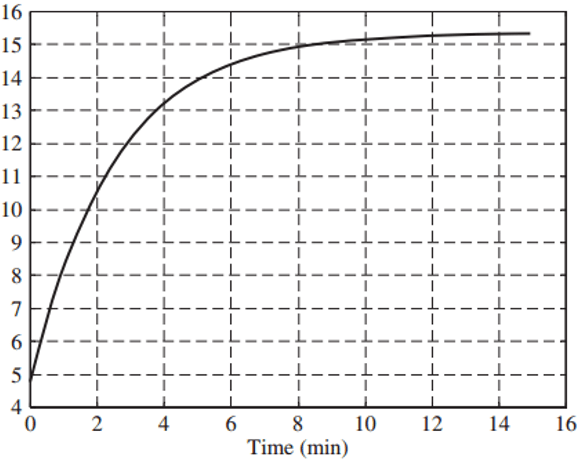
a) First order
b) Second Order
c) Third Order
d) Zero order
View Answer
Explanation: For a first order system, y(t) = 1 – e-t/T.
Now for t = T, y(t) = 1 – e-1.
Or, y(t) = 0.632.
Now 0.632 of the final value i.e., 0.632 times of 16 is 10.11 which is achieved at time t = 1.8, which can be interpreted from the graph. Hence it is a first order output.
44. For a thermometer, if the step change in input is 50 unit, the time is equal to time constant, what is the value the output?
a) 31.606
b) 42.501
c) 39.563
d) 50.214
View Answer
Explanation: For a first order system, Y(t) / x(t) = 1 – e-t/T
Step change in input is 50. So, x(t) = 50.
For t = T, Y(t) = 50(1 – e-1)
Thus, Y(t) = 50 × 0.632
= 31.606
More MCQs on Process Control:
- Process Control MCQ (Set 2)
- Process Control MCQ (Set 3)
- Process Control MCQ (Set 4)
- Process Control MCQ (Set 5)
- Process Control MCQ (Set 6)
- Process Control MCQ (Set 7)
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
