This set of Probability and Statistics Multiple Choice Questions & Answers (MCQs) focuses on “Gamma Distribution”.
1. The mean and the variance for gamma distribution are __________
a) E(X) = 1/λ, Var(X) = α/λ2
b) E(X) = α/λ, Var(X) = 1/λ2
c) E(X) = α/λ, Var(X) = α/λ2
d) E(X) = αλ, Var(X) = αλ2
View Answer
Explanation: The mean and the variance for gamma distribution is given as
E(X) = α/λ, Var(X) = 1/λ2.
2. Putting α=1 in Gamma distribution results in _______
a) Exponential Distribution
b) Normal Distribution
c) Poisson Distribution
d) Binomial Distribution
View Answer
Explanation: f (x) = λα xα−1 e−λx / Γ(α) for x > 0
= 0 otherwise
If we let α=1, we obtain
f(x) = λe−λx for x > 0
= 0 otherwise.
Hence we obtain Exponential Distribution.
3. Sum of n independent Exponential random variables (λ) results in __________
a) Uniform random variable
b) Binomial random variable
c) Gamma random variable
d) Normal random variable
View Answer
Explanation: Gamma (1,λ) = Exponential (λ).
Hence Exponential (λ1) + Exponential (λ2) + Exponential (λ3)….. n times = Gamma(n,λ).
4. Find the value of Γ(5/2).
a) 5/4 . π1/2
b) 7/4 . π1/2
c) 1/4 . π1/2
d) 3/4 . π1/2
View Answer
Explanation: By the property of Gamma Function
Γ(α+1) = αΓ(α)
\(Γ(\frac{5}{2}) = \frac{3}{2} ⋅ Γ(\frac{3}{2}) \)
\(= \frac{3}{2} ⋅ \frac{1}{2} . Γ(\frac{1}{2}) \)
\(= \frac{3}{2} ⋅ \frac{1}{2} ⋅ π^{1/2} \) By property of Gamma function \(Γ(\frac{1}{2}) = π^{1/2} \)
\(= \frac{3}{4} . π^{1/2}. \)
5. Gamma function is defined as Γ(α) = 0∫∞ xα−1 e−x dx.
a) True
b) False
View Answer
Explanation: The Gamma function is defined as Γ(α) = 0∫∞ xα−1 e−x dx. Gamma function can also be defined as Γ(α+1) = αΓ(α).
6. Gamma distribution is Multi-variate distribution.
a) True
b) False
View Answer
Explanation: Gamma distribution is a uni-variate distribution that means it is only defined for x ranging from (0, ∞).
7. Which of the following graph represents gamma distribution?
a) 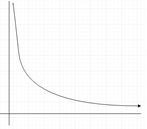
b) 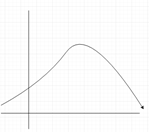
c) 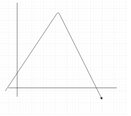
d) 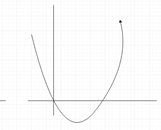
View Answer
Explanation: Gamma distribution is defined as
f(x) = λα xα−1 e−λx / Γ(α) for x > 0.
Hence it is an exponentially decreasing function.
Sanfoundry Global Education & Learning Series – Probability and Statistics.
To practice all areas of Probability and Statistics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Engineering Mathematics MCQ
- Apply for 1st Year Engineering Internship
- Practice Numerical Methods MCQ
- Check Probability and Statistics Books
