This set of Gas Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “Steady One-Dimensional Flow”.
1. The area-velocity relation for quasi one-dimensional flow through nozzle is given by _________
a) \(\frac {dA}{A} = -\frac {dV}{V}\)(1-M2)
b) \(\frac {dA}{A} = -\frac {dV}{V}\)(M2-1)
c) \(\frac {dV}{A} = -\frac {dA}{V}\)(1-M2)
d) \(\frac {dV}{A} = -\frac {dA}{V}\)(M2-1)
View Answer
Explanation: From continuity equation; ρAV = Constant.
Differentiating with respect to V: \(\frac {d(\rho AV)}{dV}\)=ρV\(\frac {dA}{V}\)+A\(\frac {d(\rho V)}{dV}\)=0
Where A \(\frac {d(\rho V)}{dV}\)=A(ρ+V\(\frac {dρ}{dp} \frac {dp}{dV}\))=Aρ(1-M2)
(Since from Bernoulli’s equation dp/dV=-ρV
And from Laplace equation dp/dρ=a2)
Hence \(\frac {dA}{A} = -\frac {dV}{V}\)(1-M2)
2. Define the speed of an object moving through air.
a) a=γRT
b) a=γ/RT2
c) a=\(\sqrt {\gamma RT}\)
d) a=γ/RT
View Answer
Explanation: For an adiabatic process equation of state is given by; P = ργRT
Differentiating it, dp = (γργ-1RT) dρs
dp/dρ = γp/ρ
And since for an isentropic process p = ρRT
dp/dρ = γRT
a = \(\sqrt {\gamma RT}\) (dp/dρ = a2)
3. Calculate the maximum velocity that can be obtained by expanding air at T0 = 288 K, into the vacuum.
a) 343.3 m/s
b) 649.2 m/s
c) 780.9 m/s
d) 760.6 m/s
View Answer
Explanation: The velocity of the air being discharged into the reservoir is given by;
V = \(\sqrt {(\frac {2γ}{γ-1})(\frac {p_0}{ρ_0 }) [ 1- (\frac {p_a}{p_0} )^{γ-1/γ} ] }\)
Now for discharge into vacuum Pa = 0, resulting into maximum velocity.
i.e. Vmax = \(\sqrt {(\frac {2γ}{γ-1}) (\frac {p_0}{ρ_0 }) }\)
Vmax = a0\(\sqrt {(\frac {2γ}{γ-1}) }\)
Vmax = 340.17\(\sqrt {(\frac {2}{1.4-1}) }\)
Vmax = 760.6 m/s
4. For the quasi one dimensional flow through the given convergent-divergent duct, which of the following is correct in direction of flow?
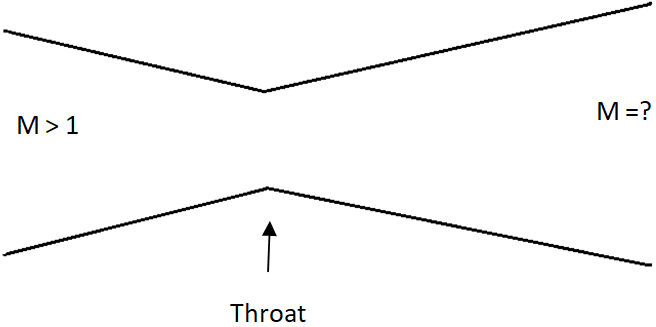
a) The static pressure increases and the Mach number decreases
b) Both the static pressure and Mach number Increases
c) The static pressure decreases and Mach number Increases
d) Both the static pressure and Mach number decreases
View Answer
Explanation: According to the area-velocity relation given by:
\(\frac {dA}{A}\) = (M2 – 1)\(\frac {du}{u}\)
for the diffuser having the supersonic flow i.e. M > 1, equation 1) becomes;
\(\frac {dA}{A} = \frac {du}{u}\)
Hence, from equation 2), as the supersonic flow passes through a convergent duct, the flow velocity decreases with a decrease in area and flow becomes subsonic i.e. M < 1. Thus equation 1) becomes
\(\frac {dA}{A} = \, – \frac {du}{u}\)
Hence as this subsonic flow passes through a divergent duct the velocity further decreases with an increase in area, and resulting into pressure rise.
5. For discharge of air through the reservoir into a vacuum, the air can be assumed as an incompressible medium.
a) True
b) False
View Answer
Explanation: For incompressible flow, from Bernoulli’s equation;
V = \(\sqrt {2(\frac { p_0-p}{ρ} )}\)
And for discharge into vacuum P = 0.
Vmax = \(\sqrt {2(\frac {p_0}{ρ_0} )}\) (ρ = ρ0 for incompressible flow)
Now for compressible flow Vmax = a0\(\sqrt {( \frac { 2}{\gamma – 1} )}\)
Hence from the above equations Vmax(comp.) = \(\sqrt {( \frac {\gamma }{\gamma – 1} )}\) Vmax(incomp.)
Vmax(comp.) = 1.9Vmax(incomp.)
Therefore, the air cannot be assumed as an incompressible medium.
6. For a quasi-one-dimensional subsonic flow through convergent duct, velocity of flow _________
a) Decreases
b) Increases
c) Remains constant
d) Become zero
View Answer
Explanation: As the quasi-one-dimensional subsonic flow passes through a convergent duct, its velocity increases in direction of flow. As by area-velocity relation for subsonic flow through a convergent duct
\(\frac {dA}{A}\) = (M2 – 1)\(\frac {dv}{v}\)
\(\frac {dA}{A} = \, – \frac {dv}{v}\)
Thus as the area of duct decreases the velocity of a supersonic flow also increases, resulting in a decrease in static pressure of the flow.
7. Calculate the Mach number for an aircraft flying at 530 m/s and at an altitude of 5 Km from sea level at temperature 255.7 K.
a) 1.65
b) 1.67
c) 1.72
d) 1.79
View Answer
Explanation: The Mach number can be obtained by; M = V/a
Where, V = 530 m/s
And, a = \(\sqrt {γRT} = \sqrt {1.4*287*255.7}\) = 320.53 m/s
Hence, M = 530/320.53 = 1.65
8. What will be the value of the characteristics Mach number for air if the local Mach number tends to reach infinity?
a) 1
b) 1.37
c) 2.45
d) Infinite
View Answer
Explanation: The relation between characteristics Mach number and local Mach number is;
M2=\(\frac {2}{((γ+1/M^{*2} )-(γ-1) )}\)
Now at M → ∞, M* → \(\sqrt {\frac {γ+1}{γ-1}}\) → 2.45 (As for air, γ = 1.4)
9. For the calorically perfect gas, the speed of sound is dependent on the temperature only.
a) True
b) False
View Answer
Explanation: For the calorically perfect gas, the specific heats Cp and Cv are independent of temperature,
Cv ≠ f (T) and Cp ≠ f (T)
And the ratio of specific heats (γ) is also constant.
Now since the speed of sound is given by; a=\(\sqrt {γRT}\)
We can say that for the calorically perfect gas, the speed of sound is dependent on temperature only.
10. Determine the value of the critical density ratio for air at sea level condition.
a) 0.913
b) 0.528
c) 0.833
d) 0.634
View Answer
Explanation: From the isentropic flow relations;
\(( \frac {ρ^*}{ρ_0} )=(\frac {T^*}{T_0} )\)1/(γ-1)
\(( \frac {ρ^*}{ρ_0} ) = [1+( \frac {γ-1}{2}) \)M2]1/(γ-1)
\(( \frac {ρ^*}{ρ_0} )=[ ( \frac {2}{γ+1} ) ]\)1/(γ-1) (at M*, M=1)
\(( \frac {ρ^*}{ρ_0} )\) = 0.634 (γ=1.4)
Sanfoundry Global Education & Learning Series – Gas Dynamics.
To practice all areas of Gas Dynamics, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
