This set of Gas Dynamics Multiple Choice Questions & Answers (MCQs) focuses on “De Laval Nozzle – Set 2”.
1. Which of the following curve represents the choked condition inside the nozzle?
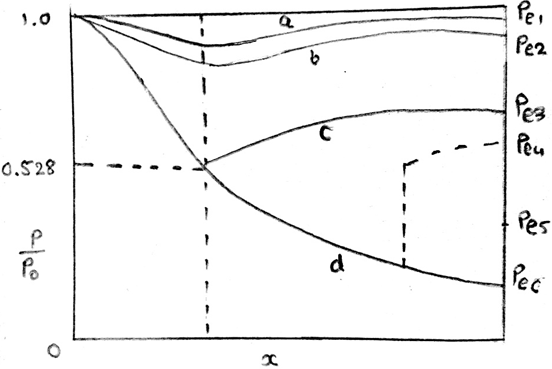
a) a
b) b
c) c
d) ds
View Answer
Explanation: When the nozzle exit pressure is reduced such that the flow reaches the sonic velocity at throat i.e. M = 1, the mass flow remains constant even with a further decrease in exit pressure. Such condition is called choked flow and for C-D nozzle the maximum mass flow rate occurs at Pe/P0 = 0.528. Hence the curve ‘c’ represents the choked condition inside the nozzle.
2. At which condition the normal shock wave occurs at some distance downstream of the throat?
a) Pb < Pe < Pth
b) Pb > Pe > Pth
c) Pb = Pe = Pth
d) Pb = 0
View Answer
Explanation: When the nozzle exit pressure is further decreased below Pth the flow becomes supersonic creating a normal shock wave at downstream of the throat. This results in the subsonic flow behind the shock and it further slows down as it moves to exit.
3. The nozzle is said to be over expanded when __________
a) Pe > Pb
b) Pe = Pb
c) Pe < Pb
d) Pe = Pth
View Answer
Explanation: A nozzle is said to be over expanded when Pe < Pb, as at Pe < Pb, the back pressure is still above the isentropic pressure at the nozzle exit. Hence the flow inside the nozzle must increase its pressure to be equal to back pressure. For this compression takes place across an oblique shock wave at nozzle exit such that Pe = Pb.
4. What flow phenomenon occurs inside the nozzle when the exit pressure is greater than the back pressure?
a) Over-expansion
b) Under expansion
c) Isentropic expansion
d) Isentropic compression
View Answer
Explanation: When the nozzle exit pressure is greater than back pressure i.e. Pe > Pb, the nozzle exit pressure needs to be reduced to match with back pressure. Hence the flow expands through centered expansion fan to decrease the pressure so that Pe = Pb. And this flow phenomenon is called under expansion.
5. Among the following which one has the subsonic flow at the throat and the divergent portion acts as a diffuser?
a) C-D nozzle
b) Orifice
c) Pitot tube
d) Venturi
View Answer
Explanation: In the venture, the pressure gradient is not quite high enough for the flow to accelerate with high velocity inside the nozzle. Hence the flow remains subsonic at the throat and due to this according to area-velocity relation as the flow moves through divergent duct it further slows down since the divergent portion now acts as a diffuser.
6. For a given De Laval nozzle there is only one exit Mach number that can be produced.
a) True
b) False
View Answer
Explanation: We know that the area-Mach number relation is given by;
\((\frac {A}{A^*} )^2=\frac {1}{M^2} [ \frac {2}{γ+1} ( 1+\frac {γ-1}{2} M^2 ) ] \)(γ+1)/(γ-1)
Now, considering an air at standard sea level condition i.e. γ = 1.4,
\((\frac {A}{A^*} ) = \frac {1}{M} [ \frac {5+ M^2}{6}] \)3
Hence from the above equation, it is seen that for a given De Laval nozzle having a required exit Mach number, there is only one ratio of exit area to throat area i.e. for a given De Laval nozzle, there is only one Mach number that can be produced.
7. At which condition the De Laval nozzle produces maximum thrust?
a) Pe = Pb
b) Pe < Pb
c) Pe > Pb
d) Pe = 0
View Answer
Explanation: The general thrust equation for a De Laval nozzle is;
T = \(\dot{m}\)Ve + (Pe – Pb) Ae
Now at Pe = Pb, T = \(\dot{m}\)Ve
Thus when the nozzle exit pressure is equal to the back pressure or atmospheric pressure, the nozzle produces maximum thrust.
8. In a C-D nozzle where exit pressure is equal to back pressure i.e. Pe = Pb, refers to which type of flow?
a) Over-expansion
b) Under expansion
c) Isentropic expansion
d) Isentropic compression
View Answer
Explanation: When Pe = Pb, there is no discontinuity of pressure in relation to the surrounding. Hence the flow exits the nozzle and into surrounding smoothly without passing through any shock waves. Hence such type of flow is called isentropic expanded flow.
9. If the air at stagnation pressure 5 bar and temperature 400 K is discharged through the isentropic De Laval nozzle and expands to surrounding at sea level condition. Calculate the isentropic discharge speed.
a) 343.33 m/s
b) 492.65 m/s
c) 544.26 m/s
d) 637.81 m/s
View Answer
Explanation: For a flow through nozzle maximum discharge speed is expressed by;
Ve = \(\sqrt {\frac {2γRT}{γ-1} [1-(\frac {P_e}{P_0} )^{(γ-1)/γ} ] } \)
For air at sea level condition Pe = 1 bar,
Therefore, Ve = \(\sqrt {\frac {2*1.4*287*400}{1.4-1} [1-(\frac {1}{5})^{(1.4-1)/1.4} ] }\)
Ve = 544.26 m/s
10. Define kinetic energy efficiency for a nozzle.
a) ηn = (Ve/V’e)
b) ηn = (Ve/V’e)2
c) ηn = (V’e/Ve)
d) ηn = (V’e/Ve)2
View Answer
Explanation: The kinetic energy efficiency for a nozzle is defined as, “The square of the ratio of the actual velocity (Ve) of the gases crossing the nozzle exit area Ae to the corresponding isentropic velocity of gases (V’e).
That is; ηn = (Ve/V’e)2
11. The gas stored in the reservoir having pressure 7 bar and temperature 300 K exhausts from the nozzle which has an exit area of 0.025 m2 to surroundings at velocity 570 m/s. The mass flow rate through the nozzle is 23 Kg/s and surrounding having pressure of 1 bar. Calculate the thrust produced by the nozzle.
a) 26.45 KN
b) 33.69 KN
c) 28.11 KN
d) 18.83 KN
View Answer
Explanation: The nozzle thrust equation is defined as;
T = \(\dot{m}\)Ve + (Pe – Pb) Ae
Now, Me = Ve/a = 1.67
Where a = \(\sqrt {γRT} = \sqrt {1.4*287*288}\) = 340.17 m/s
Thus, Ve = Me*a = 1.67*340.17 = 568 m/s
And T = 23*568+(7*105-1*105)*0.025
T = 28.11 KN
12. The nozzles having different divergence angle are listed below. Among the mentioned cases which nozzle will produce the maximum thrust?
a) 3°
b) 9°
c) 7°
d) 11°
View Answer
Explanation: To take into account the losses due to the radial divergence of the streamlines, the one-dimensional thrust is corrected by;
F = λ*Fs
Where Fs is one-dimensional thrust
And λ is divergence factor = (1+cosα)/2
Therefore as the divergence angle increases the divergence factor decreases, in turn decreasing the nozzle thrust. Hence the maximum thrust is produced by minimum divergence angle.
13. In which of the following case the flow separation occurs in the De Laval nozzle?
a) Under expansion
b) Over expansion
c) Isentropic compression
d) Isentropic expansion
View Answer
Explanation: In an overexpansion condition the nozzle exit pressure is much lower than the back pressure i.e. Pe < Pb. Now due to this, the boundary layer flows in direction of positive pressure gradient and the momentum is removed from the boundary layer faster then it receives the movement from the mainstream. This causes the flow to detach from boundary layer resulting in flow separation.
14. For which of the following exit pressure the nozzle will not choke when the fluid expands through a nozzle into the atmosphere at 2.6 bar.
a) 4.8 bar
b) 5.1 bar
c) 6.7 bar
d) 7.4 bar
View Answer
Explanation: The nozzle chocks when the ratio of back pressure to nozzle exit pressure is less than or equal to 0.528, i.e. P0/Pe ≤ 0.528. Now among the above four cases only for Pe = 4.8 bar, P0/Pe > 0.528. Hence the nozzle will not choke for such case.
15. Calculate the mass flow rate for a nozzle having throat area 0.6 m2 and having stagnation pressure and temperature 12 bar and 850 K respectively. Take the air as a fluid.
a) 583.23 Kg/s
b) 649.84 Kg/s
c) 836.51 Kg/s
d) 998.16 Kg/s
View Answer
Explanation: The mass flow rate through the nozzle is defined by;
\(\dot{m} = \frac {p_0 A^*}{\sqrt {T_0 } } \sqrt { \frac {γ}{R} \frac {2}{γ+1}^{(γ+1)/(γ-1)} } \)
Now for air γ = 1.4 and R = 287 J/Kg*K
Hence, for given flow properties \(\dot{m} = \frac {12*10^5*0.6}{\sqrt {850}}\sqrt {\frac {1.4}{287} ( \frac {2}{1.4+1}^{(1.4+1)/(1.4-1)} )}\)
\(\dot{m}\) = 998.16 Kg/s
Sanfoundry Global Education & Learning Series – Gas Dynamics.
To practice all areas of Gas Dynamics, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
