This set of Multiple Choice Questions & Answers (MCQs) focuses on “Robotics – Set 4”.
1. What refers to changing the description of a point (or vector) in space from one frame to another frame?
a) Mapping
b) Rotation
c) Shifting
d) Translation
View Answer
Explanation: Mapping refers to changing the description of a point in space from one frame to another frame. One frame with respect to another has three possibilities such as changing orientation, translation and both.
2. What is referred as the rotation of the second frame with respect to the first while the origin of both the frame is same?
a) Changing the orientation
b) Translation of the origin
c) Shifting
d) Mapping
View Answer
Explanation: Changing of origin refers to the rotation of one axis about another axis such that the origin of both of them remain same. It can be simply called as rotation but in robotics it is termed as changing the orientation.
3. The columns (and therefore the rows) of rotational matrix R are mutually orthogonal. True or False?
a) True
b) False
View Answer
Explanation: Rotation matrices are square matrices and they can be characterized as orthogonal matrices with determinant 1. Alternatively it can be said that a square matrix R is a rotation matrix if and only if RT = R−1 and det R = 1.
4. R being a rotational matrix, inverse of R = Transpose of R. True or False?
a) True
b) False
View Answer
Explanation: To provide geometric intuition for the notion of the inverse of a rotation matrix, let us consider a two dimensional case, the inverse of the rotation matrix corresponding to a rotation by angle θ can also be easily computed simply by constructing the rotation matrix for a rotation by the angle −θ:
\(\begin{bmatrix}
cos(-θ) & -sin(-θ) \\
sin(-θ) & cos(- θ) \\
\end{bmatrix} =
\begin{bmatrix}
cosθ & sinθ \\
-sinθ & cosθ \\
\end{bmatrix} =
\begin{bmatrix}
cosθ & -sinθ \\
sinθ & cosθ \\
\end{bmatrix}\)T
5. For every n×n rotation matrix R (for n = 2, 3), each column (and therefore each row) of R is which vector?
a) Unit
b) Unique
c) Zero
d) Undefined
View Answer
Explanation: Every rotation matrix has columns and row as unit vectors as we can see from the basic expression of rotation matrix with two principal axes as XYZ and UVW and U, V, W, X, Y, Z are unit vectors.
R = \(\begin{pmatrix}
U.X & U.Y & U.Z \\
V.X & V.Y & V.Z \\
W.X & W.Y & W.Z \\
\end{pmatrix}\)
6) For a 2×2 rotation matrix R, det{R} = 0, True or False?
a) True
b) False
View Answer
Explanation: Using the definition of a determinant we can see that the determinant of a rotation matrix is equal to 1. It is clear that the geometric interpretation would be that the area does not change. Det(R), = \(\begin{bmatrix}
cosθ & sinθ \\
-sinθ & cosθ \\
\end{bmatrix}\) = 1
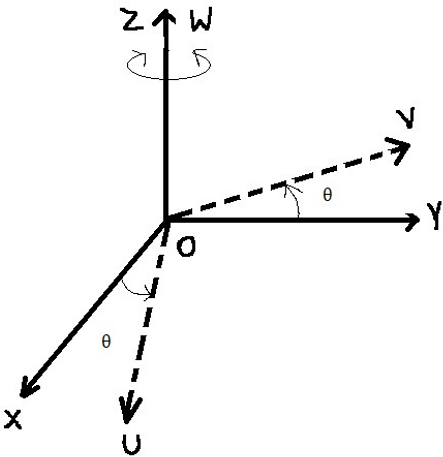
7) Which of the following denotes the rotation of frame {2} with respect to frame {1} by an angle θ about the z axis of frame {1}?
a) Rz(θ) = \(\begin{pmatrix}
1 & 0 & 0 \\
0 & cosθ & -sinθ \\
0 & sinθ & cosθ \\
\end{pmatrix}\)
b) Rz(θ) = \(\begin{pmatrix}
cosθ & 0 & sinθ \\
0 & 1 & 0 \\
-sinθ & 0 & cosθ \\
\end{pmatrix}\)
c) Rz(θ) = \(\begin{pmatrix}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{pmatrix}\)
d) Undefined
View Answer
Explanation: Rz(θ) is computed from dot product of unit vectors along the principle axes. Thus,
Rz(θ) = \(\begin{pmatrix}
cosθ & -cos(90+θ) & cos90 \\
cos(90-θ) & cosθ & cos90 \\
cos90 & cos90 & cos0
\end{pmatrix}\)
= Rz(θ) = \(\begin{pmatrix}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{pmatrix}\)
8. Consider two frames {1} and frame {2}, with origins O1 and O2 such that axes of frames {1} are parallel to axes of frame {2}. A point P in space can be expressed as vectors O1P and O2P and the distance between then is O1O2, then which of the following is true?
a) O1P = O2P + O1O2
b) O1P = O2P * O1O2
c) O1P = O2P / O1O2
d) O1P = O2P – O1O2
View Answer
Explanation: The correct way of notation is O1P = O2P + O1O2. This can be interpreted considering a three dimensional figure with two frames {1} and {2} such that the origins are parallel. If the origin of the two frames are parallel then there should be some distance O1O2 between the two frames. So point P in space can be expressed according to distance notation between the frames as O1P = O2P + O1O2.
9. Which of the following denotes the rotation of frame {2} with respect to frame {1} by an angle θ about the x axis of frame {1}?
a) Rx(θ) = \(\begin{pmatrix}
1 & 0 & 0 \\
0 & cosθ & -sinθ \\
0 & sinθ & cosθ \\
\end{pmatrix}\)
b) Rx(θ) = \(\begin{pmatrix}
cosθ & 0 & sinθ \\
0 & 1 & 0 \\
-sinθ & 0 & cosθ \\
\end{pmatrix}\)
c) Rx(θ) = \(\begin{pmatrix}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{pmatrix}\)
d) Undefined
View Answer
Explanation: Rx(θ) is computed from dot product of unit vectors along the principle axes. Thus,
Rx(θ) = \(\begin{pmatrix}
cos0 & cos90 & cos90 \\
cos90 & cosθ & -cos (90+θ) \\
cos90 & cos (90+θ) & cosθ \\
\end{pmatrix}\)
= Rx(θ) = \(\begin{pmatrix}
1 & 0 & 0 \\
0 & cosθ & -sinθ \\
0 & sinθ & cosθ \\
\end{pmatrix}\)
10. Which of the following denotes the rotation of frame {2} with respect to frame {1} by an angle θ about the y axis of frame {1}?
a) Ry(θ) = \(\begin{pmatrix}
1 & 0 & 0 \\
0 & cosθ & -sinθ \\
0 & sinθ & cosθ \\
\end{pmatrix}\)
b) Ry(θ) = \(\begin{pmatrix}
cosθ & 0 & sinθ \\
0 & 1 & 0 \\
-sinθ & 0 & cosθ \\
\end{pmatrix}\)
c) Ry(θ) = \(\begin{pmatrix}
cosθ & -sinθ & 0 \\
sinθ & cosθ & 0 \\
0 & 0 & 1 \\
\end{pmatrix}\)
d) Undefined
View Answer
Explanation: Ry(θ) is computed from dot product of unit vectors along the principle axes. Thus,
Ry(θ) = \(\begin{pmatrix}
cosθ & cos90 & cos (90-θ) \\
cos90 & cos0 & cos90 \\
-cos (90+θ) & cos90 & cosθ \\
\end{pmatrix}\)
= Ry(θ) = \(\begin{pmatrix}
cosθ & 0 & sinθ \\
0 & 1 & 0 \\
-sinθ & 0 & cosθ \\
\end{pmatrix}\)
Sanfoundry Global Education & Learning Series – Robotics.
To practice all areas of Robotics, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
