This set of Multiple Choice Questions & Answers (MCQs) focuses on “Robotics – Set 7”.
1. Which models gives relation between the position and orientation of the end-effector and spatial positions of joint-links?
a) Kinematic model
b) Differential model
c) Integral model
d) Static model
View Answer
Explanation: Kinematic model is used to for spatial description of robotic manipulators. It is used to find the position and orientation of the end-effector when spatial positions of joint-links are known and vice-versa. Kinematic model is divided into Direct kinematic model and Indirect kinematic model.
2. Which kinematic model deals with a given set of joint-link parameter, to find the position and orientation of the end-effector with respect to the known reference frame?
a) Direct Kinematic model
b) Differential model
c) Integral model
d) Inverse Kinematic model
View Answer
Explanation: Direct Kinematic model gives the position and orientation of the end-effector as a function of the joint variables and other joint-link constant parameters. Direct Kinematic model is also called as Forward kinematics or Direct kinematics.
3. Which kinematic model deals with a given position and orientation of the end-effector with respect to the inertial reference frame to find the required set of joint variables to bring the end-effector to the specified position and orientation?
a) Direct Kinematic model
b) Differential model
c) Integral model
d) Inverse Kinematic model
View Answer
Explanation: Inverse Kinematic model gives the required set of joint variables to bring the end-effector to the specified position and orientation. The problem of inverse kinematics is more difficult than the forward kinematics problem.
4. Which of the following is not present in an open loop system?
a) Plot
b) Input
c) Output
d) Feedback
View Answer
Explanation: Feedback mechanism is not present in an open loop system because an open loop control system acts completely on the basis of input and the output has no effect on the control action that is feedback mechanism is not present. Whereas in a closed loop control system the current output alters the action to fit desired condition that means feedback mechanism is present.
5. If J(q) is the Jacobian of a manipulator, Ve is the end effector velocity and vector ǭ is the joint velocities, then which of the following equations are correct?
a) Ve =J(q)* ǭ
b) Ve – J(q) = ǭ
c) Ve + J(q) = ǭ
d) Ve * J(q) = ǭ
View Answer
Explanation: If J(q) is the Jacobian of a manipulator, Ve is the end effector velocity and vector ǭ is the joint velocities then the correct equation is Ve =J(q)* ǭ. Manipulator Jacobian gives the relation between Cartesian velocities of end effector to linear velocities.
6. Which of the following refers to the differential motion of manipulators?
a) Direct Kinematic model
b) Differential model
c) Integral model
d) Inverse Kinematic model
View Answer
Explanation: Differential kinematics of a manipulator refers to differential motion, that is, velocity, acceleration, and all higher order derivatives of position variables. This is also known as Dynamic modelling and some of the methods include Lagrangian-Euler formulation and Netwon formulation.
7. Which of the following denote Denavit-Hartenberg representation of transformation matrix?
(cosθ =cθ , sinθ =sθ, cosα =cα , sinα =sα for link i ; a, d translation along x and z axes and θ ,α are rotation about z and x axes respectively)
a) i-1Ti = \(\begin{bmatrix}
cθ & -sθ cα & sθ sα & acθ\\
sθ & cα cθ & -cθ sα & asθ\\
0 & sα & cα & d\\
0 & 0 & 0 & 1
\end{bmatrix}\)
b) i-1Ti = \(\begin{bmatrix}
sθ & -sθ cα & sθ sα & acθ\\
cθ & cα cθ & -cθ sα & asθ\\
0 & sα & cα & d\\
0 & 0 & 0 & 1
\end{bmatrix}\)
c) i-1Ti = \(\begin{bmatrix}
cθ & -sθ & sα & acθ\\
sθ & cθ & -sα & asθ\\
0 & sα & cα & d\\
0 & 0 & 0 & 1
\end{bmatrix}\)
d) i-1Ti = \(\begin{bmatrix}
cθ & -sθ cα & sθ sα & acθ\\
sθ & cα cθ & cθ sα & asθ\\
1 & sα & cα & d\\
0 & 0 & 0 & 1
\end{bmatrix}\)
View Answer
Explanation: Denavit-Hartenberg representation of transformation matrix is obtained from
i-1Ti = TZ (θi) TZ (di) TX(ai) TX(αi)
i-1Ti = \(\begin{bmatrix}
cθ & -sθ & 0 & 0\\
sθ & cθ & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & d\\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & 0 & a\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & 0 & 0\\
0 & cα & -sα & 0\\
0 & sα & cα & 0\\
0 & 0 & 0 & 1
\end{bmatrix}\) = \(\begin{bmatrix}
cθ & -sθ cα & sθ sα & acθ\\
sθ & cα cθ & -cθ sα & asθ\\
0 & sα & cα & d\\
0 & 0 & 0 & 1
\end{bmatrix}\)
8. How many DH (Denavit-Hartenberg) parameters exist for any manipulator?
a) 2
b) 3
c) 4
d) 6
View Answer
Explanation: Four DH (Denavit-Hartenberg) parameters exist for any manipulator.The four DH parameters ai, αi, di, and θi which indicate link length, link twist, link offset, and joint angle, respectively. In other terms a, d are translation along x and z axes and θ ,α are rotation about z and x axes respectively.
9. Which of the following are the DH parameters of 2-DOF planar manipulator shown below?
(One revolute joint {1} and one prismatic joint {2}) and (ai, di translation along x and z axes and θi, αi are rotation about z and x axes respectively)
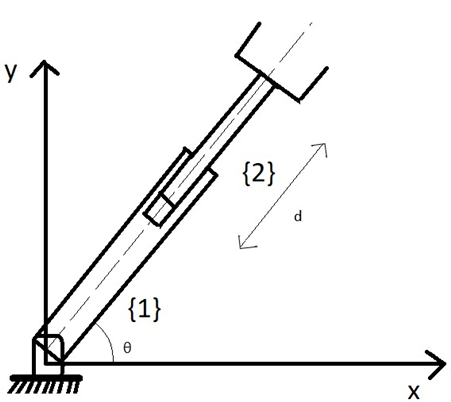
a)
| link | ai | αi | di | θi |
|---|---|---|---|---|
| {1} | 0 | 900 | 0 | θ |
| {2} | 0 | 0 | d | 0 |
b)
| link | ai | αi | di | θi |
|---|---|---|---|---|
| {1} | 0 | 0 | 0 | 900 |
| {2} | 0 | θ | d | 0 |
c)
| link | ai | αi | di | θi |
|---|---|---|---|---|
| {1} | 0 | 900 | d | 900 |
| {2} | 0 | θ | 0 | 0 |
d)
| link | ai | αi | di | θi |
|---|---|---|---|---|
| {1} | 0 | 0 | 0 | 0 |
| {2} | 0 | 1800 | d | θ |
Explanation: To find out the DH parameters we have to first draw the free body diagram for the manipulator. While drawing free body diagram we should make sure that xi should always intersect and be perpendicular to xi-1. We should also define motion direction along z.

Now, as we know ai, di are translation along x and z axes and θi, αi are rotation about z and x axes respectively we can write the DH parameters as
| link | ai | αi | di | θi |
|---|---|---|---|---|
| {1} | 0 | 900 | 0 | θ |
| {2} | 0 | 0 | d | 0 |
10. Inverse Kinematic problem is more complex to solve than Direct Kinematic problem. True or False?
a) True
b) False
View Answer
Explanation: Inverse Kinematic problem is more complex to solve than Direct Kinematic problem because Inverse Kinematics involve nonlinear simultaneous equations, involving transcendental functions. The number of simultaneous equations is generally more than number of unknowns, so it leads to a problem of multiple solutions or non-existence of any solution.
Sanfoundry Global Education & Learning Series – Robotics.
To practice all areas of Robotics, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
