Theory of Computation – Language of a DFA and Extended Transition Function

Language of a Deterministic Finite Automaton
A DFA defines a language. The set of all strings that result in a sequence of state transition from start state to an accepting state is the language defined by the DFA. The language is denoted as L(M) for a DFA M = (Q, Σ, δ, F q₀), and is defined by

Extended transition function
An extended transition function takes two arguments. The first argument is a state q and the second argument is a string w. It returns a state just like the transition function discussed in the previous tutorials. It can be defined as the state in which the FA ends up, if it begins in state q and receives string x of input symbols.
We define δ* recursively as follows:

1. For any q ϵ Q, δ*(q, є) = q

2. For any q ϵ Q and a ϵ Σ,
   δ*(q, ya) = δ(δ*(q,y), a)

For a string of length 1 δ*(q, a) = δ(q, a).

Question: Design a DFA for the language L = {w ϵ (a,b)*: n_b mod 3 > 1}.
View Answer

Answer: n_b represents the number of b in the string. n_b mod 3 gives the remainder when n_b is divided by 3. n_b mod 3 > 1 implies that the remainder is 2. That means the number of b can be 2, 5, 8, …
Let M = (Q, Σ, δ, F q₀) be the DFA
Σ = {a, b} is given.

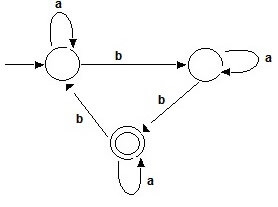
For the automaton
Q = {q₀, q₁, q₂}
F = {q₂}

Question on designing and programming a DFA have been covered in the next tutorial.

Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.

If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.