This set of Astronautics Multiple Choice Questions & Answers (MCQs) focuses on “Real Orbits – Gravity Anomalies”.
1. The regression of nodes causes _______________
a) an out-of-plane precession
b) an in-plane precession
c) a change in orbital eccentricity
d) a change in orbital size
View Answer
Explanation: Nodal regression is similar to gyroscopic precession and happens only for inclined orbits. Let us assume that the orbital torque vector, which is a vector perpendicular to the orbit and passing through its center, as ‘O’. Now when the satellite is at its highest point in the orbit, it is pulled vertically downwards due to the extra mass at the equator. At the lowest point in the orbit, it is similarly pulled vertically upwards again due to additional equatorial mass. This creates a torque ‘T’ that points along the line of nodes, as shown in the illustration below:
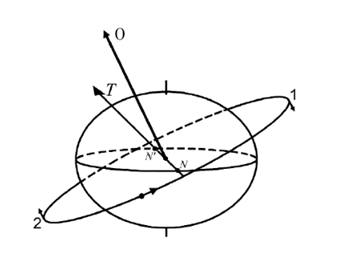
Similar to gyroscopic precession, the orbital vector ‘O’ now tends to align itself with ‘T’, causing a precession of the orbital plane.
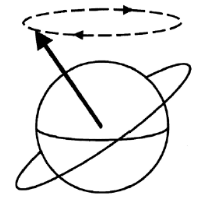
The result is that the entire orbit itself undergoes an out-of-plane rotation, illustrated in the following diagram:
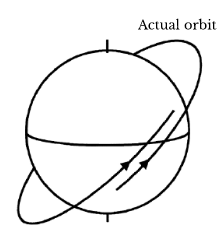
2. Regression of nodes occurs only for _______________
a) polar orbits
b) equatorial orbits
c) geostationary orbits
d) orbits with non-zero and non-polar inclinations
View Answer
Explanation: Polar inclinations cannot develop out-of-plane forces at the highest and lowest points of the orbit (due to the symmetry of gravitational forces at these points), while equatorial orbits lie in the plane of the equator itself. The absence of any resulting torque means that the orbit cannot experience any sort of precession.
3. Circular orbits do not undergo nodal regression.
a) True
b) False
View Answer
Explanation: If the circular orbit has a finite but non-polar inclination, it can very much experience out-of-plane forces at the northernmost and southernmost points of the orbit (due to the extra mass at the equator) and hence undergo nodal regression. The reason for the name for this anomaly is because the line of nodes (line joining the ascending and descending nodes) appears to rotate about the center of the Earth in the equatorial plane itself.
4. Which of the following parameters varies in the case of nodal regression?
a) orbital radius
b) semi-major axis
c) eccentricity
d) right ascension of ascending node
View Answer
Explanation: Since an orbit undergoing nodal regression precesses about Earth’s rotational axis, the nodes of the orbit keep on shifting, causing the ascending node (and the descending node too) to change position with time. This, by default, is accompanied by a change in the right ascension of the orbit. As a rule of thumb, the ascending node moves west for prograde orbits and east for retrograde orbits.
5. Polar orbits experience only perigee precession.
a) True
b) False
View Answer
Explanation: Polar orbits can only undergo apsidal precession (in case they are elliptical). Nodal regression is not possible because the extra gravitational pull from Earth’s equatorial bulge is balanced equally from all possible directions at the highest and lowest orbital locations, preventing the formation of a couple.
6. In nodal regression, which of the following parameters remains unchanged?
a) longitude of perigee
b) argument of perigee
c) right ascension of ascending node
d) orientation of the line of nodes
View Answer
Explanation: Nodal regression occurs in such a way that the right ascension (along with the line of nodes by default) and the perigee (in case of elliptical orbits) keep shifting while the orbit precesses. The longitude of perigee is measured from a reference direction and is hence a variable parameter. The same is true for the right ascension. The argument of perigee, however, is fixed because this orbital element is measured with reference to the ascending node. Both the ascending node and perigee point continuously drift in equal amounts, thereby maintaining the same angle between the ascending node and perigee as the original.
7. Which of the following statements are true?
a) Nodal regression is less for higher altitudes while perigee precession is less for lower altitudes.
b) Nodal regression is greater for higher altitudes while perigee precession is greater for lower altitudes
c) Perigee precession and nodal regression are less for higher altitudes.
d) Perigee precession and nodal regression are more for higher altitudes.
View Answer
Explanation: Both the mentioned effects are due to the non-spherical Earth. As the satellite goes higher and higher, Earth appears more and more uniform and spherical, meaning that these anomalies are much less in magnitude at greater orbital heights.
8. An elliptical orbit undergoes perigee precession at a rate of around 11 degrees per day. How long does it take for the argument of perigee to shift by 90 degrees?
a) 11 days
b) 90 days
c) 91.1 days
d) 8.18 days
View Answer
Explanation: The time taken for the perigee to shift by 90 degrees = (90 degrees)/(11 degrees/day) = 8.18 days.
9. A circular orbit of time period 120 minutes undergoes nodal regression at a rate of 5 degrees per day. By how many degrees does the orbit shift in one rotation?
a) 0.6 degrees
b) 0.4 degrees
c) 0.64 degrees
d) 6.4 degrees
View Answer
Explanation: Number of orbits per day = (1440 minutes per day)/(120 minutes per orbit) = 12 orbits per day. Given, the orbit shifts by a total of 5 degrees in a day. So in one rotation, the orbits shifts by ((5 degrees)⁄day)/((12 orbits)/day) degrees, or 0.4 degrees per orbit.
10. A circular orbit of height 300 km regresses at a rate of 7 degrees per day. By how much does the orbit regress in just one rotation? (Assume the mass of Earth as 5.972 × 1024 kg and its radius as 6378 km)
a) 0.7˚
b) 0.44˚
c) 7˚
d) 0.74˚
View Answer
Explanation: We first need to find the time period of the orbit using the following equation:
T2 = \(\frac{4π^2}{GM}r^3\)
Given, r = (6378 + 300) x 103 meters = 6678000 m. M = 5.972 × 1024 kg.
Therefore, we get T = 5431.19 seconds = 90 minutes = 1.5 hours.
Number of orbits in a day = (24 hours)/((1.5 hours)⁄orbit)= 15.9 orbits per day. Now, we have a regression of 7 degrees per day. So the amount of deviation for just one orbit is ((7 degrees)⁄day)/((15.9 orbits)⁄day)= 0.44 degrees per orbit.
Sanfoundry Global Education & Learning Series – Astronautics.
To practice all areas of Astronautics, here is complete set of Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
