Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structure. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key'[1]), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
It uses the opposite strategy as depth-first search, which instead explores the node branch as far as possible before being forced to backtrack and expand other nodes.
Write a C program which will print the BFS traversal of a graph.
1. Start with the initial node.
2. Mark the initial node as visited and enqueue it.
3. While the queue is not empty:
- Dequeue a node from the queue.
- If the dequeued node is the goal node, stop the search.
- Otherwise, enqueue any successors (nodes that are directly connected to the dequeued node) that have not yet been visited.
4. If the queue is empty, every node on the graph has been visited, or there is no path from the initial node to the goal node.
5. If the goal node was found, return the path that was followed.
There are many ways to create a program in C which will print the BFS traversal of a graph. The following are the methods to print the BFS traversal of a graph.
- BFS Program in C using Adjacency Matrix
- BFS Program in C using Adjacency List
- BFS Program in C using Queue
Consider the following graph:
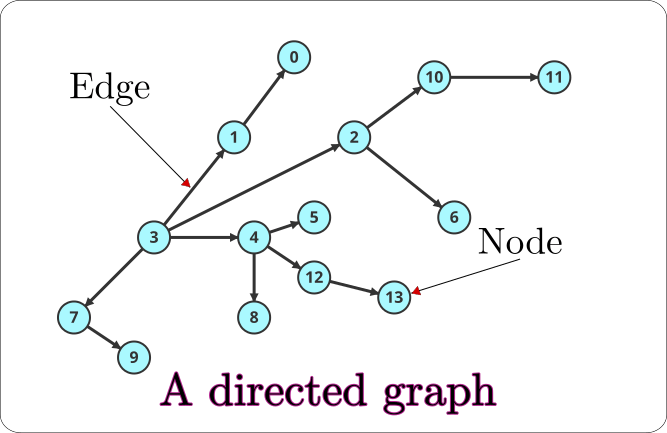
Step 1:
Start from source s = 3.
Set Q = {3}.
Q is the queue of nodes to visit.
3 being the only node in the queue, we visit it.
We mark 3 as visited and enqueue its unvisited neighbors 1, 2, 4, 7.
Step 2:
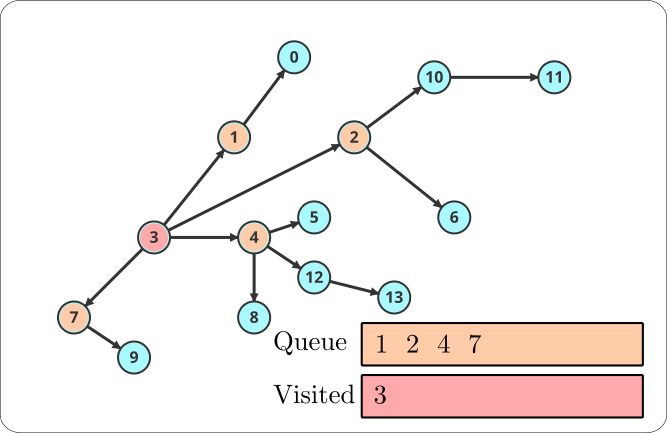
Q is now {1, 2, 4, 7} while V is {3}.
We dequeue 1 and visit it. 0 is its only unvisited neighbor, so we mark 1 as visited and enqueue 0.
We then dequeue 2 and visit it. 10 and 6 are its unvisited neighbors, so we mark 2 as visited and enqueue 6 and 10.
Similarly, we mark 4 as visited and enqueue 5, 12, and 8 and mark 7 as visited and enqueue 9.
Step 3:
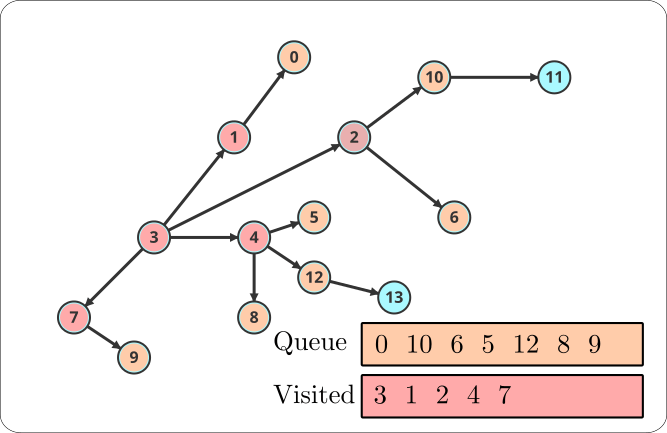
Q is now {0, 10, 6, 5, 12, 8, 9} while V is {3, 1, 2, 4, 7}.
We dequeue 0 and visit it. There are no unvisited neighbors, so we mark 0 as visited.
Similarly, we mark 10 as visited and enqueue 11 and mark 6 as visited. We then dequeue 5 and visit it. There are no unvisited neighbors, so we mark 5 as visited. Same goes for 12 and 8. For 12 we enqueue 13. We then dequeue 9 and visit it.
Step 4:
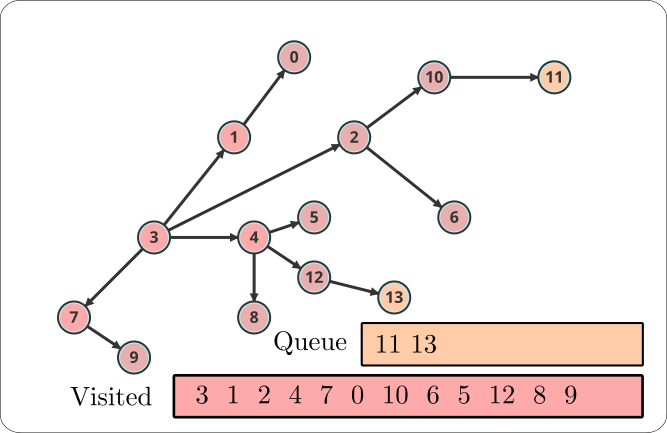
Q is now {11, 13} while V is {3, 1, 2, 4, 7, 0, 10, 6, 5, 12, 8, 9}.
We dequeue 11 and visit it. There are no unvisited neighbors, so we mark 11 as visited. We then dequeue 13 and visit it.
Step 5:
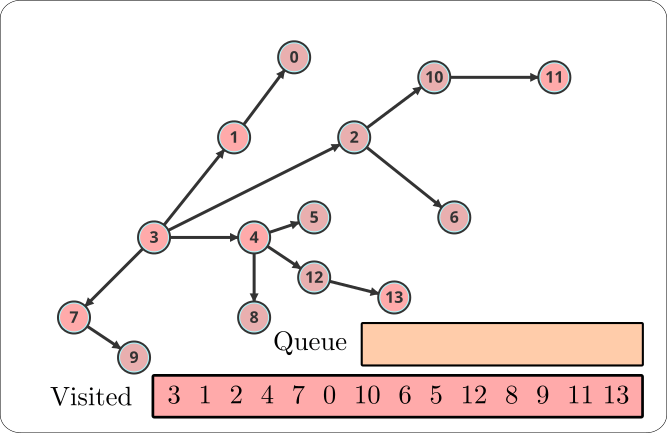
Awesome! We have visited all the nodes in the graph. The queue is now empty, so we stop the search. The BFS traversal of the graph is 3, 1, 2, 4, 7, 0, 10, 6, 5, 12, 8, 9, 11, 13.
In this approach, we will use a 2D array to represent the graph. The array will have the size of n x n where n is the number of nodes in the graph. The value of the array at index [i][j] will be 1 if there is an edge between node i and node j and 0 otherwise.
Here is source code of the C program to implement bfs using adjacency matrix. The C program is successfully compiled and run on a Linux system. The program output is also shown below.
/* * C program to implement bfs using adjacency matrix */ #include <stdio.h> int n, i, j, visited[10], queue[10], front = -1, rear = -1; int adj[10][10]; void bfs(int v) { for (i = 1; i <= n; i++) if (adj[v][i] && !visited[i]) queue[++rear] = i; if (front <= rear) { visited[queue[front]] = 1; bfs(queue[front++]); } } void main() { int v; printf("Enter the number of vertices: "); scanf("%d", &n); for (i = 1; i <= n; i++) { queue[i] = 0; visited[i] = 0; } printf("Enter graph data in matrix form: \n"); for (i = 1; i <= n; i++) for (j = 1; j <= n; j++) scanf("%d", &adj[i][j]); printf("Enter the starting vertex: "); scanf("%d", &v); bfs(v); printf("The node which are reachable are: \n"); for (i = 1; i <= n; i++) if (visited[i]) printf("%d\t", i); else printf("BFS is not possible. Not all nodes are reachable"); return 0; }
1. First take the number of nodes in the graph as input and then create an adjacency matrix of size n x n where n is the number of nodes in the graph.
2. Next take the adjacency matrix as input.
3. Take the starting node as input.
4. We then call the bfs function with the starting node as the argument.
5. In the bfs function, we first mark the current node as visited and then we enqueue all the nodes which are adjacent to the current node and are not visited.
6. We then dequeue a node from the queue and call the bfs function with the dequeued node as the argument.
7. We repeat the above steps until the queue is empty.
8. Finally, we print the nodes which are reachable from the starting node.
In this case, we are entering the number of vertices and graph data as input to find the reachables nodes using bfs algorithm.
Enter the number of vertices: 4 Enter graph data in matrix form: 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 Enter the starting vertex: 2 The node which are reachable are: 1 2 3 4
In this approach, we will use an array of linked lists to represent the graph. The array will have the size of n where n is the number of nodes in the graph. The value of the array at index i will be the head of the linked list which will contain all the nodes which are adjacent to node i.
Here is source code of the C program to implement bfs using adjacency list. The C program is successfully compiled and run on a Linux system. The program output is also shown below.
/* * C program to implement bfs using adjacency list */ #include <stdio.h> #include <stdlib.h> struct node { int vertex; struct node *next; }; struct node *createNode(int); struct Graph { int numVertices; struct node **adjLists; int *visited; }; struct Graph *createGraph(int vertices) { struct Graph *graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node *)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) { graph->adjLists[i] = NULL; graph->visited[i] = 0; } return graph; } void addEdge(struct Graph *graph, int src, int dest) { struct node *newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } struct node *createNode(int v) { struct node *newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; } void printGraph(struct Graph *graph) { int v; for (v = 0; v < graph->numVertices; v++) { struct node *temp = graph->adjLists[v]; printf("\n Adjacency list of vertex %d\n ", v); while (temp) { printf("%d -> ", temp->vertex); temp = temp->next; } printf("\n"); } } void bfs(struct Graph *graph, int startVertex) { struct node *queue = NULL; graph->visited[startVertex] = 1; enqueue(&queue, startVertex); while (!isEmpty(queue)) { printQueue(queue); int currentVertex = dequeue(&queue); printf("Visited %d ", currentVertex); struct node *temp = graph->adjLists[currentVertex]; while (temp) { int adjVertex = temp->vertex; if (graph->visited[adjVertex] == 0) { graph->visited[adjVertex] = 1; enqueue(&queue, adjVertex); } temp = temp->next; } } } int isEmpty(struct node *queue) { return queue == NULL; } void enqueue(struct node **queue, int value) { struct node *newNode = createNode(value); if (isEmpty(*queue)) { *queue = newNode; } else { struct node *temp = *queue; while (temp->next) { temp = temp->next; } temp->next = newNode; } } int dequeue(struct node **queue) { int nodeData = (*queue)->vertex; struct node *temp = *queue; *queue = (*queue)->next; free(temp); return nodeData; } void printQueue(struct node *queue) { while (queue) { printf("%d ", queue->vertex); queue = queue->next; } printf("\n"); } int main(void) { struct Graph *graph = createGraph(6); printf("\nWhat do you want to do?\n"); printf("1. Add edge\n"); printf("2. Print graph\n"); printf("3. BFS\n"); printf("4. Exit\n"); int choice; scanf("%d", &choice); while (choice != 4) { if (choice == 1) { int src, dest; printf("Enter source and destination: "); scanf("%d %d", &src, &dest); addEdge(graph, src, dest); } else if (choice == 2) { printGraph(graph); } else if (choice == 3) { int startVertex; printf("Enter starting vertex: "); scanf("%d", &startVertex); bfs(graph, startVertex); } else { printf("Invalid choice\n"); } printf("What do you want to do?\n"); printf("1. Add edge\n"); printf("2. Print graph\n"); printf("3. BFS\n"); printf("4. Exit\n"); scanf("%d", &choice); } return 0; }
1. First create a graph with the number of vertices as the argument.
2. We then create a node for the adjacency list of each vertex.
3. We then add an edge between the source and destination vertices.
4. We then print the graph.
5. We then perform BFS on the graph starting from the starting vertex.
In this case, we are entering the source and destination as input to find the graph using bfs algorithm.
What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 1 Enter source and destination: 0 1 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 1 Enter source and destination: 0 2 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 1 Enter source and destination: 1 2 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 1 Enter source and destination: 2 3 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 2 Adjacency list of vertex 0 2 -> 1 -> Adjacency list of vertex 1 2 -> 0 -> Adjacency list of vertex 2 3 -> 1 -> 0 -> Adjacency list of vertex 3 2 -> Adjacency list of vertex 4 Adjacency list of vertex 5 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 3 Enter starting vertex: 0 0 Visited 0 2 1 Visited 2 1 3 Visited 1 3 Visited 3 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit 4
In this method, we use a queue to store the vertices that are to be visited. We first enqueue the starting vertex and then dequeue it. We then enqueue all the adjacent vertices of the dequeued vertex and mark them as visited. We then dequeue the next vertex and enqueue all its adjacent vertices and so on.
Here is source code of the C program to implement bfs using queue. The C program is successfully compiled and run on a Linux system. The program output is also shown below.
/* * C program to implement bfs using queue */ #include <stdio.h> #include <stdlib.h> struct node { int vertex; struct node *next; }; struct Graph { int numVertices; struct node **adjLists; int *visited; }; struct node *createNode(int v); struct Graph *createGraph(int vertices); void addEdge(struct Graph *graph, int src, int dest); void printGraph(struct Graph *graph); void bfs(struct Graph *graph, int startVertex); int isEmpty(struct node *queue); void enqueue(struct node **queue, int value); int dequeue(struct node **queue); void printQueue(struct node *queue); struct node *createNode(int v) { struct node *newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; } struct Graph *createGraph(int vertices) { struct Graph *graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) { graph->adjLists[i] = NULL; graph->visited[i] = 0; } return graph; } void addEdge(struct Graph *graph, int src, int dest) { // Add edge from src to dest struct node *newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Add edge from dest to src newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } void printGraph(struct Graph *graph) { int v; for (v = 0; v < graph->numVertices; v++) { struct node *temp = graph->adjLists[v]; printf("Adjacency list of vertex %d :", v); while (temp) { printf("%d -> ", temp->vertex); temp = temp->next; } printf("\n"); } } void bfs(struct Graph *graph, int startVertex) { struct node *queue = NULL; graph->visited[startVertex] = 1; enqueue(&queue, startVertex); while (!isEmpty(queue)) { printQueue(queue); int currentVertex = dequeue(&queue); printf("Visited %d ", currentVertex); struct node *temp = graph->adjLists[currentVertex]; while (temp) { int adjVertex = temp->vertex; if (graph->visited[adjVertex] == 0) { graph->visited[adjVertex] = 1; enqueue(&queue, adjVertex); } temp = temp->next; } } } int isEmpty(struct node *queue) { return queue == NULL; } void enqueue(struct node **queue, int value) { struct node *newNode = createNode(value); if (isEmpty(*queue)) { *queue = newNode; } else { struct node *temp = *queue; while (temp->next) { temp = temp->next; } temp->next = newNode; } } int dequeue(struct node **queue) { if (isEmpty(*queue)) { return -1; } else { struct node *temp = *queue; *queue = (*queue)->next; int value = temp->vertex; free(temp); return value; } } void printQueue(struct node *queue) { struct node *temp = queue; while (temp) { printf("%d ", temp->vertex); temp = temp->next; } printf("\n"); } int main(void) { printf("Enter number of vertices: "); int vertices; scanf("%d", &vertices); struct Graph *graph = createGraph(vertices); int choice; do { printf("\nWhat do you want to do? \n"); printf(" 1. Add edge\n 2. Print graph\n 3. BFS\n 4. Exit\n"); printf("Enter your choice: "); scanf("%d", &choice); switch (choice) { case 1: printf("Enter source and destination: "); int src, dest; scanf("%d %d", &src, &dest); addEdge(graph, src, dest); break; case 2: printGraph(graph); break; case 3: printf("Enter starting vertex: "); int startVertex; scanf("%d", &startVertex); bfs(graph, startVertex); break; case 4: break; default: printf("Invalid choice"); } } while (choice != 4); return 0; }
The code is similar to the previous one. The only difference is that we use a queue to store the vertices that are to be visited. We first enqueue the starting vertex and then dequeue it. We then enqueue all the adjacent vertices of the dequeued vertex and mark them as visited. We then dequeue the next vertex and enqueue all its adjacent vertices and so on. We continue this process until the queue is empty.
In this case, we are entering the source and destination as input to find the graph using bfs algorithm.
Enter number of vertices: 4 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 0 1 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 0 4 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 1 2 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 1 3 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 1 4 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 2 3 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 1 Enter source and destination: 3 4 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 2 Adjacency list of vertex 0 :4 -> 1 -> Adjacency list of vertex 1 :4 -> 3 -> 2 -> 0 -> Adjacency list of vertex 2 :3 -> 1 -> Adjacency list of vertex 3 :4 -> 2 -> 1 -> What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 3 Enter starting vertex: 0 0 Visited 0 4 1 Visited 4 1 3 Visited 1 3 2 Visited 3 2 Visited 2 What do you want to do? 1. Add edge 2. Print graph 3. BFS 4. Exit Enter your choice: 4
To practice programs on every topic in C, please visit “Programming Examples in C”, “Data Structures in C” and “Algorithms in C”.
If you find any mistake above, kindly email to [email protected]- Check C Books
- Apply for Computer Science Internship
- Apply for C Internship
- Practice BCA MCQs
- Practice Computer Science MCQs
