This set of Surveying Puzzles focuses on “Area Calculation – Area by Double Meridian Distances”.
1. Double meridian distance of a line is equal to __________
a) Sum of parallel distances
b) Sum of perpendicular distances
c) Sum of total areas
d) Sum of meridian distances
View Answer
Explanation: The double meridian distance of a line is equal to the sum of the meridian distances of the two extremities, which is useful for the determination of the required area of the plot.
2. Which of the following area calculation methods is mostly used?
a) Area by double meridian
b) Area by co-ordinates
c) Area by planimeter
d) Area by Simpson’s rule
View Answer
Explanation: Area by double mean distances involves more methods of obtaining the area, which actually increases the accuracy of the output. Each method is having its own importance which can be sorted out based on the inputs available.
3. The double parallel distance can be given as __________
a) Sum of vertical distances
b) Sum of perpendicular distances
c) Sum of parallel distances
d) Area of parallel distances
View Answer
Explanation: The double parallel distance for a line can be given as sum of the parallel distances of its ends. The principles of finding area by D.M. D. method and D.P.D. method are identical.
4. Which of the following indicates the purpose of D.P.D?
a) Checking area computed by D.P.D
b) Checking area computed by D.M.D
c) Checking area computed by perpendiculars
d) Checking area computed by parallels
View Answer
Explanation: The D.P.D method is employed for checking the area computed by D.M.D method. It is an independent area and has its own set of rules but some principles are identical.
5. Which of the following describes the double meridian distance?
a) Sum of latitudes
b) Sum of horizontal distances
c) Sum of parallel distances
d) Sum of meridian distances
View Answer
Explanation: Double meridian distance of a line is equal to sum of the meridian distances of the two extremities. It is represented by the symbol M. The area calculated by double meridian distance can be having accuracy in its output.
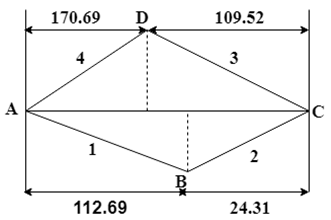
6. Calculate the area of the figure by using the data provided. L1 = 92.69 m, L2 = 248.96 m, L3 = 146.31m, L4 = 157.43 m.
a) 29283.46 sq. m
b) 29823.46 sq. m
c) 29328.64 sq. m
d) 29238.64 sq. m
View Answer
Explanation: From the figure, it can be observed that it consist four triangles so the total are can be given as the summation of the area of triangles.
A = 1⁄2(D1*L1) + 1⁄2(D2*L2) + 1⁄2(D3*L3) + 1⁄2(D4*L4)
= 1⁄2(112.69*92.69) + 1⁄2(242.96*24.31) + 1⁄2(146.31*170.69) + 1⁄2(157.43*109.52)
= 5222.61 + 2953.17 + 12486.82 + 8620.86 = 29283.46 sq. m.
7. Find the value of M2 if D1 = 24.86 m, D2 = 17.65 m.
a) 76.37 m
b) 67.37 m
c) 76.73 m
d) 37.76 m
View Answer
Explanation: The value of M2 can calculated by M2 = M1 + D1 + D2. But we already know that M1 = D1. So, on substitution, we get
M2 = 24.86 + 24.86 + 17.65 = 67.37 m.
8. Find the meridian distance if m1 = 32.76, and D2 = 44.56 m.
a) 71.24 m
b) 17.24 m
c) 17.42 m
d) 71.42 m
View Answer
Explanation: Meridian distance can be calculated by m2 = m1 + D1/2 + D2/2. On substitution we get,
m2 = 32.76 + 32.76/2 + 44.56/2
m2 = 71.42 m.
9. Find the area of a triangle if latitude distance is given as 209.96 m and meridian distance is 5.78 m.
a) 1213.86 sq. m
b) 1231.68 sq. m
c) 1213.68 sq. m
d) 1123.68 sq. m
View Answer
Explanation: If the latitude and meridian distance are given then the area of a triangle can be calculated by the product of both i.e., Area of triangle = latitude * meridian distance = 209.96 * 5.78 = 1213.68 sq. m.
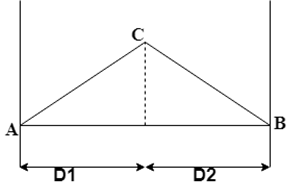
10. Find the area of the figure by double distances, if L1 = 13.99 m and L2 = 66.54 m.
a) 2247.17 sq. m
b) 2274.17 sq. m
c) 2274.71 sq. m
d) 2247.71 sq. m
View Answer
Explanation: The formula for area by double distances can be given as
A = 1⁄2 (M1*L1+ M2*L2). We know that, M1 = D1 = 24.56 m and M2 = M1 + D1 + D2 = 24.56 + 24.56 + 13.26 = 62.38 m. On substitution, we get
A = 1⁄2(24.56*13.99 + 62.38 * 66.54) = 2247.17 sq. m.
Sanfoundry Global Education & Learning Series – Surveying.
To practice all Puzzles on Surveying, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Civil Engineering Internship
- Practice Civil Engineering MCQs
- Check Surveying Books
- Check Civil Engineering Books
