This set of Statistical Quality Control Multiple Choice Questions & Answers (MCQs) focuses on “Gauge and Measurement System Capability Studies – 3”.
1. SNR represents __________
a) Sign to noise ratio
b) Sample to nonconforming ratio
c) Size to noise ratio
d) Signal to noise ratio
View Answer
Explanation: A measure of measurement system adequacy is defined by AIAG, which is called SNR or signal to noise ratio. It is used to check the satisfactoriness of the measurement system.
2. SNR is equal to _________
a) \(\sqrt{\frac{2ρ_p}{1-ρ_p}}\)
b) \(\sqrt{\frac{3ρ_p}{1-ρ_p}}\)
c) \(\sqrt{\frac{ρ_p}{1-ρ_p}}\)
d) \(\frac{2ρ_p}{1-ρ_p}\)
View Answer
Explanation: SNR is the measure of measurement system adequacy. It uses the gauge capability ratio ρp. It is expressed as,
SNR=\(\sqrt{\frac{2ρ_p}{1-ρ_p}}\)
3. What is the correct definition of SNR?
a) The number of signals for 30 noise indications on control chart
b) The number of signals for single noise indication on control chart
c) The number of signals with no noise from the measurements
d) The number of distinct levels or categories that can be reliably obtained from the measurements
View Answer
Explanation: SNR is defined by AIAG as the number of distinct levels or categories that can be reliably obtained from the measurement.
4. If the estimate of pp is 0.9214, what will be the estimate of SNR?
a) 4.84
b) 6.87
c) 9.12
d) 2.13
View Answer
Explanation: We know that,
SNR=\(\sqrt{\frac{2ρ_p}{1-ρ_p}}\)
By putting the value of the estimate of ρp we get SNR estimate = 4.84.
5. Which of these is not one of the gauge capability ratios?
a) SNR
b) Cp
c) ρM
d) ρp
View Answer
Explanation: SNR, ρp and ρM are some examples of the gauge capability ratios, which are used to check the adequacy of the measurement system used.
6. What is the full-form of DR in the context of gauge capability?
a) Decrease rate
b) Direction ratios
c) Discrimination ratios
d) Dimension rates
View Answer
Explanation: Like the other gauge capability ratios like SNR, ρp, and ρM; DR is also a measure of gauge capability. Its full-form is known as discrimination ratio.
7. What is the value of DR?
a) DR=\(\frac{1-2ρ_p}{1+ρ_p}\)
b) DR=\(\frac{1+ρ_p}{1-ρ_p}\)
c) DR=\(\frac{1+2ρ_p}{1-ρ_p}\)
d) DR=\(\frac{1-ρ_p}{1+ρ_p}\)
View Answer
Explanation: The value of the discrimination ratio, which is used as a measure of adequacy of a measurement system, and which uses the ratio ρp, is used to evaluate the gauge capability. It is expressed as,
DR=\(\frac{1-ρ_p}{1+ρ_p}\)
8. For a measurement system ρp=0.8914. What will be the value of DR for that?
a) 17.416
b) 0.0571
c) 24.46
d) 0.0652
View Answer
Explanation: We know that,
DR=\(\frac{1-ρ_p}{1+ρ_p}\)
Putting the values, we get DR=17.416.
9. For a gauge to be capable, generally DR must be greater than ___________
a) 1
b) 0.4
c) 0.1
d) 4
View Answer
Explanation: It is generally stated that the DR for a capable gauge is, generally having a value higher than 4. This means for a gauge to be capable, the DR must exceed 4.
10. Which of these tells about the inherent variability of the gauge?
a) Accuracy
b) Precision
c) DR ratio
d) SNR
View Answer
Explanation: Precision of a measurement system can be a measure of the inherent variability of the gauge. This is because the inherent variability moves the output of a gauge strongly to one direction or to a point.
11. The picture indicates gauge measurements where the dark circle is true value and the dots as observed value. This picture shows _____
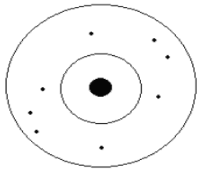
a) More accuracy, less precision
b) Neither accuracy nor precision
c) More precision, less accuracy
d) High accuracy and precision
View Answer
Explanation: The average of the observed values is almost equal to the true value. So from the definition of accuracy, we can say this gauge is more accurate than precise.
12. The standard model for a gauge R & R study is also called ____________
a) Random effects model analysis of variance
b) Continuous effects model analysis of variance
c) Discrete effects model analysis of variance
d) Attribute effects model analysis of variance
View Answer
Explanation: The standard model for a gauge R & R study is also called a random effects model analysis of variance. It is generally used while calculating the gauge capability.
13. The more the gauge capability, the more are the ____________
a) Tolerances
b) Specifications
c) Chances of rejection
d) Chances of no error in measurements
View Answer
Explanation: The gauge capability represents the ability of gauge to measure the dimension or unit correctly. The more is the gauge capability, the more are the chances of no error in measurements.
14. Even if the instantaneous value measured for a dimension by a gauge is not equal to the true value, but the gauge can still be accurate.
a) True
b) False
View Answer
Explanation: The accuracy of a gauge refers to the ability of the instrument to measure the true value correctly, on average. So even if the instantaneous value by a gauge is not equal to the true value, but average of it is almost equal to the true value, the gauge is accurate.
15. An equipment can be more precise but not accurate at the same time.
a) True
b) False
View Answer
Explanation: Accuracy refers to the ability of the instrument to measure the true value correctly on average, but precision is a measure of inherent variability in the measurement system, so both can be present, even in the absence of either one of them.
Sanfoundry Global Education & Learning Series – Statistical Quality Control.
To practice all areas of Statistical Quality Control, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Statistical Quality Control Books
- Check Mechanical Engineering Books
