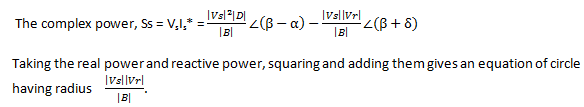This set of Power Systems Multiple Choice Questions & Answers (MCQs) focuses on “Symmetrical Component Transformation – 1”.
1. The receiving end active power for a short transmission line is (where the angles have their usual meanings)
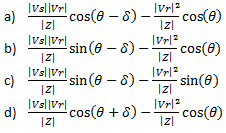
View Answer
Explanation: Receiving end active power for a short transmission line is
2. The receiving end reactive power for a short transmission line is (where the angles have their usual meanings)
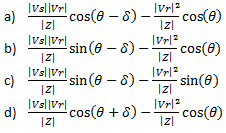
View Answer
Explanation: Receiving end reactive power for a short transmission line is
3. The sending end active power for a 20 km transmission line with Vs as the sending end voltage and Vr as receiving end voltage, can be given by most appropriately
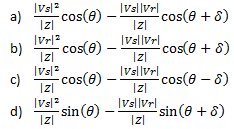
View Answer
Explanation: The sending end active power is
4. The sending end reactive power for a 20 km transmission line with Vs as the sending end voltage and Vr as receiving end voltage, can be given by most appropriately
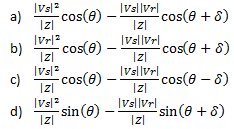
View Answer
Explanation: The sending end reactive power is
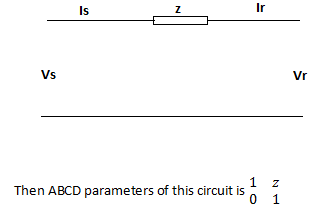
5. The simplified ABCD representation of a 40 km transmission line is best given as
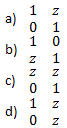
View Answer
Explanation: From the given length, it is a short TL. Hence,
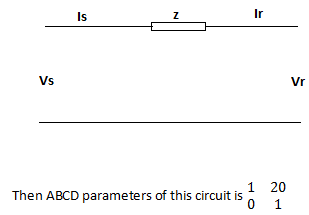
6. For a 35 km transmission line having a lumped impedance of the line as 20 ohms, is required to be shown in the ABCD form, it is given as
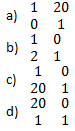
View Answer
Explanation: From the given length, it is a short TL. Hence,
7. If it is tried to represent the active and reactive power on a circle, then the radius would be
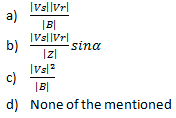
View Answer
Explanation:
8. The maximum power delivered to the load for short transmission line is at
a) β=α
b) β>α
c) β=δ
d) β>δ
View Answer
Explanation: Maximum power occurs for β=δ.
9. The maximum real active power delivered to the load is defined most accurately by
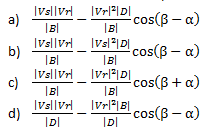
View Answer
Explanation: The maximum real active power delivered to the load is
10. For a given power system, its zero and maximum regulation will occur at the impedance angle of
a) 45
b) 90
c) 0
d) 60
View Answer
Explanation: At θ=45°, ZVR and maximum VR coincide.
11. The charging currents due to shunt admittance can be neglected for ______ transmission line?
a) short
b) long
c) medium
d) all of the mentioned
View Answer
Explanation: The shun admittance for lines more than 100 km become very prominent and can not be neglected.
12. The transmission line equations are given by the below set of equations based on the line diagram as given. Identify the missing term marked as ’?’.
Vs = ?*Vr+B*Ir
Is = C*Vr+D*Ir
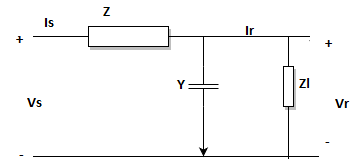
a) 1+YZ
b) Z
c) Y
d) 1
View Answer
Explanation: Using KVL to the line diagram,
Vs = (1+YZ)*Vr+Z*Ir
Is = Y*Vr+Ir.
13. The transmission line equations are given by the below set of equations based on the line diagram as given. Identify the missing term marked as ’?’.
Vs = A*Vr+?*Ir
Is = C*Vr+D*Ir
a) 1+YZ
b) Z
c) Y
d) 1
View Answer
Explanation: Using KVL to the line diagram,
Vs = (1+YZ)*Vr+Z*Ir
Is = Y*Vr+Ir.
14. The transmission line equations are given by the below set of equations based on the line diagram as given. Identify the missing term marked as ’?’.
Vs = A*Vr+B*Ir
Is = ?*Vr+D*Ir
a) 1+YZ
b) Z
c) Y
d) 1
View Answer
Explanation: Using KVL to the line diagram,
Vs = (1+YZ)*Vr+Z*Ir
Is = Y*Vr+Ir.
15. The transmission line equations are given by the below set of equations based on the line diagram as given. Identify the missing term marked as ’?’.
Vs = A*Vr+B*Ir
Is = C*Vr+?*Ir
a) 1+YZ
b) Z
c) Y
d) 1
View Answer
Explanation: Using KVL to the line diagram,
Vs = (1+YZ)*Vr+Z*Ir
Is = Y*Vr+Ir.
Sanfoundry Global Education & Learning Series – Power Systems.
To practice all areas of Power Systems, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Electrical & Electronics Engineering Internship
- Apply for Electrical Engineering Internship
- Check Electrical Engineering Books
- Practice Electrical & Electronics Engineering MCQs
- Practice Electrical Engineering MCQs
