This set of Power Electronics Multiple Choice Questions & Answers (MCQs) focuses on “PWM Inverters-1”.
1. In the single-pulse width modulation method, the output voltage waveform is symmetrical about __________
a) π
b) 2π
c) π/2
d) π/4
View Answer
Explanation: The waveform is a positive in the first half cycle and symmetrical about π/2 in the first half.
2. In the single-pulse width modulation method, the output voltage waveform is symmetrical about ____________ in the negative half cycle.
a) 2π
b) 3π/2
c) π/2
d) 3π/4
View Answer
Explanation: In the negative half the wave is symmetrical about 3π/2.
3. The shape of the output voltage waveform in a single PWM is
a) square wave
b) triangular wave
c) quasi-square wave
d) sine wave
View Answer
Explanation: Positive and the negative half cycles of the output voltage are symmetrical about π/2 and 3π/2 respectively. The shape of the waveform obtained is called as quasi-square wave.
4. In the single-pulse width modulation method, the Fourier coefficient bn is given by
a) (Vs/π) [ sin(nπ/2) sin(nd) ].
b) 0
c) (4Vs/nπ) [sin(nπ/2) sin(nd)].
d) (2Vs/nπ) [sin(nπ/2) sin(nd)].
View Answer
Explanation: The Fourier analysis is as under:
bn = (2/π) ∫ Vs sin nωt .d(ωt) , Where the integration would run from (π/2 + d) to (π/2 – d)
2d is the width of the pulse.
5. In the single-pulse width modulation method, the Fourier coefficient an is given by
a) (Vs/π) [ cos(nπ/2) cos(nd) ].
b) 0
c) (4Vs/nπ) [sin(nπ/2) sin(nd)].
d) (2Vs/nπ) [sin(nπ/2) sin(nd)].
View Answer
Explanation: As the positive and the negative half cycles are identical the coefficient an = 0.
6. In the single-pulse width modulation method, when the pulse width of 2d is equal to its maximum value of π radians, then the fundamental component of output voltage is given by
a) Vs
b) 4Vs/π
c) 0
d) 2Vs/π
View Answer
Explanation: The Fourier representation of the output voltage is given by
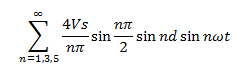
Put 2d = π & n = 1.
7. In case of a single-pulse width modulation with the pulse width = 2d, the peak value of the fundamental component of voltage is given by the expression
a) 4Vs/π
b) Vs
c) (4Vs/π) sin 2d
d) (4Vs/π) sin d
View Answer
Explanation: For the fundamental component put n = 1.
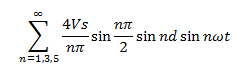
Vo = (4Vs/π) sin (d) sin (ωt)
Hence the peak value is (4Vs/π) sin d.
8. In case of a single-pulse width modulation with the pulse width = 2d, to eliminate the nth harmonic from the output voltage
a) d = π
b) 2d = π
c) nd = π
d) nd = 2π
View Answer
Explanation: To eliminate, the nth harmonic, nd is made equal to π radians, or d = π/n.
From the below expression,
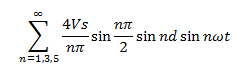
when nd = π. sin nd = 0 hence, that output voltage harmonic is eliminated.
9. Find the peak value of the fundamental component of voltage with a pulse width of 2d = 90 and Vs = 240 V for single-pulse modulation in a full wave bridge inverter.
a) 305 V
b) 216 V
c) 0 V
d) 610 V
View Answer
Explanation: The peak value of the fundamental component of voltage is given by (4Vs/π) sin d.
10. In case of a single-pulse width modulation with the pulse width = 2d, to eliminate the 3rd harmonic from the output voltage waveform, the value of the pulse width (2d) must be
a) 0°
b) 60°
c) 120°
d) 180°
View Answer
Explanation: To eliminate the nth harmonic, nd = π.
Therefore, d = π/n = π/3 = 60°
Hence, 2d = 120°.
Sanfoundry Global Education & Learning Series – Power Electronics.
To practice all areas of Power Electronics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
