This set of Powder Metallurgy Questions and Answers for Campus interviews focuses on “Sintering Mechanism – 3”.
1. Nabarro and Herring supported ________ as the dominant mechanism in sintering.
a) Evaporation-condensation
b) Viscous flow
c) Diffusion
d) Recrystallization
View Answer
Explanation: According to Nabarro and Herring diffusion is the dominant mechanism in sintering because surface stresses change the concentration of the vacancies near the surface and create vacancy gradients that favor diffusion.
2. ___________ are structural arrangement of dislocations and are not perfect sinks.
a) Pores
b) Grain boundaries
c) Vacancies
d) Necks
View Answer
Explanation: Originally grain boundaries were thought to be pipes that allowed vacancies to reach the surface. Later the concept that the grain boundaries were perfect sinks for vacancies was developed which showed that the diffusion path was dependent on the distance between the pore and grain boundary and not the size. However, it is now considered that grain boundaries are structural arrangement of dislocations and are not perfect sinks. The effectiveness of grain boundaries as a source of atoms or sinks for vacancies is dependent on the mobility of dislocations.
3. The expression for viscous flow mechanism proposed by Frenkel is given by ________
a) \(\frac{x^2}{a}=\frac{3\gamma \eta}{2t}\)
b) \(\frac{x^3}{a}=\frac{3\gamma t}{2\eta}\)
c) \(\frac{x^2}{a}=\frac{3\gamma}{2\eta}\)
d) \(\frac{x^2}{a}=\frac{3\gamma t}{2\eta}\)
View Answer
Explanation: The expression for viscous flow mechanism proposed by Frenkel is important in the sintering of glass and it is given by \(\frac{x^2}{a}=\frac{3\gamma t}{2\eta}\) where, x=neck radius, a=radius of particle, γ=surface tension, η=glass viscosity and t=sintering time.
4. Which of the following mechanisms operate during sintering, according to Bal’shin theory?
a) Particle re-arrangement, particle shape change, and grain shrinkage
b) Particle shape change, particle size change, and grain growth
c) Particle re-arrangement, particle shape change, and grain growth
d) Particle re-arrangement and grain growth
View Answer
Explanation: Bal’shin proposed that following mechanisms are occurring during sintering- (1) Particle re-arrangement, (2) Particle shape change, and (3) Grain growth. According to Bal’shin, although several forces are acting during sintering plastic deformation is the major mechanism leading to densification.
5. The equation for coefficient of viscosity as proposed by Frenkel, is given by ________
a) η=\(\frac{k^2T}{D\Omega}\)
b) η=\(\frac{kT}{D\Omega}\)
c) η=\(\frac{kT}{Dx}\)
d) η=\(\frac{kT}{Da}\)
View Answer
Explanation: Frenkel was the first to make use of a two-sphere model to develop rate kinetics for sintering. Thus, the equation for coefficient of viscosity as proposed by Frenkel, is given by η=\(\frac{kT}{D\Omega}\) where k=Boltzmann constant, T=absolute temperature, D=self-diffusion coefficient, and Ω=atomic volume.
6. Bulk flow of material by movement of dislocations is a possible mechanism for densification during sintering only if the two conditions are met.
a) True
b) False
View Answer
Explanation: Bulk flow of material by movement of dislocations has been proposed as a possible mechanism for densification during sintering. However, the following two conditions must be met- (1) movement of dislocation in the neck region under shear stresses, and (2) generation of new dislocations by surface tension forces.
7. Which of the following is the expression for plastic flow as the driving force for sintering?
a) \(\frac{ds}{dt}=A\sigma^{3n}e^{\frac{Q_c}{RT}}\)
b) \(\frac{ds}{dt}=A\sigma^{2n}e^{\frac{Q_c}{RT}}\)
c) \(\frac{ds}{dt}=A\sigma^{n}e^{\frac{Q_cR}{T}}\)
d) \(\frac{ds}{dt}=A\sigma^{n}e^{\frac{Q_c}{RT}}\)
View Answer
Explanation: Lenel and Ansell supported plastic flow as the driving force for sintering and derived a sintering rate expression \(\frac{ds}{dt}=A\sigma^{n}e^{\frac{Q_c}{RT}}\) where, A=constant, σ=stress, n=stress exponent, Qc=activation energy for creep, R=ideal gas constant, and \(\frac{ds}{dt}\)=creep rate.
8. At equilibrium, the relation between dihedral angle and surface energy is represented by the equation ______
a) cos\(\frac{\theta}{2}=-\frac{\gamma_{sv}}{\gamma_{ss}}\)
b) cos\(\frac{\theta}{2}=\frac{\gamma_{sv}}{\gamma_{ss}}\)
c) cos\(\frac{\theta}{2}=\frac{\gamma_{ss}}{\gamma_{sv}}\)
d) cos\(\frac{\theta}{2}=-\frac{\gamma_{ss}}{\gamma_{sv}}\)
View Answer
Explanation: The dihedral angle θ is a measure of surface and pore geometry and at equilibrium is related to surface energy by the equation cos\(\frac{\theta}{2}=\frac{\gamma_{ss}}{\gamma_{sv}}\) where, γss and γsv are the surface energies of the solid-solid and solid-vapor interfaces respectively. If the dihedral angle is less than the equilibrium dihedral angle, sintering may continue.
9. Entrapment of gas within the pores is an important reason for not achieving theoretical density in practice during sintering.
a) True
b) False
View Answer
Explanation: Gas entrapment with in the pores does not allow us to achieve theoretical density in practice during sintering, this is because, during the final stage of sintering, pores become isolated and any gas remaining becomes trapped and thus shrinkage will be opposed by the presence of the gas in the pore. The other reasons for not achieving theoretical density in practice are presence of agglomeration, poor packing, and non-uniform particle size.
10. The equilibrium pore pressure is given by Pp= ________
a) Patm-2γsv/r
b) Patm+2γsv/r
c) Patm+2γss/r
d) Patm+2γsv/x
View Answer
Explanation: The equilibrium pore pressure is given by Pp for an isolated spherical pore is given by Patm+2γsv/r where, Patm is the atmospheric pressure, r is the pore radius, and γsv is the surface energy of solid-vapor interface. Thus, on increasing Patm (as in hot isostatic pressing) will decrease the pore radius.
11. The above diagram represents criteria for pore removal during sintering.
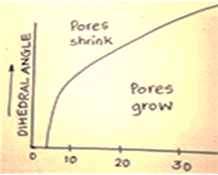
a) True
b) False
View Answer
Explanation: There is a critical pore coordination number Np, that is the number of particles surrounding which is related to \(\frac{\gamma_{ss}}{\gamma_{sv}}\) above which the pore is stable while below which the pore is unstable and disappears.
12. Coble developed rate equations for three stage sintering assuming the compact to be made of packed spheres and in the final stage form interlocking ___________
a) Tetrakaioctahedrons
b) Tetrakaidecahedrons
c) Tetracontagons
d) Tetrakaitetrahedrons
View Answer
Explanation: Coble developed rate equations for three stage sintering assuming the compact to be made of packed spheres and in the final stage form interlocking tetrakaidecahedrons. According to Coble, the necks form in the initial stage of sintering but the distance between the particle centers remain constant. During the intermediate stage, necks grow, shrinkage may occur and grain growth may occur. During the third stage, the pores become isolated, the pores being considered as spheres at the grain boundaries.
Sanfoundry Global Education & Learning Series – Powder Metallurgy.
To practice all areas of Powder Metallurgy for Campus Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Mechanical Engineering MCQs
- Practice Metallurgical Engineering MCQs
- Check Metallurgical Engineering Books
- Check Powder Metallurgy Books
- Check Mechanical Engineering Books
